题目链接：AcWing 291. 蒙德里安的梦想
问题描述

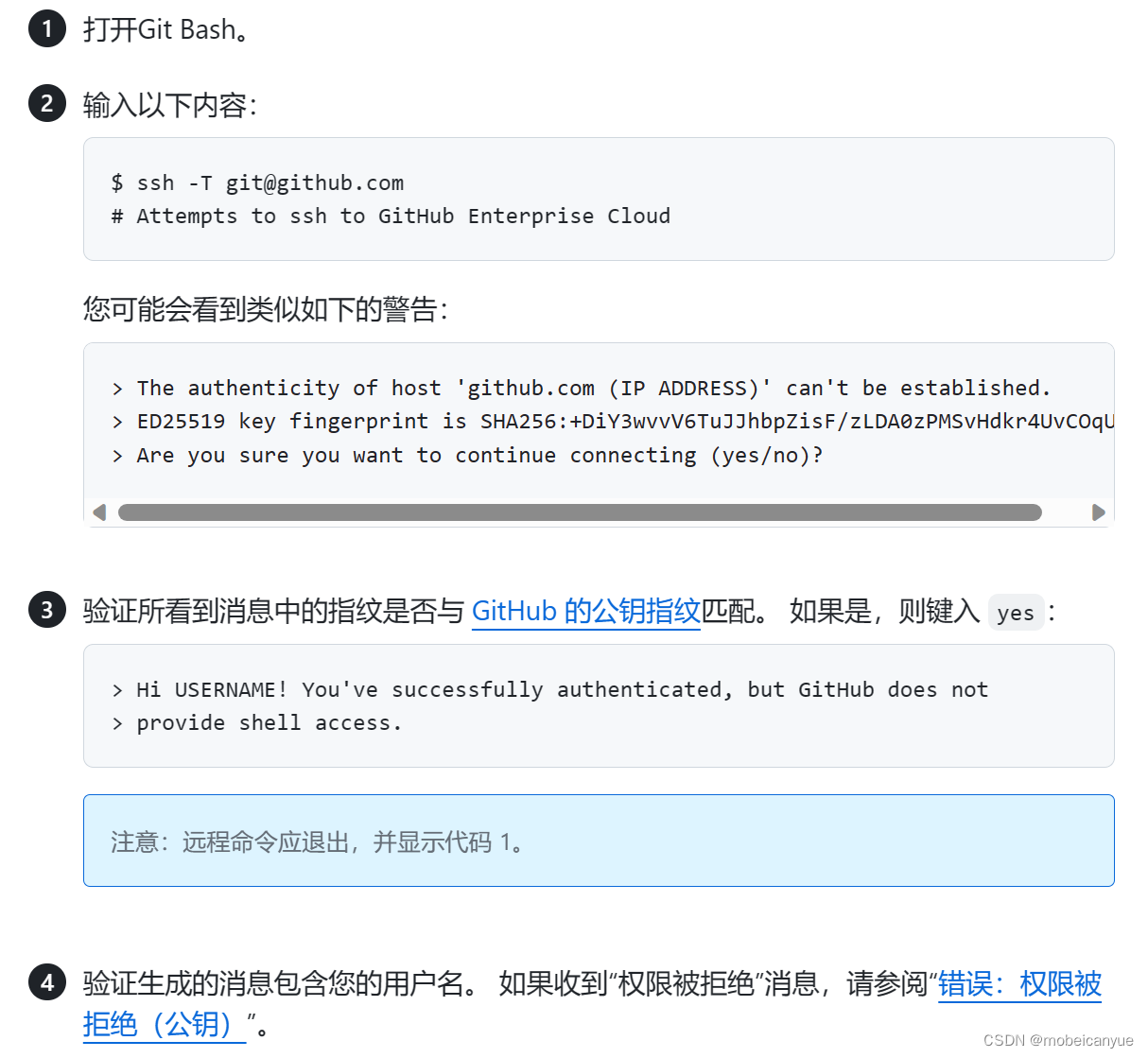
分析

这是一道经典的状态压缩DP问题，横着或者竖着排列1*2的方块
可以发现，横(竖)着的合法排列方案数就是问题的解，因为横(竖)着的合法排列后竖(横)着的只有一种排列方法,
这里我们考虑求横向的排列方案数
状态表示:
用f[i][j]来表示考虑第i行的排列为j时的方案数，j的2进制就代表了排列方式，例如010就代表第二行放一块1*2的小方块

状态转移：
f[i][j]从f[i-1][k](第i-1列)转移而来
需要考虑转移是否合法
(1)首先如果第i-1列的第w行放置了一个小方块，小方块会延申到第i列，那么第i列的第w行就被用了，就不能排放小方块了
所以j&k==0来保证没有冲突
(2)其次，我们要保证横着排列后能让竖着排列也合法，也就是竖着的连续空位置不能是奇数个，在给定行数的情况下这个可以通过预处理提前求出来
考虑这两个条件，f[i][j]+=f[i-1][k]

代码如下

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=12,M=1<<12;
ll f[N][M];//f[i][j]表示当前放置小方块方案为j时的方案数
bool st[M];
bool find(int n,int x){
    int cnt=0;
    for(int i=0;i<n;i++)
        if((x>>i)&1){
            if(cnt&1) return false;
            cnt=0;
        }
        else cnt++;
    if(cnt&1) return false;
    return true;
}
int main(){
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        if(n==0&&m==0) break;
        memset(f,0,sizeof f);
        for(int i=0;i<1<<n;i++) st[i]=find(n,i);
        f[0][0]=1;
        for(int i=1;i<=m;i++)
            for(int j=0;j<(1<<n);j++)
                for(int k=0;k<(1<<n);k++)
                    if((j&k)==0&&st[j|k]) f[i][j]+=f[i-1][k];
        cout<<f[m][0]<<endl;
    }
    return 0;
}