Leetcode -872.叶子相似的树

题目：请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。
如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

示例 1：

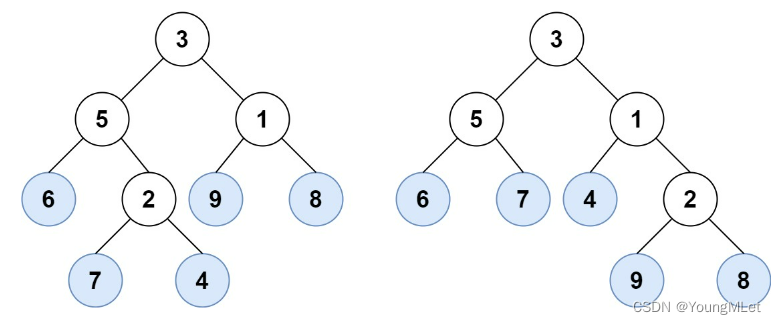
输入：root1 = [3, 5, 1, 6, 2, 9, 8, null, null, 7, 4], root2 = [3, 5, 1, 6, 7, 4, 2, null, null, null, null, null, null, 9, 8]
输出：true

示例 2：

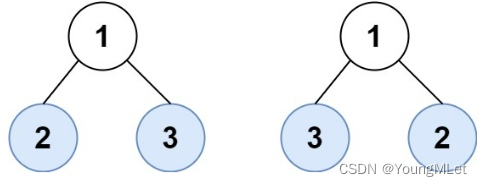
输入：root1 = [1, 2, 3], root2 = [1, 3, 2]
输出：false

提示：
给定的两棵树结点数在 [1, 200] 范围内
给定的两棵树上的值在 [0, 200] 范围内

思路：创建两个数组 a1，a2 分别存放两棵树的叶子节点，最后依次比较两个数组的值是否相等，相等返回 true，否则返回 false；

		void dfs(struct TreeNode* root, int* a, int* Size)
		{
		    if (root == NULL)
		        return;
		
		    //判断是否是叶子节点
		    if (root->left == NULL && root->right == NULL)
		    {
		        a[(*Size)++] = root->val;
		        return;
		    }
		
		    dfs(root->left, a, Size);
		    dfs(root->right, a, Size);
		}
		
		
		bool leafSimilar(struct TreeNode* root1, struct TreeNode* root2)
		{
		    //创建两个数组，分别存放两棵树的叶子的值
		    int a1[200];
		    int a2[200];
		    int Size1 = 0, Size2 = 0;
		
		    dfs(root1, a1, &Size1);
		    dfs(root2, a2, &Size2);
		
		    //如果两棵树的叶子的长度不一样，返回false
		    if (Size1 != Size2)
		        return false;
		
		    //遍历两个数组，比较对应的叶子节点的值是否相等，不相等就返回false
		    for (int i = 0; i < Size1; i++)
		    {
		        if (a1[i] != a2[i])
		            return false;
		    }
		
		    //最后到这里说明相等，返回true
		    return true;
		}

Leetcode -993.二叉树的堂兄弟节点

题目：在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k + 1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：

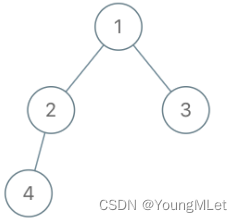
输入：root = [1, 2, 3, 4], x = 4, y = 3
输出：false

示例 2：

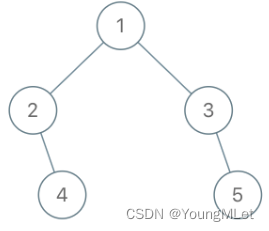
输入：root = [1, 2, 3, null, 4, null, 5], x = 5, y = 4
输出：true

示例 3：

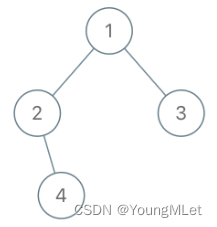
输入：root = [1, 2, 3, null, 4], x = 2, y = 3
输出：false

提示：
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

思路：定义 x 和 y 的 target ，depth ，parent 和 found，分别是 x 或 y 的值；x 或 y 节点所在树的深度；x 或 y 的父节点（假设根节点的父节点是NULL）；x 或 y 的查找情况；然后递归树，如果找到值为 x 或 y 的节点就更新 x 或 y 的情况；

		//分别定义 x 的值：x_target；x 所在节点的深度：x_depth；x 节点的父节点：x_parent；是否找到 x 节点：x_found
		int x_target;
		int x_depth;
		struct TreeNode* x_parent;
		bool x_found;
		
		int y_target;
		int y_depth;
		struct TreeNode* y_parent;
		bool y_found;
		
		
		void dfs(struct TreeNode* root, int depth, struct TreeNode* parent)
		{
		    if (root == NULL)
		        return;
		
		    //如果找到值为 x 的节点，就更新 x 的父节点、深度、查找情况
		    if (root->val == x_target)
		    {
		        x_parent = parent;
		        x_depth = depth;
		        x_found = true;
		    }
		
		    //如果找到值为 y 的节点，就更新 y 的父节点、深度、查找情况
		    if (root->val == y_target)
		    {
		        y_parent = parent;
		        y_depth = depth;
		        y_found = true;
		    }
		
		    // 如果两个的查找情况都为 true，提前返回
		    if (x_found && y_found)
		        return;
		
		    //递归其左子树，当前深度加一，下一个节点的父节点
		    dfs(root->left, depth + 1, root);
		
		    // 如果两个的查找情况都为 true，提前返回
		    if (x_found && y_found)
		        return;
		
		    //递归其右子树，当前深度加一，下一个节点的父节点
		    dfs(root->right, depth + 1, root);
		}
		
		
		bool isCousins(struct TreeNode* root, int x, int y)
		{
		    //初始化
		    x_target = x;
		    y_target = y;
		
		    x_found = false;
		    y_found = false;
		
		    //三个参数分别为根节点，深度，当前节点的父节点（假设第一个节点的父节点为NULL）
		    dfs(root, 0, NULL);
		
		    //最后判断 x 和 y 节点的深度是否相等，并判断它们的父节点是否相同
		    return x_depth == y_depth && x_parent != y_parent;
		}