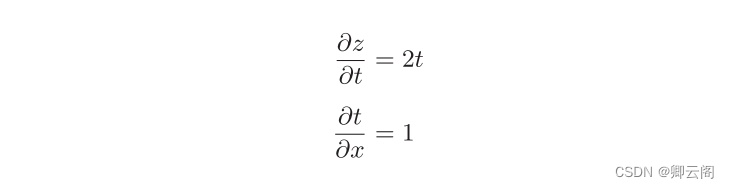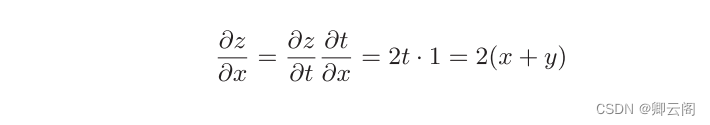🌞欢迎来到深度学习的世界
🌈博客主页:卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创!
🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢!
目录
5.1 计算图
5.2 链式法则
5.3 反向传播
5.5 激活函数层的实现
5.6 Affine/Softmax层的实现
5.7 误差反向传播法的实现
5.1 计算图
5.1.1 用计算图求解
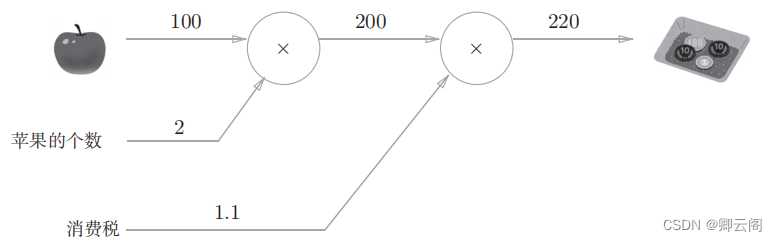
问题1 :太郎在超市买了 2 个 100 日元一个的苹果,消费税是 10% ,请计算支付金额。
从这个计算图的结果可知,答案为220日元。
问题2 :太郎在超市买了 2 个苹果、 3 个橘子。其中,苹果每个 100 日元, 橘子每个150 日元。消费税是 10% ,请计算支付金额。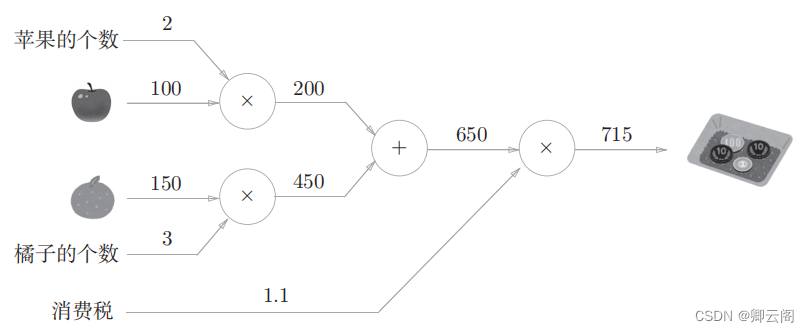 这个问题中新增了加法节点“ + ”,用来合计苹果和橘子的金额。构建了计算图后,从左向右计算。答案为715 日元。
这个问题中新增了加法节点“ + ”,用来合计苹果和橘子的金额。构建了计算图后,从左向右计算。答案为715 日元。综上,用计算图解题的情况下,需要按如下流程进行。
1. 构建计算图。2. 在计算图上,从左向右进行计算。这里的第 2 歩“从左向右进行计算”是一种正方向上的传播,简称为 正向传播(forward propagation )。正向传播是从计算图出发点到结束点的传播。 既然有正向传播这个名称,当然也可以考虑反向(从图上看的话,就是从右向左)的传播。实际上,这种传播称为反向传播 (backward propagation )。反向传播将在接下来的导数计算中发挥重要作用。5.1.2 局部计算
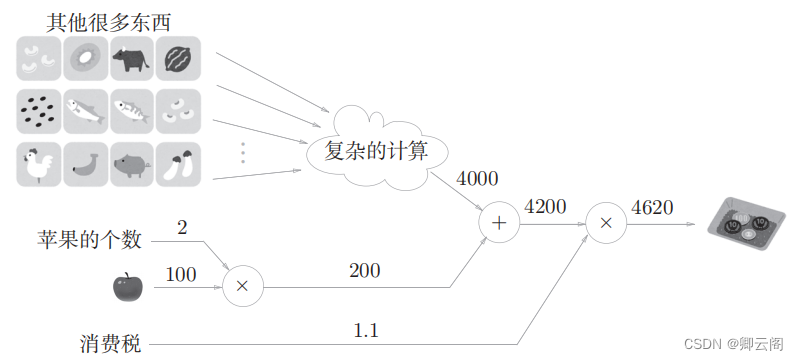
我们用一个具体的例子来说明局部计算。比如,在超市买了2个苹果和其他很多东西。时,可以画出如图5-4所示的计算图。
假设总共花费4000日元。这里的重点是,各个节点处的计算都是局部计算。这意味着,例 如苹果和其他很多东西的求和运算(4000 + 200 → 4200)并不关心4000这个 数字是如何计算而来的,只要把两个数字相加就可以了。换言之,各个节点处只需进行与自己有关的计算(在这个例子中是对输入的两个数字进行加法 运算),不用考虑全局。
5.1.3 为何用计算图解题
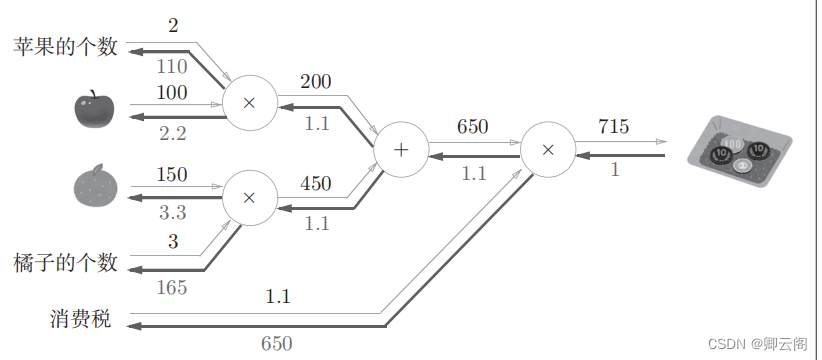
使用计算图最大的原因是,可以通过反向传播高效计算导数。在介绍计算图的反向传播时,我们再来思考一下问题 1 。问题 1 中,我们计算了购买2 个苹果时加上消费税最终需要支付的金额。这里,假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额,即求“支付金额关于苹果的价格的导数”。设苹果的价格为x ,支付金额为 L ,这个导数的值表示当苹果的价格稍微上涨时,支付金额会增加多少。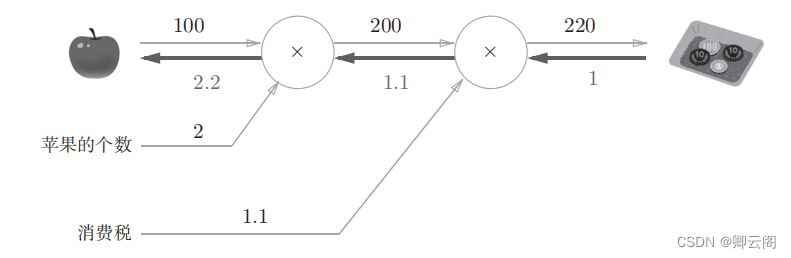
反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1 → 1.1 → 2.2)。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1日元, 最终的支付金额会增加2.2日元(严格地讲,如果苹果的价格增加某个微小值, 则最终的支付金额将增加那个微小值的2.2倍)。
这里只求了关于苹果的价格的导数,不过“支付金额关于消费税的导数”“支付金额关于苹果的个数的导数”等也都可以用同样的方式算出来。并且,计算中途求得的导数的结果(中间传递的导数)可以被共享,从而可以高效地计算多个导数。综上,计算图的优点是,可以通过正向传播和反向传播高效地计算各个变量的导数值。
5.2 链式法则
5.2.1 计算图的反向传播使用计算图的反向传播的例子。假设存在 y = f ( x ) 的计算。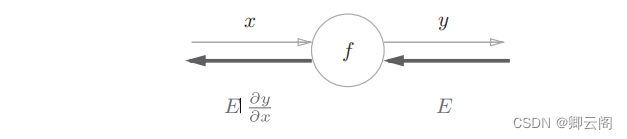
5.2.2 什么是链式法则
介绍链式法则时,我们需要先从 复合函数 说起。复合函数是由多个函数构成的函数。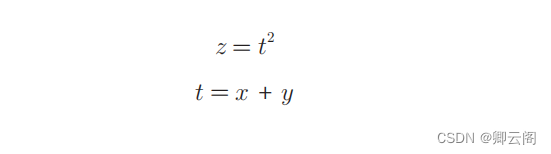 这就是链式法则的原理,乍一看可能比较难理解,但实际上它是一个非常简单的性质。
这就是链式法则的原理,乍一看可能比较难理解,但实际上它是一个非常简单的性质。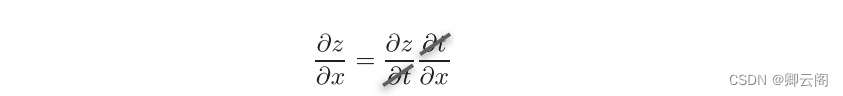
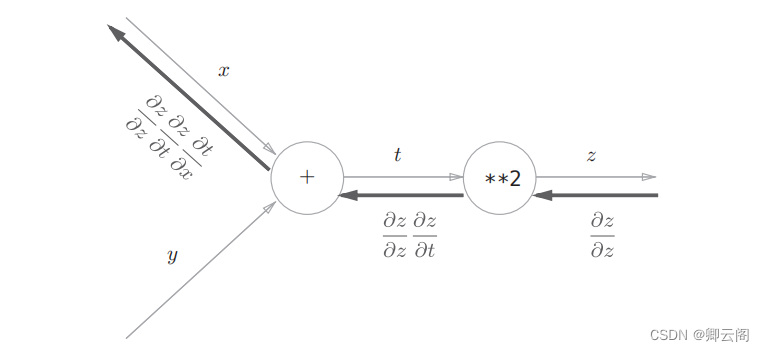
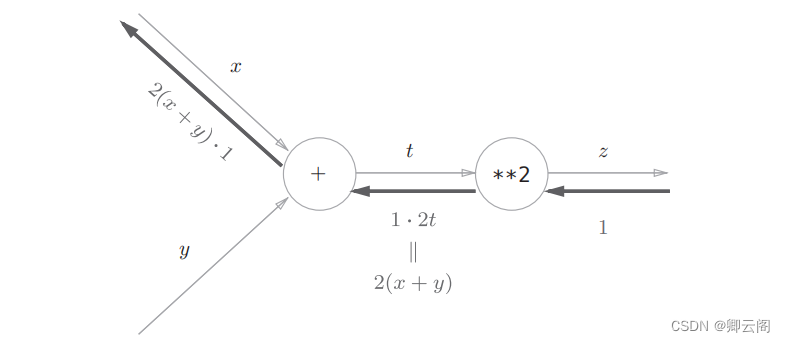
5.2.3 链式法则和计算图
5.3 反向传播
5.3.1 加法节点的反向传播
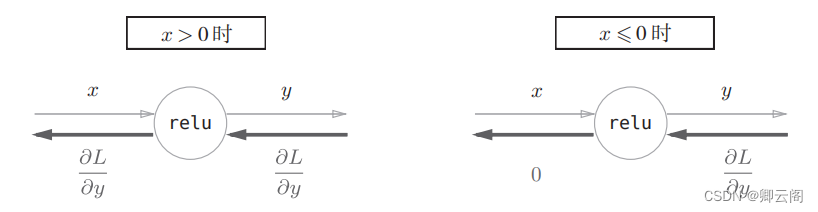
5.5 激活函数层的实现
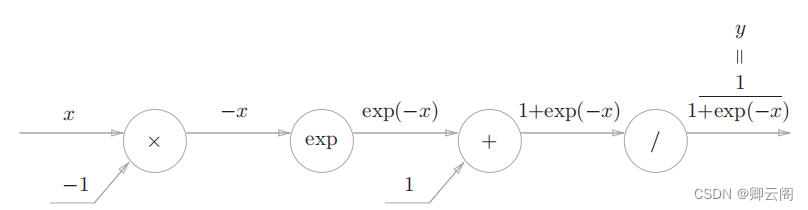
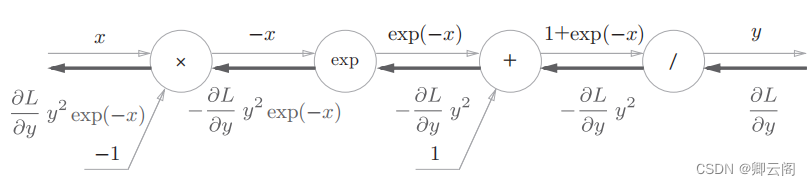
5.5.2 Sigmoid层
5.6 Affine/Softmax层的实现
5.7 误差反向传播法的实现
5.7.1 神经网络学习的全貌图
前提神经网络中有合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为学习。神经网络的学习分为下面 4 个步骤。步骤1(mini-batch)从训练数据中随机选择一部分数据。步骤2(计算梯度)计算损失函数关于各个权重参数的梯度。步骤3(更新参数)将权重参数沿梯度方向进行微小的更新。步骤4(重复)重复步骤 1 、步骤 2 、步骤 3 。
0基础入门---第四章---误差反向传播法
news2026/2/12 21:39:43
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/693901.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Java性能权威指南-总结19
Java性能权威指南-总结19 Java EE性能调优JVM线程调优调节线程栈大小偏向锁自旋锁线程优先级 小结 Java EE性能调优Web容器的基本性能 Java EE性能调优
JVM线程调优
JVM的某些调优策略可以影响线程和同步的性能。
调节线程栈大小
当空间非常珍贵时,可以调节线程…
Day6——Web安全基础
网络安全学习笔记Day6 Web安全基础 一.Web简介什么是Web?什么是因特网?互联网,因特网,万维网的关系万维网构想的诞生http协议URL 二.Web发展史Web1.0Web2.01.0与2.0的区别Web1.0的安全漏洞Web2.0的安全漏洞 三.杂项门户网站静态页…
戴尔笔记本如何用U盘重装Win10系统?
戴尔笔记本如何用U盘重装Win10系统?很多使用戴尔笔记本的用户,都想知道如何用U盘来重装Win10系统,用户首先要确认自己的戴尔笔记本电脑能不能联网,然后再准备一个8G以上的U盘,最后根据小编分享的戴尔笔记本用U盘重装Wi…
Springboot Mybatis 不存在插入数据,存在则更新数据
前言 是不是经常看到代码, 查一下数据库,如果存在数据,就做更新语句调用; 如果不存在,就插入。 今天该篇介绍的 是使用 INSERT INTO ON DUPLICATE KEY UPDATE 来实现我们上述的场景, 不需要…
不能真“生成代码”的“低代码”平台,不可能获得程序员的认可
目录
前言
思考
解决问题
基本现状
发现亮点 前言
>前几天我和一个好友聊天的时候,他是这么评价低代码平台的:“想证明程序员都是傻X,又想让程序员买单!程序员本身心里就不爽... ” 那么,低代码发展势头迅猛的…
Live800:客服系统如何帮助企业优化服务流程
随着互联网的发展和社会进步,客服服务已经成为企业经营中不可或缺的一部分,然而,客服服务一直以来都备受诟病,用户对客服人员的不满情绪也随之而来。显然企业急需提升客户服务质量,这就离不开客服系统的帮助。 那么&am…
Linux系统中的信号
信号是由用户、系统或者进程发送给目标进程的信息,以通知目标进程某个状态的改变或系统异常。Linux信号可由如下条件产生:
对于前台进程,用户可以通过输入特殊的终端字符来给它发送信号。比如输入CtrlC通常会给进程发送一个中断信号…
Maven项目,本地jar包导入手动导入到Maven库中
当你的项目,由于网络或者环境这些问题,无法从maven中央仓库更新jar包到本地的时候,可以尝试下面方法,手动添加jar包到Maven仓库;
方法一(推荐):
1、需要先拿到你的jar包࿰…
Linux——3Linux用户和权限
目录
3.1 认识root用户
root用户(超级管理员)
su 和 exit命令
sudo命令
3.2 用户、用户组
3.3 修改权限控制 - chmod
3.4 修改权限控制 - chown
3.1 认识root用户
root用户(超级管理员) 无论是Windows、MacOS、Linux均采…
8.10 TCP是如何实现可靠传输的
目录
TCP 最主要的特点
面向流的概念
Socket 有多种不同的意思
TCP是如何实现可靠传输的?
A 如何知道 B 是否正确收到了 M1 呢? 确认丢失
确认迟到 连续 ARQ 协议
累计确认
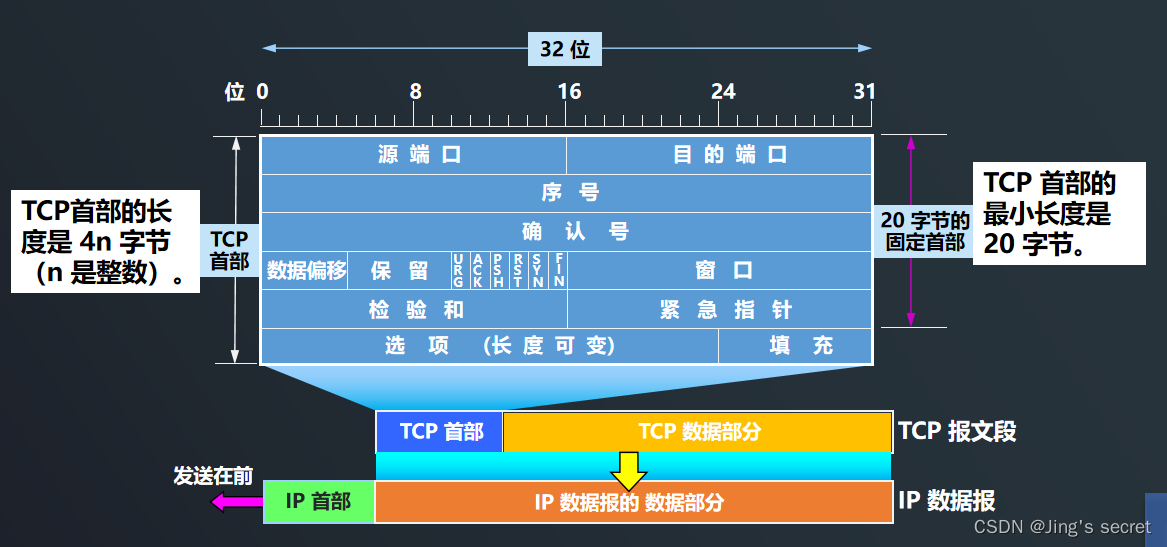
TCP报文段的首部格式 TCP 最主要的特点
TCP 是面向连接的运输层协议&a…
基于Java理发店会员管理系统设计实现(源码+lw+部署文档+讲解等)
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…
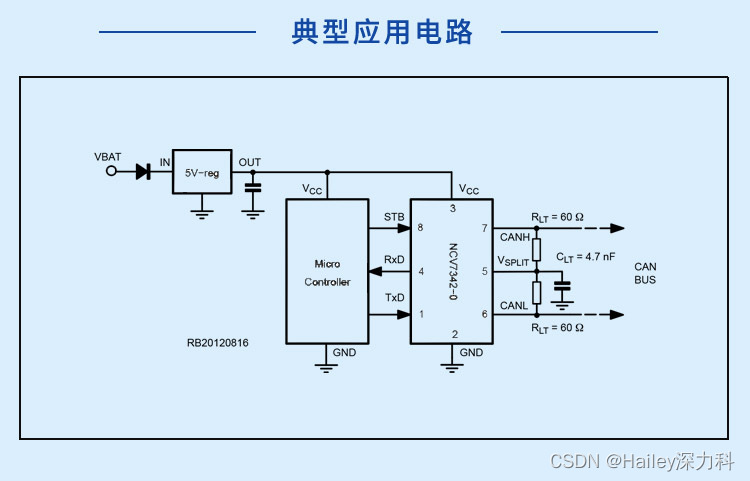
深入探析CAN收发器NCV7342D10R2G各项参数
NCV7342D10R2G安森美深力科 CAN收发器是控制器局域网(CAN)协议控制器和物理总线之间的接口,可用于12V和24V系统。收发器向总线提供差分传输能力,向CAN控制器提供差分接收能力。由于接收器输入的共模电压范围很宽能够达到卓越的电磁…
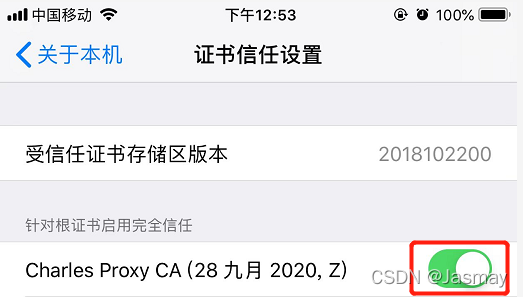
charles unknown 问题和手机代理设置(iOS手机)
一、Charles下载 下载地址:https://www.charlesproxy.com/download/ 二、Charles配置代理 1.查看本机IP:help-->Local IP Address
2.查看或者设置访问端口:Proxy->Proxy Settings 3.设置不代理计算机的请求(推荐࿰…
【Java】Java核心 76:XML解析 Dom4j (下)
文章目录 **3** **使用xpath技术结合DOM4J技术读取xml文件(了解)**1.概念介绍2.XPath使用步骤3.XPath语法(了解)3.1全文搜索路径表达式方式 掌握 3 使用xpath技术结合DOM4J技术读取xml文件(了解)
1.概念介绍
问题:通过上面的案例我们发现有个小问题.就是获取标签的…
Python程序设计期末作品完整版|代码和程序设计文档
python程序设计作品,希望对您有帮助,希望您的一键三连! 程序设计报告
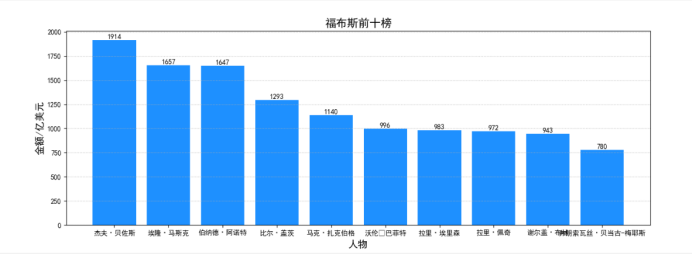
1.爬取数据的意义 富豪榜的出现,体现了人们思想的变化:由保守藏富向正向面对财富的转变;由保守向文明开放(–说明了大众媒体的进步与教育的普及等思想工具的极…
会网络爬虫能干什么?
网络爬虫是一种自动化程序,用于浏览互联网并从网页中获取数据。它可以执行以下任务:
数据采集:网络爬虫可以访问网站,并从中提取所需的数据,例如新闻文章、产品信息、用户评论等。这些数据可以用于各种目的࿰…
【数据结构导论】第 2 章:线性表
目录
一、线性表的基本概念
(1)线性表的基本概念
(2)线性表的逻辑结构特征
(3)线性表的基本运算
二、线性表的顺序存储
(1)线性表顺序存储的类型定义
(2&…
PHP 旅游网站系统mysql数据库web结构apache计算机软件工程网页wamp
一、源码特点 PHP 旅游网站系统 是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为PHP APACHE,数据库为 mysql5.0,使用php语言开发。
代码…
Spark15-16
15. SparkOnYarn
15.1 Hadoop YARN回顾
15.1.1 YARN 的基本设计思想
将Hadoop 1.0中JobTracker拆分成两个独立的服务,一个全局的资源管理器ResourceManager(RM)和每个应用独有的ApplicationMaster(AM).其中RM负责整个系统的资源管理和分配,而AM负责单个的应用程序的管理 15.…