【江西省研究生数学建模竞赛】题目之一蒸汽发生器倒U型管内液体流动

在这里插入图片描述

1 题目

2023年江西省研究生数学建模竞赛题目之一

荧汽发生器倒U型管内液体流动

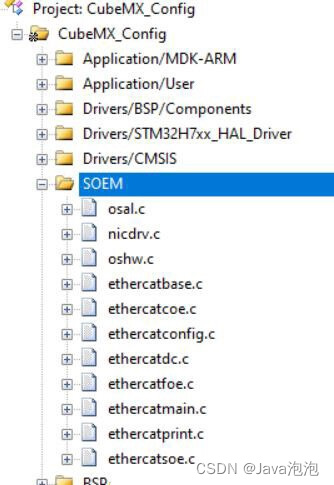
PACTEL压水堆整体测试设备在2009年建造，用于带有垂直倒U型管莱汽发生器的压水堆热液压相关的安全性研究，参见图1。

在这里插入图片描述

图 1：蒸汽发生器示意图（左）和PACTEL压水堆总体视图（右）

PACTEL压水堆设施包括一个反应堆压力容器模型、两个带有蒸汽发生器的回路、一个连接到一个回路的稳压器和应急堆芯冷却系统。压力容器为U型管结构，代表降液管、下增压室、芯体和上和气室。PACTEL压水堆设备内的蒸汽发生器U型管束包含51根倒U型管，排成10行。表1列出了每一行的U型管的管数N、高度H、管长l和弯管半径r。U 型管的内径和外径分别为D = 16.57mm和 $D_i$ = 19.05mm。

通过自然循环，冷却剂从每根倒U型管道的一侧流动到另一侧，把核反应装置中的非能动余热排出，从而提升反应堆固有安全性能。蒜汽发生器倒U型管内可能存在负的进出口压降，从而诱发冷却剂倒流现象，导致系统内部的冷却剂流量低于设计值，严重影响一回路冷却剂系统的热量输运，给反应推的运行安全带来极大挑战。对倒U型管倒流现象进行分析，研究蒸汽发生器并联倒U型管间的流量分配特性，评估自然循环条件下蒸汽发生器的流动不稳定性，对反应堆的运行安全性能具有重要意义。

在这里插入图片描述

把倒U型管流入一侧称为一次侧，流出一侧称为二次侧。当管道内流量非常小时，二次侧可能发生倒流现象。由于U型管道为细长形，相关物理量仅和管线 $\leq s \leq l)$ 方向有关。为了进一步简化，假设U型管内流体速度v量定。

问题1，对一根U型管中的液体流动建立模型，研究液体的温度T、密度 $\rho$ 对管线s的依赖。

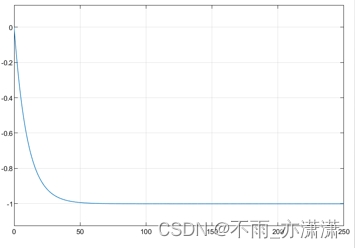
问题2; 研究一根U型管的进出口压差 $\Delta p$ 如何依赖管内流体速度w，进而分析形成液体倒流的原因。请画出 $\Delta p$ 和v之问关系的一条曲线。当 $\Delta p$ 大于某个临界值（最小压差），管内液体向前流动，称之为正流管; 否则，管内液体倒流，称之为倒流管。根据表1中的数据，计算每种类型的U型备，计算最小压关，并填入表1中的最后一列中。

问题3，以PWR PACTRT 模型下的蒸汽发生器为计算对象。10 组倒U 型管的管长依次增加（见表1) ，第i组倒U型管数基为 $N_i$ 根。在进行并联倒U型管流最分配计算时，假设并联倒U型管进出口压力相同，所有正流管进口温度相同。蒸汽发生器内部的进出口压降和系统压力相比非常小，实际中难以测量，所以将进出口压降视为未知量。系统内自然循环的流量低，很难准确测出流量的准确值，因此将一次侧进口流量也视为未知量。蒸汽发生器是一二次侧热量交换的场所，忽略一次侧通道中热基在沿程传递时的损失，单位时间内通过倒U型管传递到二次侧的热量约等于反应堆在单位时间内发出的热量，即反应堆功率P。

（1）请给出算法计算给定反应推功率下每个管道的流动情况。

（2）通过表1中的数据，计算分析U型管内倒流管占的比例，并研究这些倒流管和它的管长之间的关系。

（3）分析哪些途径可以减少倒流现象。

问题4; 请对U型管中的液体流动模型进行改进，重新探讨上述3个问题。

2 建模思路

2.1 问题一

要建立液体流动模型可以采用连续性方程和动量守恒方程。其中连续性方程描述了流体流动的质量守恒，动量守恒方程描述了流体流动的动量守恒。通过这两个方程可以计算出流体的速度、温度和密度等基本参数。

2.2 问题二

（1）画 $\Delta p$ 与流体速度v之间的关系简化模型

由于管道中流量非常小时，可以假设U型管内的流体速度v量定。考虑U型管水平放置时的液体高度 $h$ 、液体密度 $\rho$ 和加速度 $g$ ，并根据质量守恒定理和伯努利方程求解出液体在管道内的流动速度 $v$ 。

（2）分析液体倒流的原因

要通过建立简化的液体动力学模型，分析U型管的进出口压差和流体速度之问的关系，描绘出这种关系的曲线，并结合液体动力学原理，分析液体倒流的原因。

当进出口压差小于某个临界值（最小压差）时，管内液体倒流。这个最小压差具体是多少，需要先计算出来，然后填入表1中最后一列。对于倒流管和正流管，这个最小压差是不同的。液体倒流的原因要从液体动力学入手。一般而言，当管道中液体的流速下降到低于某个特定阈值时，由于粘滞力等因素的影响，容易使得倒弯处的管壁出现液体附着现象，从而出现回流现象。对于倒U型管，这种回流现象会导致液体从二次侧流入一次侧。因此，要减少液体倒流，可以从两方面入手：一是增加管子弯曲的半径，二是增加液体的流速。对于这两方面，可以优化倒U型管的设计，增加其防倒流的能力。不同的设计方案可能会对液体的流动速度、阻力、压降、热传递等产生影响，要综合考虑各种因素。

2.3 问题三

（1）计算给定反应推功率下每个管道的流动情况。

考虑使用数值模拟的方法计算每个管道的流动情况，可以采用计算流体力学（CFD）方法。具体步骤如下：

1.构建几何体模型：将蒸汽发生器的几何体进行建模，包括倒U型管（长、高、宽、内径等），管道（长度、宽度等）和进出口（口径、位置等）等内容。

2.经验公式的输入：将表1中的管道数据和反应堆功率P输入数值模拟软件。

3.边界条件讨论：确定每个物理量的边界条件，包括进出口流量、进口温度、压降等等。

4.模型求解：使用CFD方法对蒸汽发生器进行求解，得到每个管道内部的流速、流量和压力等物理量。

5.分析结果：根据结果分析每个管道的流动情况和是否满足设计要求，如果不满足设计要求，可以对模型进行修改，并重新进行数值模拟。

（2）计算分析U型管内倒流管占的比例，并研究这些倒流管和它的管长之间的关系

第一步：计算U型管内倒流管所占的比例：

通过进行数值模拟，计算出每个倒U型管内部的液体流动情况。根据流量、压力等物理量的分布情况，对流动方向进行分析，统计出每个倒U型管内倒流管的数量，并计算出倒流管所占的比例。

第二步：研究倒流管和管长之间的关系：

对于每个倒U型管，根据表1中的数据，分别计算出管长 $L_i$ 和倒流管数量 $N_{back,i}$ ，并将数据进行可视化处理，得到管长和倒流管数量之间的趋势关系图。同时，还可以对管长和其他物理量（如压力、流量等）之间的关系进行分析，找出相关性并进行进一步探讨。

（3）以下是我想到的角度减少倒流现象，不限于以下方法：

1.加强管道支撑和固定。管道失稳是导致倒流现象的主要原因之一，所以加强管道的支撑和固定可以有效减少管道的振动和摆动，从而减少倒流发生的概率。

2 改进蒸汽发生器的设计。可以通过改变U型管的形状和大小等参数来改进蒸汽发生器的设计，减少倒流现象的发生。例如，可以适当增加U型管的内径和外径，降低管道的摩擦阻力，从而减小压降，降低倒流风险。

3.优化冷却剂流动。在设计冷却剂流动系统时，可以采用合理的流动分布方式，使得所有倒U型管道中的流量分配均匀，从而避免流量局部过大或过小所导致的倒流现象。

4.增加稳压器的调节精度。通过增加稳压器的调节精度，能够减少二次侧的压力震荡和波动，降低倒流的概率。

5.加强检测与监控。可以采用现代化的检测和监控技术，对压力、温度、流量等参数进行实时监测，及时发现并处理倒流现象，保障反应堆的安全运行。

2.4 问题四

从改进蒸汽发生器的设计的角度去探讨。改进的其中一个方法是调整倒U型管的形状和大小等参数，进而减少管道内的压降，从而降低倒流现象的风险。具体来说，可以通过增加U型管的内径和外径来改进设计，进而降低管道的摩擦阻力，减小压降。同时，也可以通过调整管道的弯曲半径等参数来改善管道的流动状态，进一步降低压降。

3 建模方案

模型假设

（1）内部液体速度是均匀的

（2）液体的比热容和流量均为常数

（3）管内阻力主要由摩擦力和弯曲阻力组成

（4）极小化管内进出口压差为目标

3.1 问题一

用连续性方程和动量守恒方程建立U形管液体流动模型。由于流体速度为常数，方程可以简化，连续性方程为：

$\nabla \cdot (\rho v) = 0$

动量守恒方程为：

$\nabla p = \rho g + F$

由流体力学理论可知，当液体处于静态平衡时，液面高度 $h$ 与U型管线s的关系为：

$\frac{dh}{ds} = -\frac{\rho g}{\nabla p}$

由热力学理论可知，压力 $p$ 、温度 $T$ 和密度 $\rho$ 之间的关系为：

$\rho RT$

$。。。略，请下载完整文档$

3.2 问题二

（1）画 $\Delta p$ 与流体速度v之间的关系简化模型

假设第 $i$ 个U型管中，一次侧的液体高度为 $h_i$ ，则一次侧流入流量为 $Q=m_i/A_i$ ，流出流量为 $Q'=(m_i+\Delta m_i)/A_i$ ，其中 $\Delta m_i$ 表示单位时间内的液体质量，且可以得到：

$\begin{cases}h_i+\frac{\Delta m_i}{\rho A_i}=h_i\\h_i+\frac{m_i}{\rho A_i}=h_0\end{cases}$

即 $\Delta m_i=-\rho Q'_i(v_i)\Delta s_i$ ，其中 $Q'_i(v_i)$ 表示在速度为 $v_i$ 时的单位时间内流入的流量。

同时假设倒U型管中的液体速度均匀，然后利用伯努利方程综合以上假设得：

$\Delta p_i=\rho\cdot g\cdot(h_0-h_i)-2\cdot\rho\cdot v_i^2\cdot k_i$

$。。。略，请下载完整文档$

（2）分析液体倒流的原因

基于以上假设，建立数学模型来分析原因，需要通过数值模拟或其他方式优化目标函数 $F$ ，找到使得 $F$ 最小的 ${w_i\}$ ，具体模型如下。

质量守恒定律：

$Q'_i=\pi\cdot r_i^2\cdot w_i=N_i\cdot Q\pm m_i\cdot\frac{\partial w_i}{\partial x}$

倒U型管内的液体流动速度 $v_i$ ：

$v_i = \frac{Q_i}{\pi\cdot r_i^2}$

倒U型管内的电阻：

$R_i=R_{f,i}+R_{b,i}=\frac{16\mu_i\cdot l_i}{\pi\cdot D_i^4}+\frac{\rho_i\cdot A_i^2}{2\cdot k_i\cdot r_i}$

其中， $R_{f,i}$ 为摩擦电阻， $R_{b,i}$ 为弯曲电阻， $\mu_i$ 为点密度； $l_i$ 、 $D_i$ 、 $\rho_i$ 、 $A_i$ 和 $k_i$ 分别为倒U型管的长度、直径、密度、横截面积和弯曲半径。

进出口压差 $\Delta p_i$ ：

$\Delta p_i = \rho_i\cdot g\cdot H_i + R_i\cdot v_i$

$。。。略，请下载完整文档$

3 问题三

（1）计算给定反应推功率下每个管道的流动情况。

根据思路的步骤，建立的数学模型可以表示为：

第一步：几何体模型建立：
$V_{i}=l_{i}\cdot\pi\cdot r_{i}^2, \quad V_{j}=l_{j}\cdot w_{j}\cdot h_{j}$

其中， $V_{i}$ 表示倒U型管的体积， $V_{j}$ 表示管道的体积， $l_{i}$ 、 $r_{i}$ 、 $l_{j}$ 、 $w_{j}$ 和 $h_{j}$ 分别为倒U型管的长度、半径和管道的长度、宽度和高度。

第二步：经验公式的输入：
$\Delta p_{i}=16\mu_{i}\frac{L_{i}}{\pi r_{i}^4}Q_{i} + \frac{\rho_{i}L_{i}}{\pi r_{i}^2}\frac{Q_{i}^2}{2\pi^2 r_{i}^2} + \frac{C_{i}^2}{2g}$

其中， $\Delta p_{i}$ 表示倒U型管 $i$ 中液体通过所需的压降， $\mu_{i}$ 、 $\rho_{i}$ 、 $L_{i}$ 和 $r_{i}$ 分别表示介质的动力粘度、密度、长度和半径， $Q_{i}$ 为管内液体的流量， $C_{i}$ 为液体通过管道 $i$ 中时的流速。