KY:datasets, neural networks, gaze detection, text tagging
AB:RSs通常建立在大型(可能是非常稀疏的)数据集上,因此妨碍了非常复杂去偏技术的使用。我们的方法引入了一个公平函数(fairness functional),它最小化了组间的损失差异,并避免了后处理步骤。这使我们能够适应大多数推荐系统基础的算法,如FM及其许多泛化和去偏差。我们给出了这样一个函数的例子,并表明它的属性是理想的适合于多利益相关者公平RS的情况。最后,我们证明了我们的方法在基准数据集上的实践效果很好,并且部分去偏是必不可少的,因为完全去偏可能会导致较差的泛化。
文章目录
- 1 intro
- 2 公平推荐系统
- 2.1 RS模型
- 2.2 RS公平
- 2.3 方法举例
- 3 fairness functional方法
- 3.1理解现有的公平性技术
- 3.2 group functionals
- 3.3 例子
- 3.4 最优化
- 3.5 组functions中的公平性
- 3.6加权对数和指数法
- 4 多方公平
- 4.1 交叉性和丰富的子群公平性
- 4.2 维度诅咒
- 5 实验
- 5.1 Historically Disadvantaged Groups
- 5.2 评级分类
- 5.3 排名
- 6 讨论
1 intro
本文的主要目标是为推荐系统中的偏差缓解提供一个灵活的框架。我们将这样一个框架的要求正式化:
(1)缓解偏差的方法应简单直接,透明且易于解释;(2)去偏应可调,以保持权衡可控制;(3)提出的算法应是可训练的,以避免后处理步骤和在生产中使保护特征;(4)该方法应能够包含RS文献中确定的大部分偏差;(5)可伸缩性和适应现有许多的推荐系统。
我们的主要贡献是引入了fairness functional的概念,旨在共同完成两个不同的任务,即损失最小化和 disparity最小化。我们首先在用户公平性的情况下描述这个框架,然后将其扩展到多利益相关者的情况。
2 公平推荐系统
2.1 RS模型
(略,这部罗列了模型名称和对应文献)
2.2 RS公平
(略,这部罗列了各种bias及其主观分类)
我们主要关注popularity bias和activity bias,以及unfairness,但所提出的框架足够灵活,可以处理其他类型的bias。
2.3 方法举例
用户N个,项目M个,用户组G^ U有A个,项目组G^I有B个。这些组可以通过上下文信息(如用户和/或项目的某些特征)来定义,也可以通过内源性信息(例如,通过活动水平和受欢迎程度)来定义.我们考虑两个典型的推荐系统的例子,
1)评级分类,其主要目标是预测用户显式反馈;

2)个人的排名列表,隐式反馈是高度相关的(交互反映用户的项目偏好)。大多数RSs都是这两种方法的(混合)变体。

3 fairness functional方法
在本节中,我们的观点是将RS目标损失分解为组级期望损失函数,最后将此构造推广到更广泛的函数类。类似的方法也应用于[6]中的无监督学习。
3.1理解现有的公平性技术
大多数针对位置、选择、曝光、流行和活动偏差的去偏技术可以通过引入置信权重Wu、i和一个(通常)更复杂的损失函数ℓ˜来总结,这样要最小化的总体损失被写成:请注意,通过设置W_u,i = 1和ℓ˜=ℓ,可以恢复原始(有偏差的)设置。

假设项目和用户是按A组进行分类的(如U×I=∪_a=1^A g_a), 活跃/不活跃用户:根据受保护的特征分组;流行/不流行项目:根据r_u,i=a分组;重写损失函数:

这是我们现在介绍的群函数的最直接的例子。
3.2 group functionals
这导致我们通过修改损失函数和引入不同的映射(而不是线性映射)来得到公平RS的定义:
定义1——假设映射T :R A → R在其每个参数中都是一个非递减函数,那么我们将关于T的公平广义推荐系统定义为最小化以下目标函数

这个定义适用于所有的functionals T,但我们自然会关注那些旨在减少组间差异的functionals T。注意,通过建立一个类似的映射R(d×a)→R,它可以很容易地推广到vector-valued平均损失函数。此外,群函数的和与组合在本质上仍然是群函数。
3.3 例子
让我们在这里介绍一些众所周知的公平functionals,主要来自于监督学习文献。
标准和重加权损失函数、Minmax、Lp范数、Penalised/Regularised学习、对抗技术(详见原文)。
【公平函数?这里例举的就是常见的公平推荐方法阿…】
3.4 最优化
概括:公平性作为在梯度下降期间的“权重适配器”的功能。
3.5 组functions中的公平性
我们将公平性理解为减少群体间的成本差异(即平均损失的差异),简而言之,确保所有群体分担“统计负担”;因此,RS所犯的错误在组之间应该有相同的平均值。损失函数ℓ,它惩罚估计误差和偏离实现值,例如,评级错误分类。可以推广到其他公平定义如机会均等(通过考虑多个泛函和损失函数)。
3.6加权对数和指数法
在本节中,我们将重点关注一个特定的群函数,即加权对数和指数法(或“wLSE”)。对数和指数(“LSE”)在机器学习中被广泛使用,但我们在这里引入了一个轻微的修改,允许一个额外的加权方案:
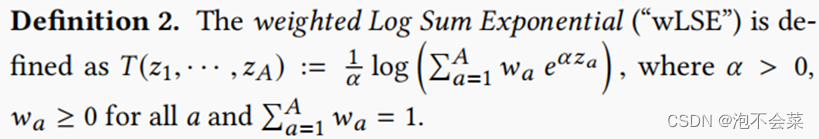
【往后没看懂,略,后边实验用到了wLSE】
4 多方公平
根据组的笛卡尔积来定义一个新的分割(或用户和项的划分),从而导致交叉性。而公平functions的定义适用于用户/项目空间的任何划分,值得讨论交叉性和多利益相关者公平性的挑战。
4.1 交叉性和丰富的子群公平性
偏差可以在交叉水平上明显,但不能在边际水平上明显(即,公平仅针对一种利益相关者进行衡量)
4.2 维度诅咒
交叉性的一个缺点是实际组的数量以A×B增长,这可能是禁止的。另一个问题通常是群体失衡。例如,如果a组和b组分别代表活动加权用户和项目总数的5%,那么交叉组占总数的0.25%。因此,可能很难在输出中获得足够的鲁棒性和保证泛化。
另一种方法是同时最小化用户和项目之间的边际差异。这些损失之间的依赖性是有保证的,由于共享模型参数θ和每个损失ℓ,这个概念通过以下定义得到严格的:、
Def3:多个利益相关者的边际公平函数被定义为一个映射T: R^A+B→R,它在其每个参数中都是一个非递减函数,这样公平广义推荐系统就可以使以下目标函数最小化
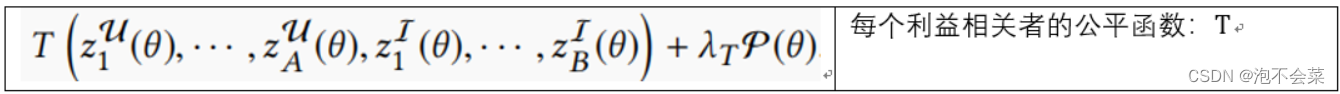
5 实验
公平通常是非常特定于领域和上下文的。我们提出的基于公平泛函的RS框架,虽然广泛适用,但并没有逃避上下文化的需要。此外,具有不同类型偏差(外源性和内源性)的RS数据集很少公开。为了克服这一障碍,我们首先将我们的方法应用于具有外生属性的非RS数据集,然后在“传统的”RS数据集上说明它,并应用于评级分类和个性化排序。
5.1 Historically Disadvantaged Groups
数据集:Adult;保护属性:种族
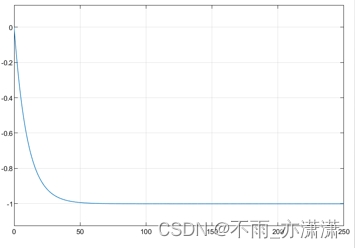
使用不同的超参数值函数训练一个简单的正则化单层神经网络,wLSE函数具有不同的超参数值α。图2显示了增加α会导致公平性的增加,并说明了统计性能和公平性之间的权衡[2,26]。α = 0对应于非去偏的情况,而α=+∞是最小-最大设置[16,37]。在其他公平泛函和其他数据集上也得到了类似的结果。然而,为了简洁起见,读者可以参考[2,27]以获得进一步的结果和基准测试。
5.2 评级分类
本实验的目的是为了展示公平函数方法的广泛适用性。因此,我们将其应用于多个现有的最先进的RS算法,并表明,结果定性地指向样本外差异的减少。
数据集:Amazon的三个,ML1M、前5%为优势群体,后95%为若是群体,
模型:18种,是为了说明,公平性函数是一种元算法,它与特定的底层RS无关。
然后围绕Increasing Fairness、丰富的子组的公平性或交叉性、超参数选择的影响、权衡展开。
5.3 排名
数据集:Amazon的一个、Yelp
Metric:【B34】相对标准差of统计均等(RSP)和机会均等(REO)。
然后围绕算法和实施、参数选择、提升公平、Benchmarking 和 SOTA展开。
6 讨论
在本文中,我们引入了公平泛函(公平functionals)的概念,并将其应用于群体平均损失,从而减少了群体间的成本差异。设计公平的RSs已经导致了一个通用框架,适用于所有已知的RS算法。我们的方法的一个显著优点是它的简单性。
由于它的普遍性,我们还指定了一个特殊的公平函数的选择,即加权对数和指数,这是非常实用的,并受益于许多有趣的理论性质。总之,用户只需要选择一个超参数α来控制所需的公平-准确性权衡。重要的是,部分去偏通常是比最小-最大方法(对应于设置α=+∞)更好的选择,正如我们的一些样本外结果所强调的那样。