518. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。 

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]

输出：4

解释：有四种方式可以凑成总金额： 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]

输出：0

解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10]

输出：1

动归五部曲：

1. dp数组和下标的含义

dp[i]：凑成总金额j的货币组合数为dp[i]

2. 确定递推公式

dp[j] += dp[j - coins[i]]

3. dp如何初始化

dp[0] = 1

4. 确定遍历顺序

外层遍历金钱总额，内层遍历钱币

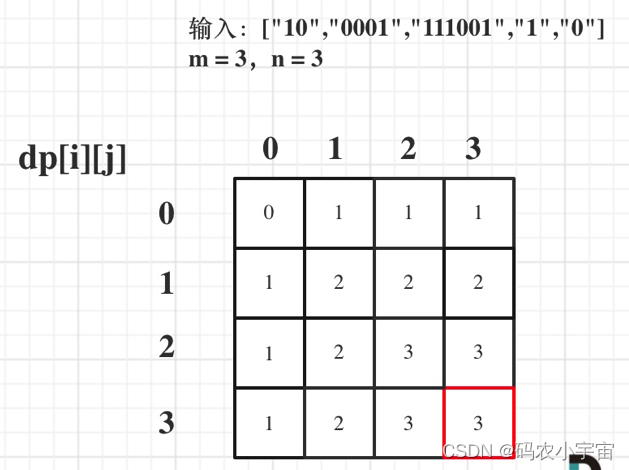
5. 举例推导dp数组

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for(int i = 0;i < coins.length;i ++){
            for(int j = coins[i];j <= amount;j ++){
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

377. 组合总和 Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4

输出：7

解释： 所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3

输出：0 

 动归五部曲:

1. dp数组和下标的含义

dp[j]表示和为j的组合的个数

2. 递推公式

dp[i] += dp[j - nums[i]]

3. dp数组如何初始化

dp[0] = 1

4. 遍历顺序

target外循环，nums内循环

5. 举例推导dp数组

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for(int i = 0;i <= target;i ++){
            for(int j = 0;j < nums.length;j ++){
                if(i >= nums[j]){
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}