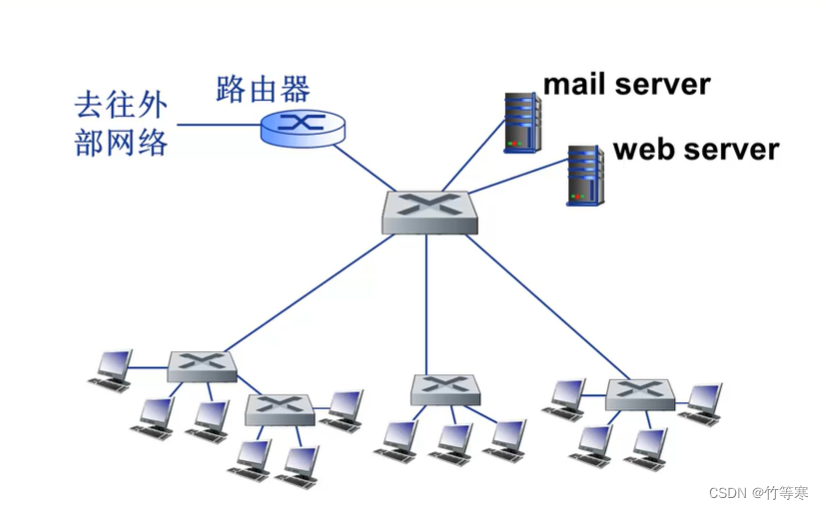
基于OpenCV的傅里叶变换

傅里叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在图像中变化剧烈的地方（比如边界）经过傅里叶别换后就相当与高频，反之变化缓慢的地方就是低频。傅里叶变换可以将图像变换为频率域， 傅立叶反变换将频率域变换为空间域。

1. 图像处理中的傅里叶变换

傅里叶变换是一种有用的图像处理方法，可将图像分解为正弦和余弦分量。

傅里叶频域的图像由傅里叶变换的输出表示，而空间域的等效图像则由输入图像表示。傅里叶频域图像中的每个点表示空间域图像中包含的一个频率。

图像分析、图像滤波、图像重建和图像压缩都是使用傅里叶变换的应用。

2. 傅里叶变换的作用

高频：变化剧烈的灰度分量，例如边界

低频：变化缓慢的灰度分量，例如一片大海

低通滤波器：只保留低频，会使得图像模糊

高通滤波器：只保留高频，会使得图像细节增强

OpenCV中主要就是傅里叶变换cv2.dft()和逆傅里叶变换cv2.idft()，输入图像需要先转换成np.float32 格式。得到的结果中频率为0的部分会在左上角，为了方便分析通常要转换到中心位置，通过dst=numpy.fft.fftshift(src)函数处理后，图像频谱中的零频率分量会被移到频域图像的中心位置。cv2.dft()返回的结果是双通道的（实部，虚部），通常还需要转换成图像格式才能展示（0,255）。

2.1 理论基础

如何使用 OpenCV 应用傅立叶变换。

傅里叶变换将图片分成正弦和余弦分量。换句话说，它将图像的空间域变为频域。即任何函数都可以通过添加无限正弦和余弦函数来精确逼近。二维图像的傅里叶变换在数学上定义为：

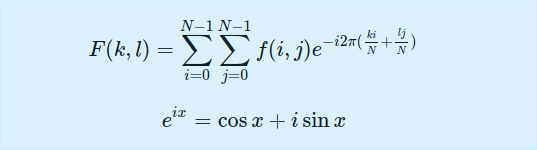
空间域的图像值为f，频域的图像值为F。复数是变换的结果。这可以以两种方式显示：作为真实图像和复数图像，或作为幅度和相位图像。然而，在整个图像处理方法中，只有幅度图像是有用的，因为它提供了我们需要的关于图像几何结构的所有信息。但是，如果您想对这些形式的图像进行更改然后重新转换它，则需要保留它们。

2.2 python代码实现

import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('D:/cat2.jpg',0) #0表示灰度图
img_float32 = np.float32(img)#转换格式
#傅里叶变化
dft = cv2.dft(img_float32, flags = cv2.DFT_COMPLEX_OUTPUT)
#将图像频谱中的零频率分量会被移到频域图像的中心位置
dft_shift = np.fft.fftshift(dft)
#得到灰度图能表示的形式
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

2.3 C++ 代码实现

#include <opencv2/highgui.hpp>
#include <opencv2/imgcodecs.hpp>
#include <opencv2/imgproc.hpp>
#include <iostream>


void showImg(cv::Mat&, const std::string& );

void expand_img_to_optimal(cv::Mat& , cv::Mat& );
cv::Mat fourier_transform(cv::Mat& );
void crop_and_rearrange(cv::Mat& );



int main(int argc,char** argv)
{
	cv::Mat input_img,fourier_img;
	input_img = cv::imread(argv[1],cv::IMREAD_GRAYSCALE);
	if(input_img.empty()) {
		fprintf(stderr,"Could not Open image\n\n");
		return -1;
	}

	showImg(input_img,"Input Image");

	fourier_img = fourier_transform(input_img);
	showImg(fourier_img,"Fourier Image");
	cv::waitKey();
	return 0;
}

void showImg(cv::Mat& img,const std::string& name)
{

	cv::namedWindow(name.c_str());
	cv::imshow(name.c_str(),img);

}

void expand_img_to_optimal(cv::Mat& padded,cv::Mat& img) {
	int row = cv::getOptimalDFTSize(img.rows);
	int col = cv::getOptimalDFTSize(img.cols);
	cv::copyMakeBorder(img,padded,0,row - img.rows,0,col - img.cols,cv::BORDER_CONSTANT,cv::Scalar::all(0));
}


cv::Mat fourier_transform(cv::Mat& img) {
	cv::Mat padded;
	expand_img_to_optimal(padded,img);

	// Since the result of Fourier Transformation is in complex form we make two planes to hold  real and imaginary value
	cv::Mat planes[] = {cv::Mat_<float>(padded),cv::Mat::zeros(padded.size(),CV_32F)};
	cv::Mat complexI;
	cv::merge(planes,2,complexI);

	cv::dft(complexI,complexI,cv::DFT_COMPLEX_OUTPUT); // Fourier Transform

	cv::split(complexI,planes);
	cv::magnitude(planes[0],planes[1],planes[0]);
	cv::Mat magI = planes[0];

	magI += cv::Scalar::all(1);
	cv::log(magI,magI);

	crop_and_rearrange(magI);

	cv::normalize(magI, magI, 0, 1, cv::NORM_MINMAX); // for visualization purposes
	return magI;
}

void crop_and_rearrange(cv::Mat& magI)
{
	  magI = magI(cv::Rect(0, 0, magI.cols & -2, magI.rows & -2));
    int cx = magI.cols/2;
    int cy = magI.rows/2;
		cv::Mat q0(magI, cv::Rect(0, 0, cx, cy));
		cv::Mat q1(magI, cv::Rect(cx, 0, cx, cy));  // Top-Right
    cv::Mat q2(magI, cv::Rect(0, cy, cx, cy));  // Bottom-Left
    cv::Mat q3(magI, cv::Rect(cx, cy, cx, cy)); // Bottom-Right
    cv::Mat tmp;                           // swap quadrants (Top-Left with Bottom-Right)
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3)
    q1.copyTo(tmp);                    // swap quadrant (Top-Right with Bottom-Left)
    q2.copyTo(q1);
    tmp.copyTo(q2);

}

2.4 C++代码解析

上面的代码显示了傅里叶变换的幅度图像。数字图像是离散的，这表明它们具有从域值中获取值的能力。例如，简单灰度图像中的值通常介于 0 和 255 之间。因此，傅里叶变换也必须是离散的，从而产生离散傅里叶变换 (DFT)。

expand_img_to_optimal()

图像的大小对 DFT 的性能有影响。对于数字二、三和五倍数的图像大小，它是最快的。因此，为图像填充边框值以创建具有此类品质的尺寸通常是获得最大效率的好主意。我们可以使用copyMakeBorder()函数来扩展图像的边框（附加像素初始化为零）：getOptimalDFTSize()返回这个最佳尺寸，我们可以使用该copyMakeBorder()函数来扩展图像的边框。

• 为复数和实数值创建两个平面

    cv::Mat planes[] = {cv::Mat_<float>(padded),cv::Mat::zeros(padded.size(),CV_32F)};
	cv::Mat complexI;
	cv::merge(planes,2,complexI);

傅立叶变换产生复数输出。这意味着每个原图像位置输出两个图像值。此外，频域的数值范围远大于空间域的数值范围。因此，我们通常将它们保存为浮点格式。我们将更改输入图像的类型并添加另一个通道来承载复数值。

• 将实数和复数转换为幅度

  复数有两部分：实数（Re）和复数（虚数 - Im）。因此，DFT 会产生复数。如下所示：

  	cv::split(complexI,planes);
  	cv::magnitude(planes[0],planes[1],planes[0]);
  	cv::Mat magI = planes[0];
  

  傅立叶系数的动态范围太大而无法在屏幕上显示。我们有一些我们无法以这种方式看到的大小变化变量。结果，高值将全部显示为白点，而低值将显示为黑色。我们可以将线性比例转换为对数比例，以使用灰度值进行可视化：

  	magI += cv::Scalar::all(1);
  	cv::log(magI,magI);
  

crop_and_rearrange(cv::Mat& )

还记得我们在第一步中是如何扩展图像的吗？现在是时候丢弃新插入的值了。我们还可以重新排列结果的象限以进行显示，以便原点（零，零）对应于图像中心。

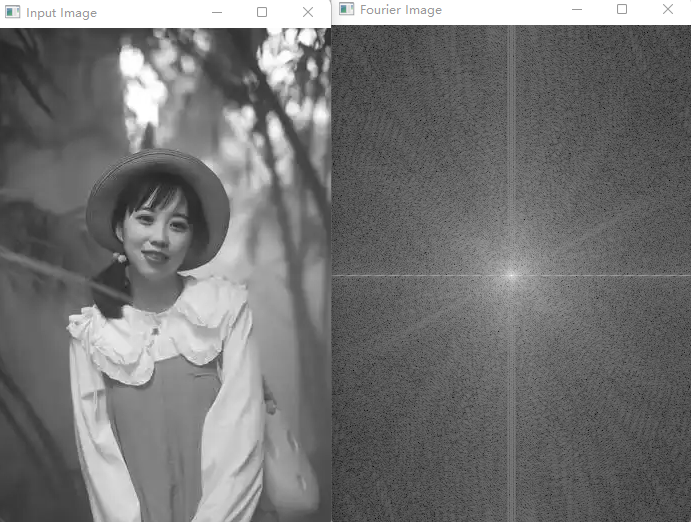
参考目录

https://anothertechs.com/programming/cpp/opencv-fourier-transform-cpp/