剑指 Offer II 091. 粉刷房子

点击查看：粉刷房子

---

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。
例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。
请计算出粉刷完所有房子最少的花费成本。

示例 1：
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

题目解析

cost数组的横坐标 代表 N号房子，纵坐标 代表 颜色
在每号房子中分别选取一种颜色，但是相邻之间不能选取相同的颜色，求最小花费

---

相邻之间不能选取相同的颜色，所以在0号房子选取蓝色后，1号房子并不能选取蓝色，
同样在1号房子选取绿色后，2号房子不能选取绿色
最小花费为 2+5+3=10

状态转移方程

到达i位置的时候，共有三种情况，下标为0时为红色，下标为1时为蓝色，下标为2时为绿色

dp[i][0]：表示粉刷到i位置的时候，最后一个位置粉刷上红色，此时的最小花费
dp[i][1]：表示粉刷到i位置的时候，最后一个位置粉刷上蓝色，此时的最小花费
dp[i][2]：表示粉刷到i位置的时候，最后一个位置粉刷上绿色，此时的最小花费

---

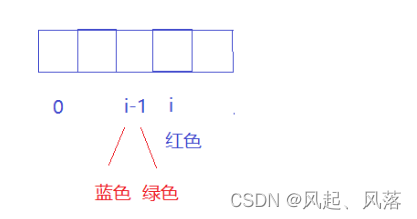
当i位置被粉刷为红色时，若想求 [0,i]区间内的 最小花费 ，就应该先求[0,i-1] 区间内的最小花费
因为相邻房子之间不能取相同的颜色，所以i-1位置只能取 蓝色或者绿色
若i-1位置为蓝色，则[0,i-1]区间的最小花费为 dp[i-1][1]
若i-1位置为绿色，则[0,i-1]区间内的最小花费为 dp[i-1][2]
取两者的最小值 ，再加上i位置的花费 即为[0,i]区间内的花费

状态转移方程为：
dp[i][0]= min(dp[i-1][1],dp[i-1][2])+costs[i][0];

---

当i位置被粉刷为蓝色时，若想求 [0,i]区间内的 最小花费 ，就应该先求[0,i-1] 区间内的最小花费
因为相邻房子之间不能取相同的颜色，所以i-1位置只能取 红色或者绿色
若i-1位置为红色，则[0,i-1]区间的最小花费为 dp[i-1][0]
若i-1位置为绿色，则[0,i-1]区间内的最小花费为 dp[i-1][2]
取两者的最小值 ，再加上i位置的花费 即为[0,i]区间内的花费

状态转移方程为：
dp[i][1]= min(dp[i-1][0],dp[i-1][2])+costs[i][1];

---

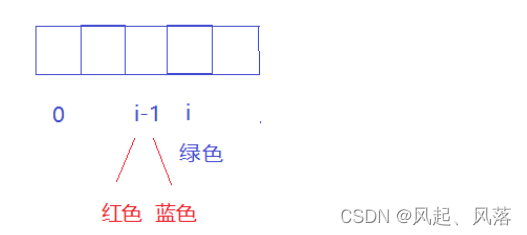
当i位置被粉刷为绿色时，若想求 [0,i]区间内的 最小花费 ，就应该先求[0,i-1] 区间内的最小花费
因为相邻房子之间不能取相同的颜色，所以i-1位置只能取 红色或者蓝色
若i-1位置为红色，则[0,i-1]区间的最小花费为 dp[i-1][0]
若i-1位置为绿色，则[0,i-1]区间内的最小花费为 dp[i-1][1]
取两者的最小值 ，再加上i位置的花费 即为[0,i]区间内的花费

状态转移方程为：
dp[i][2]= min(dp[i-1][0],dp[i-1][1])+costs[i][2];

完整代码

class Solution {
public:
    int minCost(vector<vector<int>>& costs) {
             
             int n=costs.size();
             //扩列 一行
             // 将 n+1个 vector数组 的3个数 都初始化为0
            vector<vector<int>>dp(n+1,vector<int>(3,0));
            int i=0;
            for(i=1;i<=n;i++)
            {
                //状态转移方程
                  dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i-1][0];
                  dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i-1][1];
                  dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i-1][2];
            }
            //返回 最后一次粉刷 三种颜色 其中的最小花费
            return min(min(dp[n][0],dp[n][1]),dp[n][2]);
    }
};

---

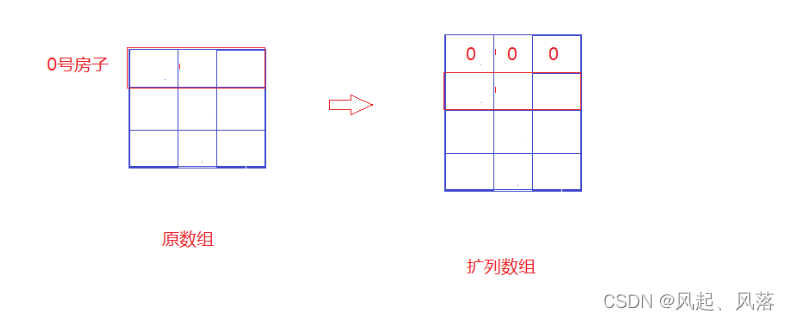
初始化
使用状态转移方程，当i为0时，会发生越界访问的情况，所以扩列一行
i为0时 即 0号房子的粉刷为红/蓝/绿色后，此时的最小花费
由于0号房子为最开始的地方，所以最小花费就为costs数组对应的元素
将扩列的一行 都置为0 即可

粉刷完最后一个房子时，算作一次花费记录，
所以比较最后一次粉刷红/蓝/绿 三种颜色 的花费的最小值 即为 最小花费

309. 最佳买卖股票时机含冷冻期

点击查看：最佳买卖股票时机含冷冻期

---

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0

题目解析

若买入一支股票，卖出后，就会进入冷冻期，什么都做不了
最后上述最大利润 为 3

状态转移方程

dp[i]：表示第i天结束时，所能拿到的最大利润
在i位置处共有四种状态： 持有股票 保持卖出股票 冷冻期 卖出股票
将 持有股 状态 用下标0表示 ，将保持卖出股票 状态 用下标1表示 ，将卖出股票状态用下标2表示，将冷冻期 用下标3表示
即 dp[i][0] 持有股票 dp[i][1]保持卖出股票 dp[i][2]卖出股票 dp[i][3] 冷冻期

dp[i][0]：表示第i天结束后，处于 持有股票 状态，此时的最大利润
dp[i][1]：表示第i天结束后，处于 保持卖出股票 状态，此时的最大利润
dp[i][2]：表示第i天结束后，处于 卖出股票 状态，此时的最大利润
dp[i][3]：表示第i天结束后，处于 冷冻期 状态，此时的最大利润

在冷冻期之前将股票卖出，在冷冻期之后，什么都不干，则一直保持卖出股票的状态

持有股票

若第i-1天为持有股票状态，第i天延续第i-1天的状态
该情况下 ：dp[i][0]=dp[i-1][0]

---

若第i-1天是冷冻期，第i天为买入股票状态
从第i-1天到第i天，还需减去股票价格
该情况下 ：dp[i][0]=dp[i-1][3]-price[i]

---

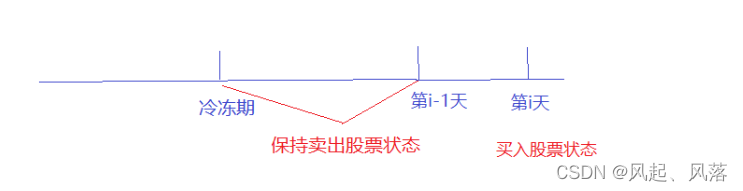
从冷冻期结束，一直到到第i-1天，都保持卖出股票状态，第i天为买入股票状态
该情况下 ：dp[i][0]=dp[i-1][1]-price[i]

---

将三者取最大值
状态转移方程为：
dp[i][0]= max ( max(dp[i-1][0],dp[i-1][3]-price[i]) ,dp[i-1][1]-price[i]);

保持卖出股票

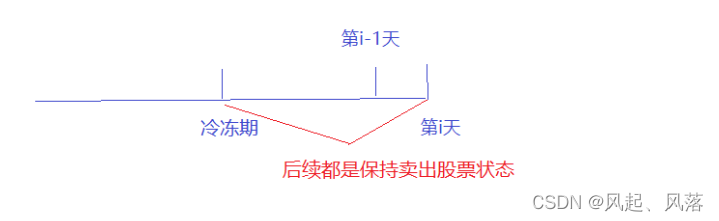
若第i天想要为 保持卖出股票状态，则第i-1天可以为 保持卖出股票状态
该情况下 ：dp[i][1]= dp[i-1][1]

---

若第i天想要为 卖出股票状态，则第i-1天可以为 冷冻期 状态
该情况下： dp[i][1]=dp[i-1][3]

---

取两者最大值
状态转移方程：
dp[i][1]=max(dp[i-1][1],dp[i-1][3]);

卖出股票

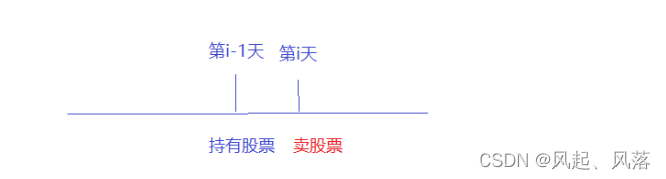
第i-1天持有股票，第i天卖股票
从第i-1天到第i天，还需加上股票价格

状态转移方程为：
dp[i][2]= dp[i-1][0]+price[i];

冷冻期

第i-1天卖股票状态，第i天为冷冻期状态

状态转移方程为：
dp[i][3] = dp[i-1][2];

完整代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
     int n=prices.size();
     int i=0;
     vector<vector<int>>dp(n,vector<int>(4,0));
     //将股票买了，需要花钱 所以利润为负
     dp[0][0]=-prices[0];
     for(i=1;i<n;i++)
     {
         //持有股票
         dp[i][0]= max( max(dp[i-1][0],dp[i-1][3]-prices[i]),
         dp[i-1][1]-prices[i]);

         //保持卖出股票
         dp[i][1]= max(dp[i-1][1],dp[i-1][3]);

         //卖出股票
         dp[i][2]=dp[i-1][0]+prices[i];

         //冷冻期
         dp[i][3]= dp[i-1][2];
     }
     //最后一天 若买入 则不会获得最大利润 ，所以去除下标为0的情况
     return max(max(dp[n-1][1],dp[n-1][2]),dp[n-1][3]);
    }
};

714. 买卖股票的最佳时机含手续费

点击查看：买卖股票的最佳时机含手续费

---

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：
输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

题目解析

当数组元素值为1时，买入股票，由于在卖出股票时要支付小费2元，所以在 数组元素值为3 或2 时 ，卖出都是不合算的
在数组元素值为8时，卖出股票，8-1-2=5
在数组元素值为4时，买入股票 ，在数组元素值为9时，卖出股票，9-4-2=3
最大利润为：5+3=8

状态转移方程

dp[i]：表示 第i天结束后，所能获得的最大利润

---

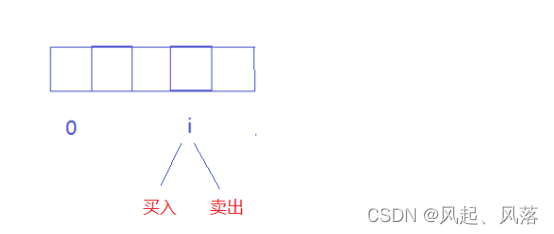
在i位置处，共有两种状态 ，买入状态和卖出状态

f[i]：表示 第i天结束后，处于买入 状态，此时的最大利润
g[i]：表示第i天结束后，处于卖出 状态，此时的最大利润

---

仅需支付一次手续费,假设在卖出股票时加上手续费

f[i]状态转移方程

若第i-1天处于买入状态，第i天啥也不干，则第i天也处于买入状态
该情况下：f[i]=f[i-1]

---

若第i-1天处于卖出状态，则第i天处于买入状态
需要减去买股票对应的花费 price[i]
该情况下：f[i]=g[i-1]-price[i]

状态转移方程为：
f[i] =max(f[i-1],g[i-1]-price[i]);

g[i]状态转移方程

若第i-1天卖出状态，第i天啥也不干，则第i天也处于卖出状态
该情况下：g[i]=g[i-1]

---

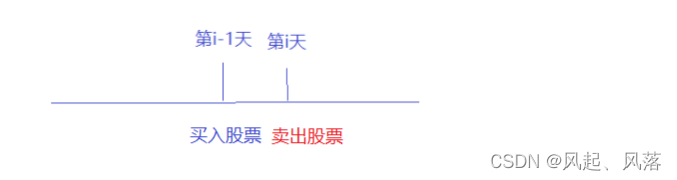
若第i-1天处于买入状态，则第i天处于卖出状态
需要加上卖股票对应的利润 price[i]，同时卖出股票还需手续费
该情况下：g[i]=f[i-1]+price[i]-fee

状态转移方程为：
g[i]= max(g[i-1],f[i-1]+price[i]-fee);

完整代码

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n=prices.size();
        int i=0;
        //f表示 买入  g表示卖出
        vector<int>f(n,0);
        vector<int>g(n,0);
        //将股票买了，需要花钱,所以利润为负
        f[0]=-prices[0];
        g[0]=0;
        for(i=1;i<n;i++)
        {
            f[i]=max(f[i-1],g[i-1]-prices[i]);
            g[i]=max(g[i-1],f[i-1]+prices[i]-fee);
        }
        //在最后一个位置处  在买股票对应的利润肯定是没有将股票卖出的利润多的
        return g[n-1];
    }
};