文章目录
- 归并排序
- 归并排序的思想
- 单趟排序的实现
- 归并排序实现
- 非递归版本的实现
- 特性总结
- 计数排序
- 计数排序的思想
- 计数排序的实现
- 特性总结
归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列。即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
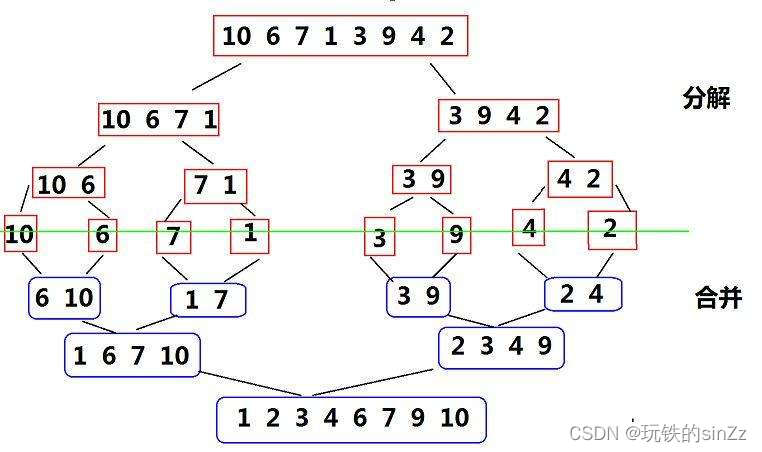
归并排序的思想
首先,要开辟一个长度和待排序数组一样的临时数组,用于存储归并操作后的数据。一、将带排序的数据区间不断二分,直到区间内只有一个数据或区间不存在。通过递归对每个子区间进行归并,把归并的序列写入到临时数组中,最后将归并好的内容从临时数组拷贝回原数组。
单趟排序的实现
首先,对两个区间的内容的较小值写入tmp数组中以达到区间归并。当一个区间的数组全部写入完毕,那么将剩下的一个区间的内容直接尾插到临时数组中。最后,用memcpy将临时数组内容拷贝回原数组中。
void _MergeSort(int* arr, int begin, int end, int* tmp)
{
int mid = (end + begin) / 2;
//子区间归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
//把剩下的直接尾插到tmp数组中
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//将归并的内容拷回原数组
memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
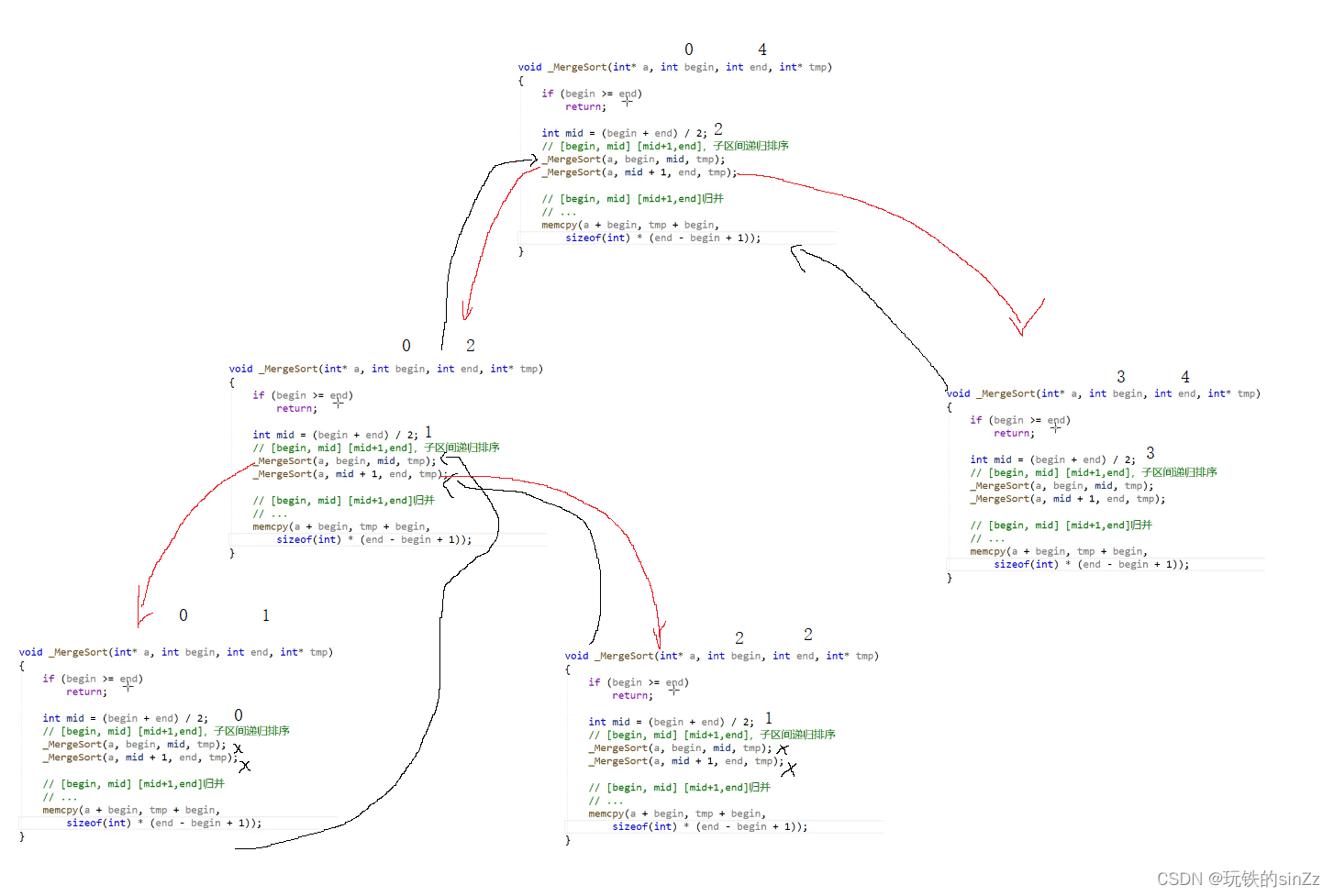
归并排序实现
就是在单趟排序的基础上递归对于区间进行划分,直到区间不存在开始进行归并。当然画递归展开图也能有助于我们理解归并排序的递归实现。

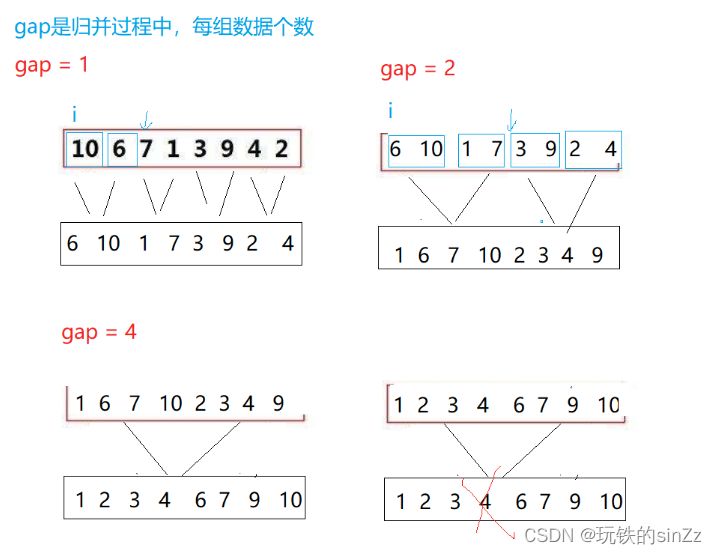
非递归版本的实现
实现思路如下:将递归改成非递归,其实类似于斐波那契数列的递归改非递归问题。不过这里的归并的思路我们需要从11归并到22归并到44归并。首先,先开辟临时数组。然后,将从1开始进行归并的数据。最后,单趟排序思路如上,这里不做赘述。
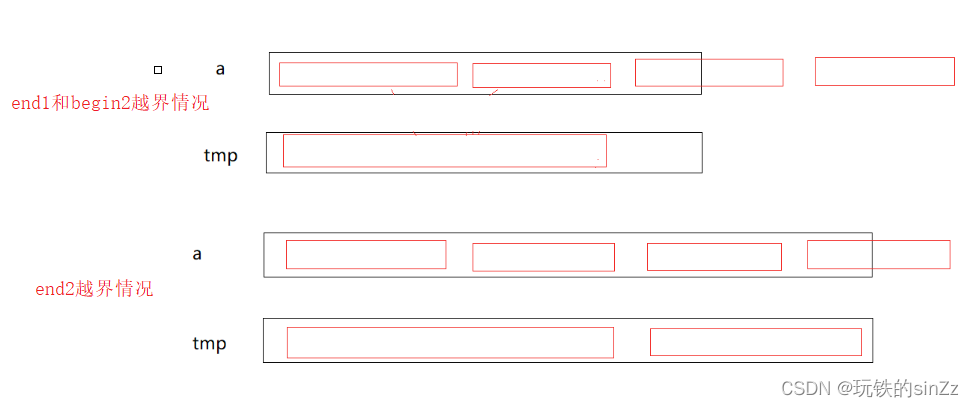
由于数据不可能每次都是完美的二分,所以我们需要对区间进行讨论。begin1肯定是不会越界的。end1,begin2,end2都是存在越界可能的。这里我们已多组拷贝的形式来进行。当end1和begin2越界时,我们直接跳出循环,不做处理。当end2越界时,将end2修正成数组长度-1的下标值。
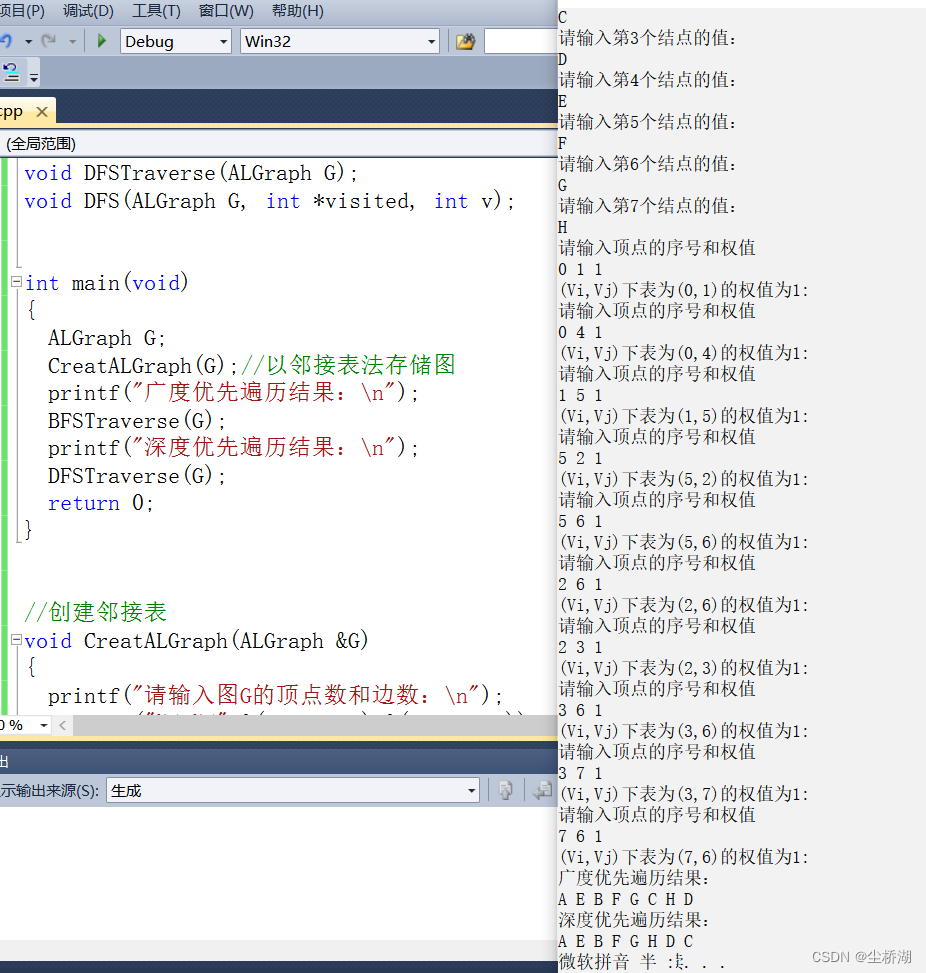
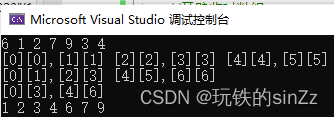
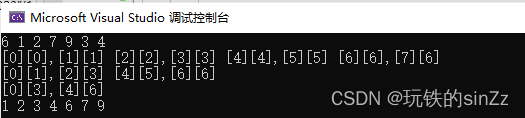
下面我就以每组归并完然后拷贝的形式的代码先演示一下。

下面我将每组区间的值打印出来方便看。
这是以多组归并后拷贝的方式进行的。当然这不是唯一的方式 ,下面我介绍一下一把梭哈拷贝的方式要怎么处理边界的问题。
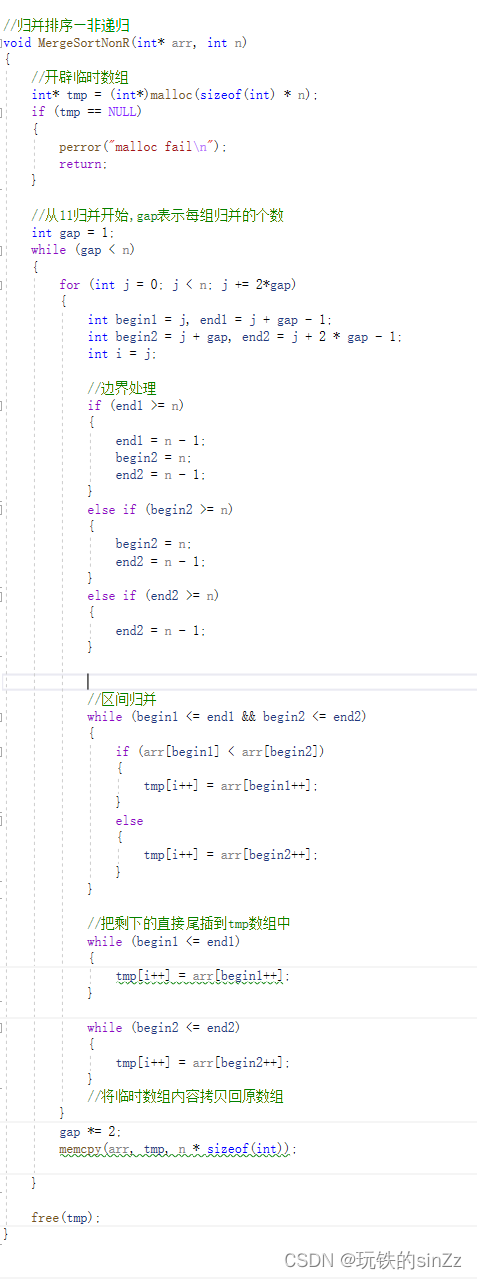
由于是一把梭哈拷贝,所以要对越界区间进行修饰。然后我把修饰后的值打出来看。
特性总结
一、归并排序的时间复杂度为O(N*LogN),空间复杂度为O(N)。
二、归并排序可以解决在磁盘中的外排序问题。因为有时候在海量的数据下进行排序,内存可能容纳不下,就只能放在磁盘中进行排序。归并排序可以用递归的角度去遍历文件系统。类似的快速排序和堆排序却不能达到这种效果。因为文件系统属于树形结构,对于数组存储的堆和左右指针遍历数组的快速排序都不适合。
三、归并排序是一个稳定的排序。
计数排序
计数排序和前面介绍的有着本质的不同。它属于非比较排序的一种。前面我们介绍的都是比较排序,即值的大小来做比较。
计数排序的思想
根据数组最大值最小值的范围进行相对映射来进行计数,然后遍历技术数组,将相对映射的值重新写回原数组以达到排序的功能。
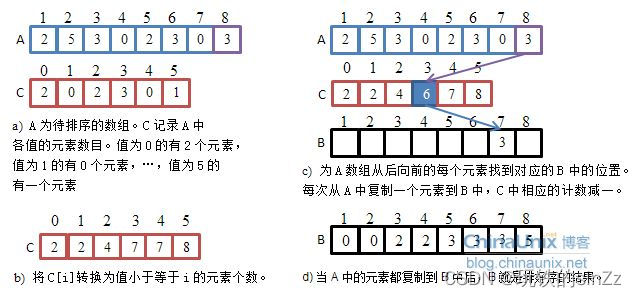
计数排序的实现
首先,遍历数组求出最大值和最小值,根据最大值和最小值求出数组值得范围,开辟一个长度为最大值-最小值+1的数组来计数,根据值的相对映射来进行计数,然后遍历技术数组,将相对映射的值重新写回原数组以达到排序的功能。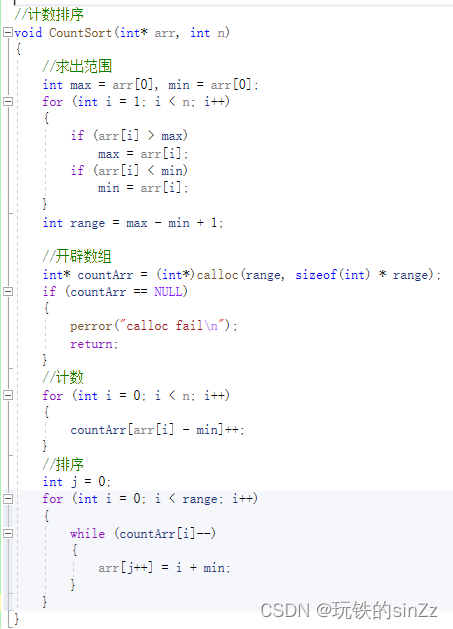
特性总结
一、计数排序是一个只适用于排序数据范围集中的整型数据。应用场景比较有限。绝对映射是不适合的,因为在有负整数的场景下会无法进行计数。以及在数值较大,数值间差值范围较小的情况下,空间损耗过大。所以采取相对映射比较合适。
二、时间复杂度为O(N+range),空间复杂度为O(range)。