无向图G的广度优先搜索和深度优先搜索以及完整程序

news2024/11/18 6:31:49

图的遍历算法有两种：广度优先搜索和深度优先搜索

一.广度优先搜索类似于层次遍历，需要借助辅助队列

空间复杂度为O(|V|);空间复杂度由辅助队列大小决定

时间复杂度为O(|V|+|E|)

为避免同一顶点被多次访问，设计visited[]来标记顶点

二.深度优先搜索类似于树的先序遍历，递归算法

空间复杂度：最好O(1),最坏O(|V|);

时间复杂度：O(|V|+|E|);

时间复杂度 = 访问各结点所需时间+探索各条边所需时间

对于无向图进行BFS/DFS遍历：调用BFS/DFS函数的次数 = 连通分量数；对于连通图只需要调用1次BFS/DFS函数。

对于有向图进行BFS/DFS遍历：调用BFS/DFS函数的次数要具体问题具体分析；若起始顶点到其他顶点都有路径，只需要调用1次BFS/DFS函数；对于强连通图，从任一顶点出发都只需要调用1次BFS/DFS函数。

三.邻接矩阵存储图进行广度优先搜索和深度优先搜索

权值设置的都为1，可自行设置

圆圈内为顶点的值，上面为其序号；一该图为例进行邻接矩阵存储 

1.先创造邻接矩阵存储图

1.1图的结构体构造

typedef char VerTexType;//顶点的数据类型
typedef int EdgeType;//带权图中边上权值数据类型
typedef struct
{
  VerTexType Vex[MaxVertexNum];//顶点表
  EdgeType Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵，边表
  int vexnum,arcnum;//图的当前顶点数和弧数
}MGraph;

1.2无向图邻接矩阵构造

//1.无向网的建立
void CreatMGraph(MGraph &G)
{
  printf("请输入图的顶点数和边数：");
  int m,n;
  scanf_s("%d %d",&m,&n);
  G.vexnum = m;
  G.arcnum = n;
  char val;
  for(int i = 0; i < G.vexnum; ++i)
  {
	  printf("第%d个顶点值为:",i);
	  scanf_s("%*c%c",&val);
	  G.Vex[i] = val;
  }
  for(int i = 0; i < G.vexnum; ++i)
  { 
	  for(int j = 0; j < G.vexnum; ++j)
	  {
		  G.Edge[i][j] = Max;
	  }
  }
  int i,j,w;
  for(int k = 0; k < G.arcnum; ++k)
  {
	printf("请输入顶点和权值\n");
	scanf_s("%d %d %d",&i,&j,&w);
    printf("(Vi,Vj)下表为(%d,%d)的权值为%d:\n",i,j,w);
	G.Edge[i][j] = w;
	G.Edge[j][i] = G.Edge[i][j];
  }

}

1.3FirstNeighbor函数构造

//2.求图G中顶点编号x的第一个邻接点
int FirstNeighbor(MGraph G, int x)
{

	for(int j = 0; j < G.vexnum; ++j)
	{
		if(G.Edge[x][j] != -1)
			return j;
	}
	return -1;
}

1.4NextNeighbor函数构造

//3.假设图G中顶点y是顶点x的一个邻近点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1
int NextNeighbor(MGraph G, int x, int y)
{
  for(int j = y+1; j < G.vexnum; ++j)
  {
	  if(G.Edge[x][j] != -1)
		  return j;
  }
  return -1;
}

2.广度优先搜索的构造辅助队列

2.1辅助队列结构体

//定义队列的结构体
typedef struct LinkNode
{
  int data;//队列的数据域
  LinkNode *next;//指针域
}LinkNode;

typedef struct
{
  LinkNode *front;//队列对头指针
  LinkNode *rear;//队列队尾指针
}LinkQueue;

2.1初始化队列

//1.初始化
void InitQueue(LinkQueue &Q)
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	Q.rear->next = NULL;
}

2.2入队函数

//2.入队
void EnQueue(LinkQueue &Q, int x)
{
  LinkNode *p = (LinkNode*)malloc(sizeof(LinkNode));
  if(p == NULL)
  {
    printf("动态内存分配失败！");
	exit(-1);
  }
  p->data = x;
  //通过尾插法入队
  p->next = NULL;
  Q.rear->next = p;
  Q.rear = p;
}

2.3出队函数

//3.出队
int DeQueue(LinkQueue &Q,int &x)
{
  if(IsEmpty(Q))
	  return -1;
  else
  {
	  LinkNode *p = Q.front->next;
	  x = p->data;
	  Q.front->next = p->next;
	  if(Q.rear == p)
		  Q.rear = Q.front;
	  free(p);
  }
  return x;
}

2.4判断队列为空

//4.判断空
bool IsEmpty(LinkQueue Q)
{
	if(Q.front == Q.rear)
	{
	  return true;
	}
	else
	{
	  return false;
	}
}

3.广度优先搜索

权值设置的都为1，可自行设置

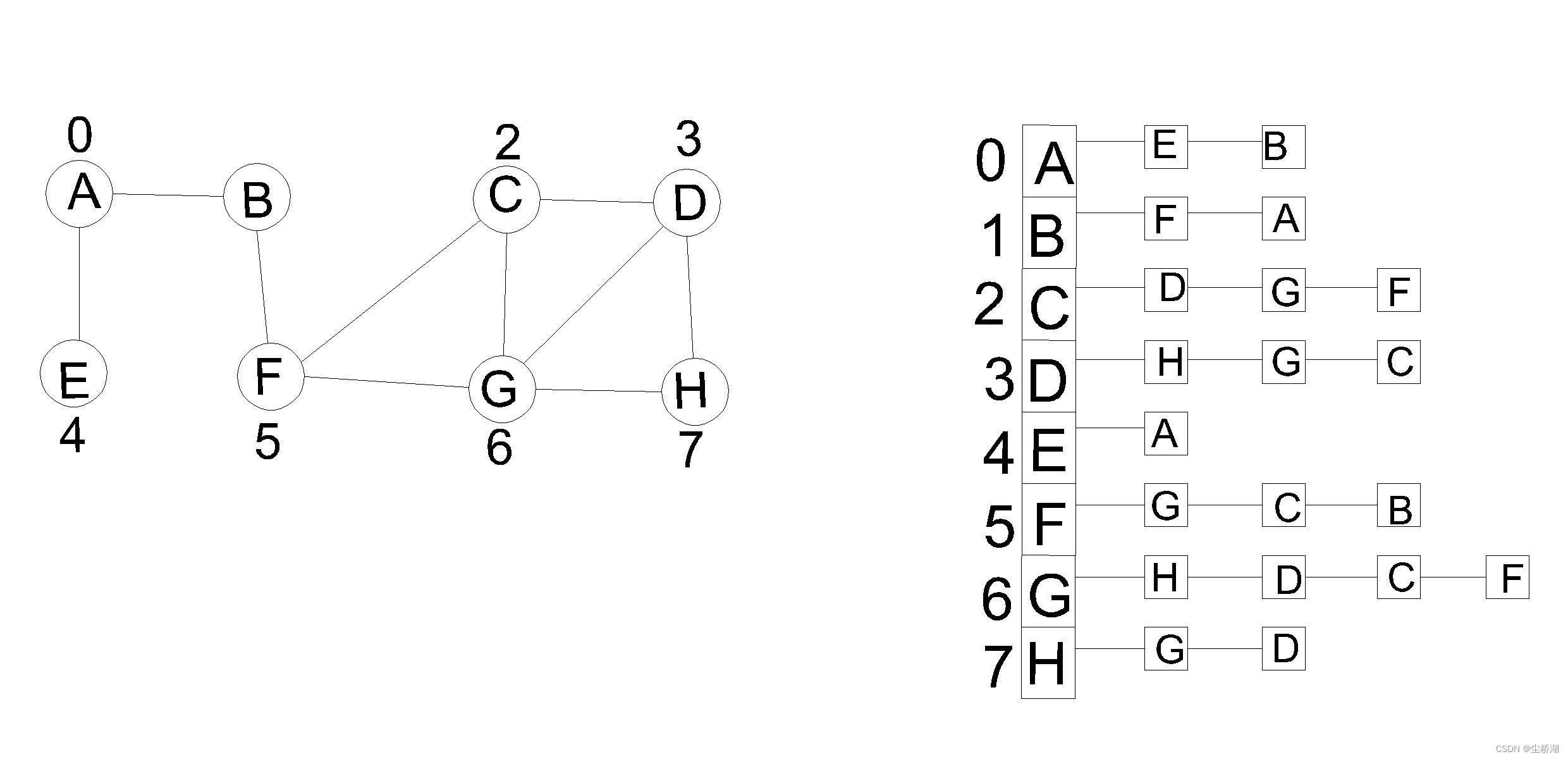
以该例子进行邻接表存储 

3.1广度优先遍历图G

//广度优先搜索
//1.对图G进行广度优先遍历
void BFSTraverse(MGraph G)
{
	int *visited;
	visited = (int *)malloc(sizeof(int)*G.vexnum);
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;
	}
	for(int i = 0; i < G.vexnum; ++i)
	{//从0号顶点遍历
	  if(!visited[i])//如果visited[i] == 0表示该点还未被访问
		  BFS(G,visited,i);//每个连通分量调用一次BFS函数
	}
	printf("\n");
}

3.2广度优先遍历

//2.广度优先遍历
void BFS(MGraph G,int *visited,int v)
{
	printf("%c ",G.Vex[v]);//打印输出初始顶点
	visited[v] = 1;//将打印过的顶点标记为true
	LinkQueue Q;
	InitQueue(Q);
	EnQueue(Q,v);//将顶点入队
	while(!IsEmpty(Q))//判断队列是否为空
	{
	  int u = DeQueue(Q,v);//不为空则出队
	  for(int w = FirstNeighbor(G,u); w >= 0; w = NextNeighbor(G,u,w))
	  {//检查序号v所有的邻接点
	    if(!visited[w])//如果序号为w的顶点还未被访问
		{
			printf("%c ",G.Vex[w]);
			visited[w] = 1;//将打印输出顶点的序号标记为1表示已经被访问
			EnQueue(Q,w);//将顶点入队
		}
	  }
	}

}

4.深度优先搜索

4.1深度优先遍历图G

//1.对图G进行深度优先遍历
void DFSTraverse(MGraph G)
{
	int *visited = (int *)malloc(sizeof(int)*G.vexnum);//创造标记组
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;//等于0表示还未被访问，以免因为图中环的存在导致重复遍历
	}
	for(int i = 0; i < G.vexnum; ++i)//如果图中不止一个连通分量，可以将其全部遍历输出
	{
	  if(!visited[i])
		  DFS(G,visited,i);
	}
}

4.2深度优先遍历

//2.深度优先遍历
void DFS(MGraph G, int *visited, int v)
{
	printf("%c ",G.Vex[v]);//遍历输出顶点的值
	visited[v] = 1;//将该顶点的标记值改为1，表示该顶点已经被访问
	for(int w = FirstNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w))
	{
	  if(!visited[w])
		  DFS(G,visited,w);
	}

}

5.运行结果

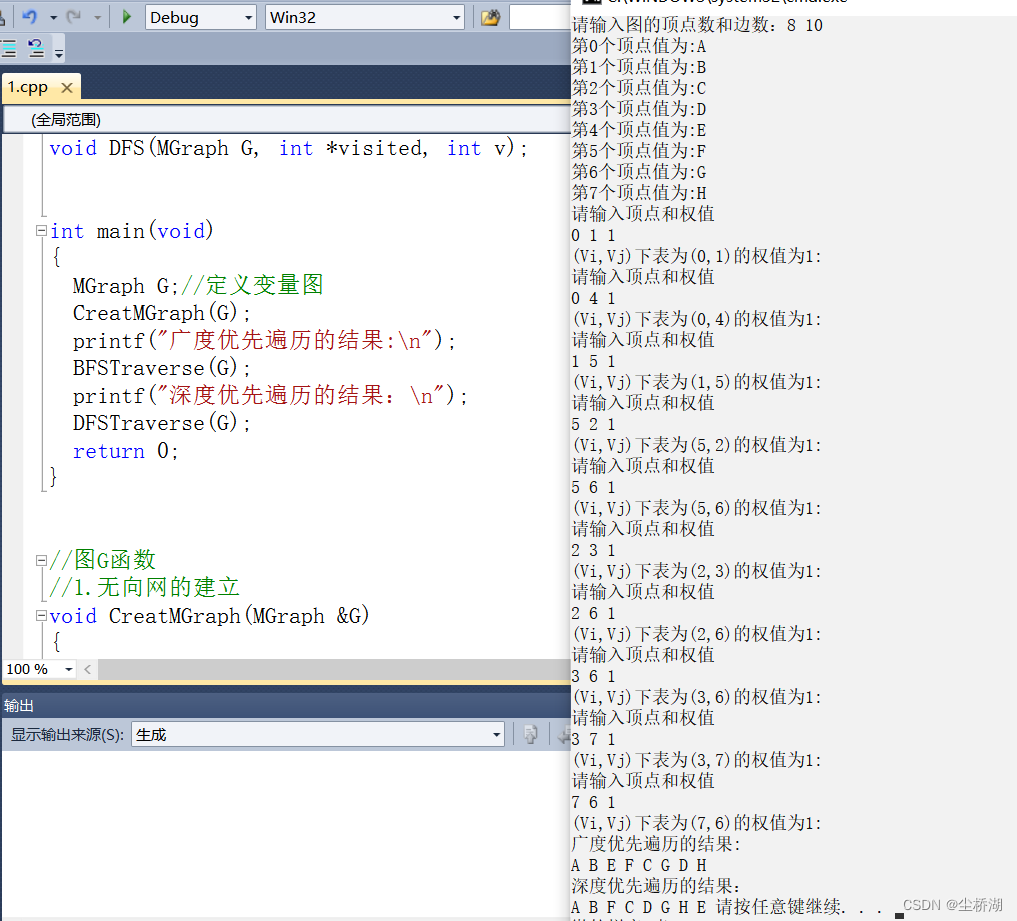
四.无向图G邻接矩阵存储广度优先搜索和深度优先搜索

1.先创造邻接表 

1.1邻接表的结构体

#define MaxVertexNum 10//图中顶点数目的最大值
typedef char VertexType;
//邻接表的结构体
//定义边表结点
typedef struct ArcNode
{
  int adjvex;//该弧所指向的顶点的位置
  struct ArcNode *next;//指向下一条弧的指针
  int info;//网的边权值
}ArcNode;

//顶点表信息，用顺序结构存储顶点表的信息
typedef struct VNode
{
  VertexType data;//顶点信息
  ArcNode *first;//指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];

//邻接表
typedef struct
{
  AdjList vertices;//邻接表
  int vexnum,arcnum;//图的顶点数和弧数
}ALGraph;//ALGraph是以邻接表存储图的类型

 1.2创造邻接表

//创建邻接表
void CreatALGraph(ALGraph &G)
{
  printf("请输入图G的顶点数和边数：\n");
  scanf_s("%d %d",&(G.vexnum),&(G.arcnum));
  //输入结点
  char val;
  for(int i = 0; i < G.vexnum; ++i)
  {
    printf("请输入第%d个结点的值：\n",i);
	scanf_s("%*c%c",&val);
	G.vertices[i].data = val;
	G.vertices[i].first = NULL;//最开始令每个顶点的第一条依附顶点的弧的指针为空
  }
  //输入边
  int i,j,w;
  for(int k = 0; k < G.arcnum; ++k)
  {
	ArcNode *m = (ArcNode*)malloc(sizeof(ArcNode));
	printf("请输入顶点的序号和权值\n");
	scanf_s("%d %d %d",&i,&j,&w);
    printf("(Vi,Vj)下表为(%d,%d)的权值为%d:\n",i,j,w);
	m->adjvex = j;
	m->info = w;
	//用头插法创造边表
	m->next = G.vertices[i].first;
	G.vertices[i].first = m;
	//这个是无向图，而且令k<G.arcnum，因为一个弧对应两个顶点，两个顶点都是顶点表中的，所以要同时将两个顶点表的边表都弄好
	ArcNode *n = (ArcNode*)malloc(sizeof(ArcNode));
	n->adjvex = i;
	n->info = w;
	//用头插法创建边表
	n->next = G.vertices[j].first;
	G.vertices[j].first = n;
  }

}

1.3FirstNeighbor函数

//求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1.
int FirstNeighbor(ALGraph G, int x)
{
	if(x >= G.vexnum)
	{
	  return -1;
	}
	else if(G.vertices[x].first == NULL)
	{	
	  return -1;
	}
	else
	{
		ArcNode *p = G.vertices[x].first;//指向图G的顶点x的邻接点的指针
		int i = p->adjvex;//邻接点的序号
		return i;
	}

}

1.4NextNeighbor函数

//假设图G中顶点y是顶点x的一个邻接点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1
int NextNeighbor(ALGraph G,int x,int y)
{
	ArcNode *p = G.vertices[x].first;
	while(p->adjvex != y)
	{
		p = p->next;
	}
	if(p->next == NULL)
	{
		return -1;
	}
	else
	{
		p = p->next;
		int j = p->adjvex;
		return j;
	}
}

2.队列和上面一致，这里就不在展示代码

3.广度优先搜素和深度优先搜素和上面也是一致的，结尾有完整代码可以观看

4.运行结果：

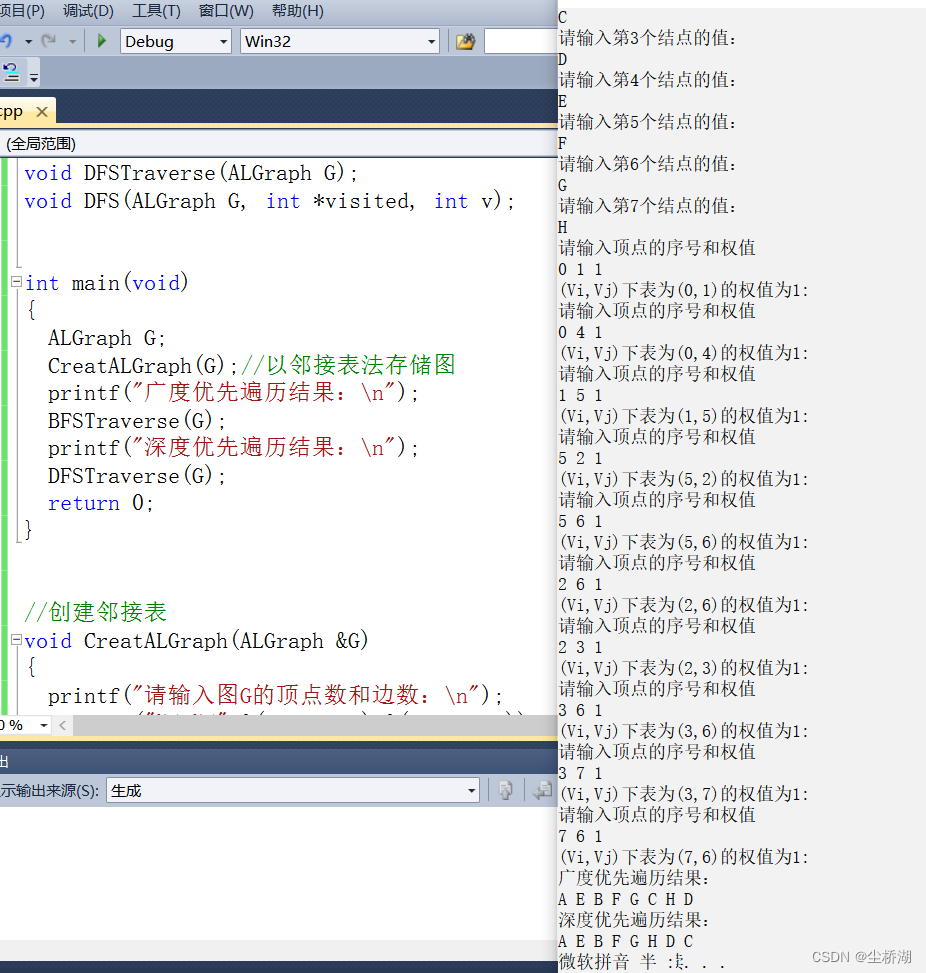
 五.完整程序

1.以邻接矩阵存储进行广度优先和深度优先搜索

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#define Max -1//这里以-1代表最大值
#define MaxVertexNum 15


typedef char VerTexType;//顶点的数据类型
typedef int EdgeType;//带权图中边上权值数据类型
typedef struct
{
  VerTexType Vex[MaxVertexNum];//顶点表
  EdgeType Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵，边表
  int vexnum,arcnum;//图的当前顶点数和弧数
}MGraph;


//定义队列的结构体
typedef struct LinkNode
{
  int data;//队列的数据域
  LinkNode *next;//指针域
}LinkNode;

typedef struct
{
  LinkNode *front;//队列对头指针
  LinkNode *rear;//队列队尾指针
}LinkQueue;



//图G的函数说明
void CreatMGraph(MGraph &G);
int FirstNeighbor(MGraph G, int x);
int NextNeighbor(MGraph G, int x, int y);


//队列的函数说明
void InitQueue(LinkQueue &Q);
void EnQueue(LinkQueue &Q, int x);
int DeQueue(LinkQueue &Q,int &x);
bool IsEmpty(LinkQueue Q);


//广度优先遍历的函数说明
void BFSTraverse(MGraph G);
void BFS(MGraph G,int *visited,int v);

//深度优先遍历
void DFSTraverse(MGraph G);
void DFS(MGraph G, int *visited, int v);


int main(void)
{
  MGraph G;//定义变量图
  CreatMGraph(G);
  printf("广度优先遍历的结果:\n");
  BFSTraverse(G);
  printf("深度优先遍历的结果：\n");
  DFSTraverse(G);
  return 0;
}


//图G函数
//1.无向网的建立
void CreatMGraph(MGraph &G)
{
  printf("请输入图的顶点数和边数：");
  int m,n;
  scanf_s("%d %d",&m,&n);
  G.vexnum = m;
  G.arcnum = n;
  char val;
  for(int i = 0; i < G.vexnum; ++i)
  {
	  printf("第%d个顶点值为:",i);
	  scanf_s("%*c%c",&val);
	  G.Vex[i] = val;
  }
  for(int i = 0; i < G.vexnum; ++i)
  { 
	  for(int j = 0; j < G.vexnum; ++j)
	  {
		  G.Edge[i][j] = Max;
	  }
  }
  int i,j,w;
  for(int k = 0; k < G.arcnum; ++k)
  {
	printf("请输入顶点和权值\n");
	scanf_s("%d %d %d",&i,&j,&w);
    printf("(Vi,Vj)下表为(%d,%d)的权值为%d:\n",i,j,w);
	G.Edge[i][j] = w;
	G.Edge[j][i] = G.Edge[i][j];
  }

}

//2.求图G中顶点编号x的第一个邻接点
int FirstNeighbor(MGraph G, int x)
{

	for(int j = 0; j < G.vexnum; ++j)
	{
		if(G.Edge[x][j] != -1)
			return j;
	}
	return -1;
}

//3.假设图G中顶点y是顶点x的一个邻近点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1
int NextNeighbor(MGraph G, int x, int y)
{
  for(int j = y+1; j < G.vexnum; ++j)
  {
	  if(G.Edge[x][j] != -1)
		  return j;
  }
  return -1;
}


//队列的函数

//1.初始化
void InitQueue(LinkQueue &Q)
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	Q.rear->next = NULL;
}

//2.入队
void EnQueue(LinkQueue &Q, int x)
{
  LinkNode *p = (LinkNode*)malloc(sizeof(LinkNode));
  if(p == NULL)
  {
    printf("动态内存分配失败！");
	exit(-1);
  }
  p->data = x;
  //通过尾插法入队
  p->next = NULL;
  Q.rear->next = p;
  Q.rear = p;
}

//3.出队
int DeQueue(LinkQueue &Q,int &x)
{
  if(IsEmpty(Q))
	  return -1;
  else
  {
	  LinkNode *p = Q.front->next;
	  x = p->data;
	  Q.front->next = p->next;
	  if(Q.rear == p)
		  Q.rear = Q.front;
	  free(p);
  }
  return x;
}

//4.判断空
bool IsEmpty(LinkQueue Q)
{
	if(Q.front == Q.rear)
	{
	  return true;
	}
	else
	{
	  return false;
	}
}

//广度优先搜索
//1.对图G进行广度优先遍历
void BFSTraverse(MGraph G)
{
	int *visited;
	visited = (int *)malloc(sizeof(int)*G.vexnum);
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;
	}
	for(int i = 0; i < G.vexnum; ++i)
	{//从0号顶点遍历
	  if(!visited[i])//如果visited[i] == 0表示该点还未被访问
		  BFS(G,visited,i);//每个连通分量调用一次BFS函数
	}
	printf("\n");
}

//2.广度优先遍历
void BFS(MGraph G,int *visited,int v)
{
	printf("%c ",G.Vex[v]);//打印输出初始顶点
	visited[v] = 1;//将打印过的顶点标记为true
	LinkQueue Q;
	InitQueue(Q);
	EnQueue(Q,v);//将顶点入队
	while(!IsEmpty(Q))//判断队列是否为空
	{
	  int u = DeQueue(Q,v);//不为空则出队
	  for(int w = FirstNeighbor(G,u); w >= 0; w = NextNeighbor(G,u,w))
	  {//检查序号v所有的邻接点
	    if(!visited[w])//如果序号为w的顶点还未被访问
		{
			printf("%c ",G.Vex[w]);
			visited[w] = 1;//将打印输出顶点的序号标记为1表示已经被访问
			EnQueue(Q,w);//将顶点入队
		}
	  }
	}

}


//深度优先遍历，类似于树的先序遍历

//1.对图G进行深度优先遍历
void DFSTraverse(MGraph G)
{
	int *visited = (int *)malloc(sizeof(int)*G.vexnum);//创造标记组
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;//等于0表示还未被访问，以免因为图中环的存在导致重复遍历
	}
	for(int i = 0; i < G.vexnum; ++i)//如果图中不止一个连通分量，可以将其全部遍历输出
	{
	  if(!visited[i])
		  DFS(G,visited,i);
	}
}

//2.深度优先遍历
void DFS(MGraph G, int *visited, int v)
{
	printf("%c ",G.Vex[v]);//遍历输出顶点的值
	visited[v] = 1;//将该顶点的标记值改为1，表示该顶点已经被访问
	for(int w = FirstNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w))
	{
	  if(!visited[w])
		  DFS(G,visited,w);
	}

}

2.邻接表存储进行广度优先和深度优先搜索

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>

#define MaxVertexNum 10//图中顶点数目的最大值
typedef char VertexType;
//邻接表的结构体
//定义边表结点
typedef struct ArcNode
{
  int adjvex;//该弧所指向的顶点的位置
  struct ArcNode *next;//指向下一条弧的指针
  int info;//网的边权值
}ArcNode;

//顶点表信息，用顺序结构存储顶点表的信息
typedef struct VNode
{
  VertexType data;//顶点信息
  ArcNode *first;//指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];

//邻接表
typedef struct
{
  AdjList vertices;//邻接表
  int vexnum,arcnum;//图的顶点数和弧数
}ALGraph;//ALGraph是以邻接表存储图的类型


//定义队列的结构体
typedef struct LinkNode
{
  int data;//队列的数据域
  LinkNode *next;//指针域
}LinkNode;

typedef struct
{
  LinkNode *front;//队列对头指针
  LinkNode *rear;//队列队尾指针
}LinkQueue;



//图的函数说明
void CreatALGraph(ALGraph &G);
int FirstNeighbor(ALGraph G, int x);
int NextNeighbor(ALGraph G,int x,int y);


//队列的函数说明
void InitQueue(LinkQueue &Q);
void EnQueue(LinkQueue &Q, int x);
int DeQueue(LinkQueue &Q,int &x);
bool IsEmpty(LinkQueue Q);


//广度优先遍历函数说明
void BFSTraverse(ALGraph G);
void BFS(ALGraph G, int *visited, int v);

//深度优先遍历函数说明
void DFSTraverse(ALGraph G);
void DFS(ALGraph G, int *visited, int v);


int main(void)
{
  ALGraph G;
  CreatALGraph(G);//以邻接表法存储图
  printf("广度优先遍历结果：\n");
  BFSTraverse(G);
  printf("深度优先遍历结果：\n");
  DFSTraverse(G);
  return 0;
}


//创建邻接表
void CreatALGraph(ALGraph &G)
{
  printf("请输入图G的顶点数和边数：\n");
  scanf_s("%d %d",&(G.vexnum),&(G.arcnum));
  //输入结点
  char val;
  for(int i = 0; i < G.vexnum; ++i)
  {
    printf("请输入第%d个结点的值：\n",i);
	scanf_s("%*c%c",&val);
	G.vertices[i].data = val;
	G.vertices[i].first = NULL;//最开始令每个顶点的第一条依附顶点的弧的指针为空
  }
  //输入边
  int i,j,w;
  for(int k = 0; k < G.arcnum; ++k)
  {
	ArcNode *m = (ArcNode*)malloc(sizeof(ArcNode));
	printf("请输入顶点的序号和权值\n");
	scanf_s("%d %d %d",&i,&j,&w);
    printf("(Vi,Vj)下表为(%d,%d)的权值为%d:\n",i,j,w);
	m->adjvex = j;
	m->info = w;
	//用头插法创造边表
	m->next = G.vertices[i].first;
	G.vertices[i].first = m;
	//这个是无向图，而且令k<G.arcnum，因为一个弧对应两个顶点，两个顶点都是顶点表中的，所以要同时将两个顶点表的边表都弄好
	ArcNode *n = (ArcNode*)malloc(sizeof(ArcNode));
	n->adjvex = i;
	n->info = w;
	//用头插法创建边表
	n->next = G.vertices[j].first;
	G.vertices[j].first = n;
  }

}

//求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1.
int FirstNeighbor(ALGraph G, int x)
{
	if(x >= G.vexnum)
	{
	  return -1;
	}
	else if(G.vertices[x].first == NULL)
	{	
	  return -1;
	}
	else
	{
		ArcNode *p = G.vertices[x].first;//指向图G的顶点x的邻接点的指针
		int i = p->adjvex;//邻接点的序号
		return i;
	}

}

//假设图G中顶点y是顶点x的一个邻接点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1
int NextNeighbor(ALGraph G,int x,int y)
{
	ArcNode *p = G.vertices[x].first;
	while(p->adjvex != y)
	{
		p = p->next;
	}
	if(p->next == NULL)
	{
		return -1;
	}
	else
	{
		p = p->next;
		int j = p->adjvex;
		return j;
	}
}


//队列的函数

//1.初始化
void InitQueue(LinkQueue &Q)
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	Q.rear->next = NULL;
}

//2.入队
void EnQueue(LinkQueue &Q, int x)
{
  LinkNode *p = (LinkNode*)malloc(sizeof(LinkNode));
  if(p == NULL)
  {
    printf("动态内存分配失败！");
	exit(-1);
  }
  p->data = x;
  //通过尾插法入队
  p->next = NULL;
  Q.rear->next = p;
  Q.rear = p;
}

//3.出队
int DeQueue(LinkQueue &Q,int &x)
{
  if(IsEmpty(Q))
	  return -1;
  else
  {
	  LinkNode *p = Q.front->next;
	  x = p->data;
	  Q.front->next = p->next;
	  if(Q.rear == p)
		  Q.rear = Q.front;
	  free(p);
  }
  return x;
}

//4.判断空
bool IsEmpty(LinkQueue Q)
{
	if(Q.front == Q.rear)
	{
	  return true;
	}
	else
	{
	  return false;
	}
}


//广度优先遍历
//1.对图G进行广度优先遍历
void BFSTraverse(ALGraph G)
{
	int *visited = (int *)malloc(sizeof(int)*G.vexnum);
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;//标记数组，等于0表示顶点还未被访问
	}
	for(int i = 0; i < G.vexnum; ++i)
	{
	  if(visited[i] == 0)
	     BFS(G,visited,i);
	}
	printf("\n");
}

//2.广度优先遍历
void BFS(ALGraph G, int *visited, int v)
{
	printf("%c ",G.vertices[v].data);
	visited[v] = 1;//改成1表示该顶点已经被访问
	LinkQueue Q;//定义队列变量
	InitQueue(Q);//初始化队列
	EnQueue(Q,v);//入队
	while(!IsEmpty(Q))
	{
	  DeQueue(Q,v);//出队
	  for(int w = FirstNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w))
	  {
	    if(visited[w] == 0)
		{
			printf("%c ",G.vertices[w].data);//将第一个邻接点打印输出
			visited[w] = 1;//将该顶点标记为已经访问
			EnQueue(Q,w);//将顶点入队
		}
	  }
	}
}


//1.对图G进行深度优先遍历
void DFSTraverse(ALGraph G)
{
  	int *visited = (int *)malloc(sizeof(int)*G.vexnum);
	for(int i = 0; i < G.vexnum; ++i)
	{
	  visited[i] = 0;//标记数组，等于0表示顶点还未被访问
	}
	for(int i = 0; i < G.vexnum; ++i)
	{
      if(visited[i] == 0)
	     DFS(G,visited,i);
	}
	printf("\n");
}

//2.深度优先遍历
void DFS(ALGraph G, int *visited, int v)
{
	printf("%c ",G.vertices[v].data);
	visited[v] = 1;
	for(int w = FirstNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w))
	{
		if(visited[w] == 0)
		{
			visited[w] = 1;
			DFS(G,visited,w);//进行递归
		}
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/692164.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MyBatis 从初识到掌握

MyBatis 从初识到掌握

目录 今日良言&#xff1a;与其抱怨于黑暗&#xff0c;不如提灯向前行 一、初识MyBatis 1.MyBatis定义 2.为什么要学习MyBatis 3.MyBatis的创建 二、MyBatis的相关操作 1.增删改查操作 2.动态SQL使用 今日良言&#xff1a;与其抱怨于黑暗&#xff0c;不如提灯向前行 一…
阅读更多...
UE4/5 通过Control rig的FullBody【蜘蛛模型，不用basic ik】

UE4/5 通过Control rig的FullBody【蜘蛛模型，不用basic ik】

目录 根设置 FullBody IK 额外骨设置 ​编辑 晃动效果 根设置 第一步你需要准备一个蜘蛛模型&#xff0c;不论是官方示例或者是epic上购买的模型 然后我用的是epic上面购买的一个眼球蜘蛛&#xff1a; 第一步&#xff0c;我们从根创建一个空项【这个记得脱离父子级到root之…
阅读更多...
SQLServer 2016 R2数据库新建、附加、分离、备份、还原、复制等基本操作

SQLServer 2016 R2数据库新建、附加、分离、备份、还原、复制等基本操作

一、打开Microsoft SQL Server Management Studio 在桌面上找到图标&#xff0c;双击运行 打开Microsoft SQL Server Management Studio 17 输入服务器名称&#xff0c;选择SQL Server 身份验证&#xff0c;sa和sa密码&#xff0c;可以勾选记住密码&#xff0c;以便以后的登录…
阅读更多...
分享基于安卓项目的单元测试总结

分享基于安卓项目的单元测试总结

前言&#xff1a; 负责公司的单元测试体系的搭建&#xff0c;大约有一两个月的时间了&#xff0c;从最初的框架的调研&#xff0c;到中期全员的培训&#xff0c;以及后期对几十个项目单元测试的引入和推进&#xff0c;也算是对安卓的单元测试有了一些初步的收获以及一些新的认…
阅读更多...
【雕爷学编程】Arduino动手做（131）---跑马灯矩阵键盘模块

【雕爷学编程】Arduino动手做（131）---跑马灯矩阵键盘模块

37款传感器与执行器的提法&#xff0c;在网络上广泛流传&#xff0c;其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块&#xff0c;依照实践出真知&#xff08;一定要动手做&#xff09;的理念&#xff0c;以学习和交流为目的&am…
阅读更多...
线性代数基础--矩阵

线性代数基础--矩阵

矩阵 矩阵是由排列在矩形阵列中的数字或其他数学对象组成的表格结构。它由行和列组成&#xff0c;并且在数学和应用领域中广泛使用。 基本概念 元素&#xff1a;矩阵中的每个数字称为元素。元素可以是实数、复数或其他数学对象。 维度&#xff1a;矩阵的维度表示矩阵的行数和…
阅读更多...
vtk创建点

vtk创建点

使用vtk库创建三维空间中的点 引言开发环境示例一项目结构实现代码 运行效果示例二项目结构实现代码 运行效果总结 引言 本文仅适合初学者。 本文不提供vtk动态库的生成&#xff0c;以及在QtCreator中的引进vtk时的配置。 本文先由示例一开始&#xff0c;然后再在示例一的基础…
阅读更多...
aws使用外部 ID对其他账号授权

aws使用外部 ID对其他账号授权

点击前往授权,进入控制台 https://signin.aws.amazon.com/signin?redirect_urihttps%3A%2F%2Fconsole.aws.amazon.com%2Fconsole%2Fhome%3FhashArgs%3D%2523%26isauthcode%3Dtrue%26state%3DhashArgsFromTB_eu-north-1_f2d9c316b93c0026&client_idarn%3Aaws%3Asignin%3A%…
阅读更多...
Glassdoor美国公司员工及面试者评价数据

Glassdoor美国公司员工及面试者评价数据

一、数据简介 除了股东、债权人、政府等外部利益相关者外&#xff0c;员工的利益更应该得到公司的恰当保护&#xff0c;因为员工才是公司创造价值的真正主体。提高企业在产品市场的竞争力&#xff0c;首先就是要提高员工对企业的满意度&#xff0c;只有员工的满意度更高、幸福感…
阅读更多...
7个技巧，助你同时轻松管理和跟踪多个项目

7个技巧，助你同时轻松管理和跟踪多个项目

仅仅想到要兼顾这么多重要的职责&#xff0c;就会让许多专业的项目经理感到焦虑。当涉及多个项目的多种项目管理工具的处理&#xff0c;即使对于了解项目管理的项目经理来说&#xff0c;也是一项艰巨的任务&#xff0c;而对于在这个领域没有经过适当培训的人来说&#xff0c;这…
阅读更多...
强化学习从基础到进阶--案例与实践[7.1]：深度确定性策略梯度DDPG算法、双延迟深度确定性策略梯度TD3算法详解项目实战

强化学习从基础到进阶--案例与实践[7.1]：深度确定性策略梯度DDPG算法、双延迟深度确定性策略梯度TD3算法详解项目实战

【强化学习原理项目专栏】必看系列&#xff1a;单智能体、多智能体算法原理项目实战、相关技巧&#xff08;调参、画图等、趣味项目实现、学术应用项目实现 专栏详细介绍&#xff1a;【强化学习原理项目专栏】必看系列&#xff1a;单智能体、多智能体算法原理项目实战、相关技巧…
阅读更多...
计算机网络—数据链路层

计算机网络—数据链路层

文章目录 数据链路层服务差错编码多路访问协议信道划分随机访问MAC协议 数据链路层服务 该层中的帧数据结构&#xff1a; 帧头部会因为不同的局域网协议而不同&#xff0c;因此会在另一篇博文中继续介绍不同的帧数据报&#xff0c;不在本博文介绍。&#xff08;不过除了PPP协…
阅读更多...
Docker学习笔记11

Docker学习笔记11

Docker容器镜像&#xff1a; 1&#xff09;docker client 向docker daemon发起创建容器的请求&#xff1b; 2&#xff09;docker daemon查找本地有客户端需要的镜像&#xff1b; 3&#xff09;如无&#xff0c;docker daemon则到容器的镜像仓库中下载客户端需要的镜像&#…
阅读更多...
线性代数基础--向量

线性代数基础--向量

目录 向量的概念 基本概念 抽象概念 向量的意义 几何意义 物理意义 欧式空间 特点和性质 行向量与列向量 行向量 列向量 两者的关系 向量的基本运算与范数 向量的基本运算 向量的加法 数乘运算&#xff08;实数与向量相乘&#xff09; 转置 向量的范数 向量…
阅读更多...
echart 设置柱状图y轴最大刻度

echart 设置柱状图y轴最大刻度

start 最近接到需求希望柱状图 y轴最大高度可以略高一些&#xff1b;柱状图的数据能展示在柱状图的上方 记录一下相关配置项 解决方案 官方文档说明 https://echarts.apache.org/zh/option.html#xAxis.max 效果 代码 {key: business,title: {text: 业务领域分类,textSt…
阅读更多...
DAY32：回溯算法（七）全排列+全排列Ⅱ（排列问题）

DAY32：回溯算法（七）全排列+全排列Ⅱ（排列问题）

文章目录 46.全排列思路树形图used数组的作用 伪代码完整版时间复杂度总结 47.全排列Ⅱ思路树形图 完整版时间复杂度总结 46.全排列 给定一个不含重复数字的数组 nums &#xff0c;返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1&#xff1a; 输入&#xf…
阅读更多...
C#和LABVIEW的对决：哪种上位机编程语言更适合你？

C#和LABVIEW的对决：哪种上位机编程语言更适合你？

今天&#xff0c;我们将谈论主流的上位机编程语言。你听说过C#和LABVIEW吗&#xff1f;它们是的上位机编程语言&#xff0c;C#作为自动化主流编程语言特别受欢迎&#xff0c;LABVIEW用于自动化测试&#xff0c; 首先&#xff0c;我们来了解C#语言。C#是一种文本语言&#xff0c…
阅读更多...
2023年江西省研究生数模竞赛植物的多样性

2023年江西省研究生数模竞赛植物的多样性

2023年江西省研究生数模竞赛 植物的多样性 原题再现 植物作为食物链中的生产者&#xff0c;通过光合作用吸收二氧化碳&#xff0c;制造氧气&#xff0c;同时为其他生物提供食物和栖息地&#xff0c;支持它们的生存。植物在生态系统中还起到防止水土流失、缓解温室效应等作用。…
阅读更多...
新手小白编程利器！Debug 断点调试工具IDEA

新手小白编程利器！Debug 断点调试工具IDEA

前言 很多新手小白在学习的时候总会遇到一个问题&#xff1a; 我们一运行程序&#xff0c;只能看到程序最后的结果&#xff0c;但是这个程序究竟是怎么一步步运行出这样的结果呢&#xff1f;如果有一个工具能够让我们看到我们程序的执行流程该有多好~ 这就需要用到新手小白编程…
阅读更多...
modbus转MQTT网关支持自定义JSON格式

modbus转MQTT网关支持自定义JSON格式

在工业自动化系统中&#xff0c;Modbus是一种非常常见的通信协议&#xff0c;而OPC UA则是近年来兴起的一种新型通信协议。由于各种设备之间使用的通信协议不尽相同&#xff0c;因此需要一种能够实现多种协议转换的网关产品。BL110网关就是一款能够实现Modbus到OPC UA转换的产品…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023