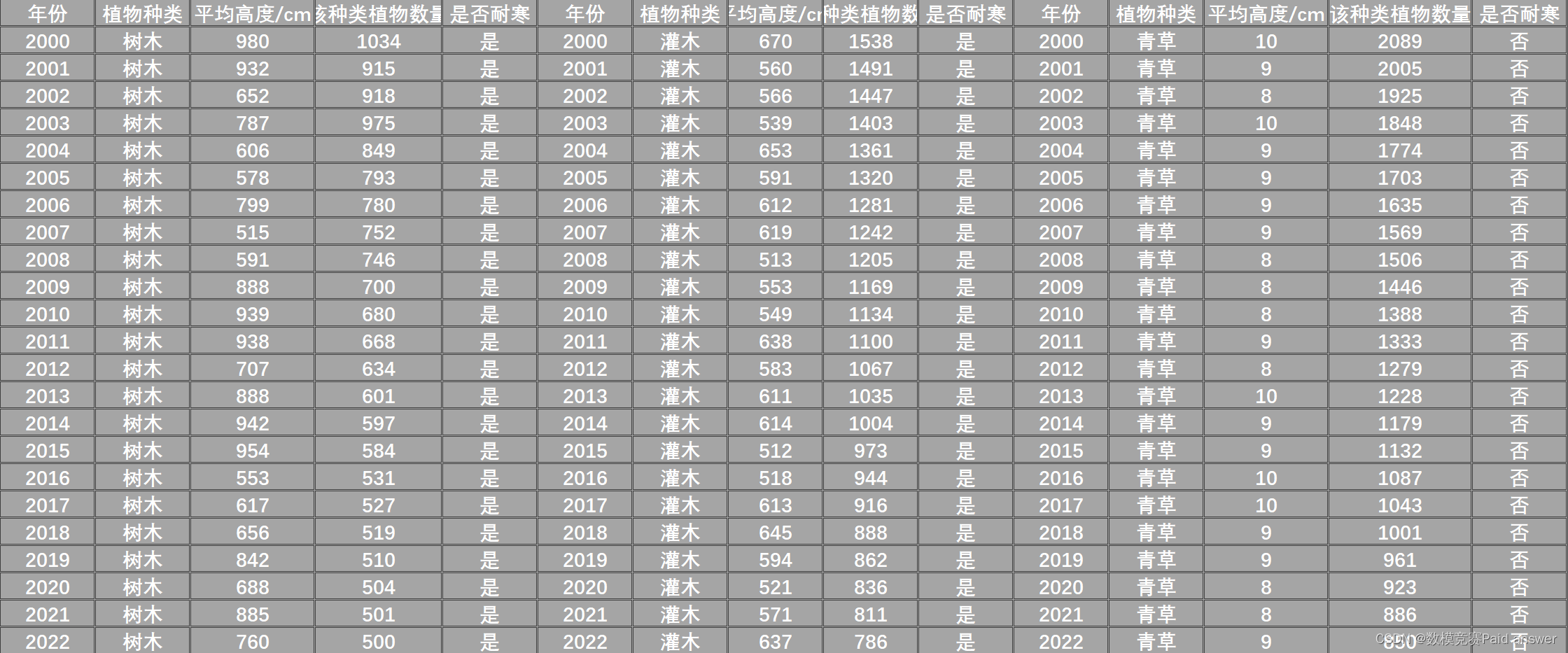
46.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

思路

本题的nums中没有重复元素，因此求集合不需要去重的操作。

本题是排列，排列是强调元素顺序的！之前的题目基本都可以归类为组合问题，组合并不强调元素顺序。

在排列问题中，我们需要用used数组来标记使用过的元素，避免重复取到同一个元素，和组合里的startIndex不同，此时是不需要startIndex的，因为遍历到后面还是需要从0开始。

但是我们需要标记已经取过的元素，来看后面的元素取什么，所以需要used数组标记已经选择过的元素！

树形图

通过树形图很容易发现，排列和组合问题的区别是，排列是记录当前遍历过的元素，然后这个分支没遍历过的元素，也就是used对应下标0的元素，都需要再遍历一遍！

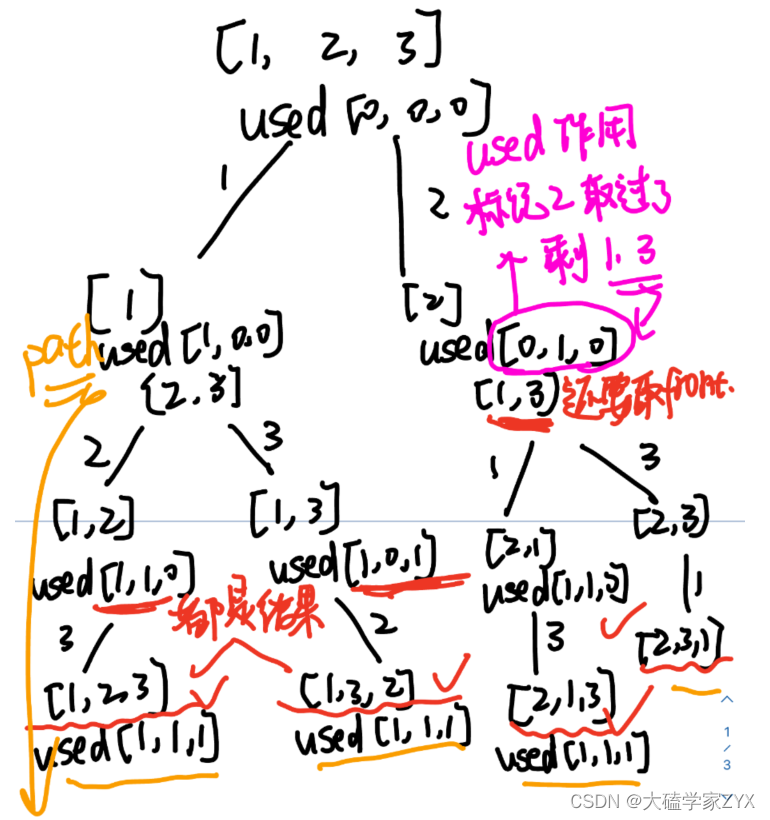
used数组的作用

排列问题中的used数组，实际上就是看这个分支取过了哪些元素，只要取过的元素别重复取就可以了，前面的元素这个分支没遍历，还是要继续遍历。

伪代码

• 每个分支都要传入used

void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>&nums,vector<int>&used){
    //终止条件：收集的path大小和nums大小相等
    if(path.size()==nums.size()){
        //叶子节点收集结果
        result.push_back(path);
        return;
    }
    
    //单层搜索,i从0开始，而不是startIndex，因为每次搜索都从头开始，不是used取过的就行
    for(int i=0;i<num.size();i++){
        //如果这个元素取过了，continue;
        if(used[i]==1){
            continue;
        }
        path.push_back(nums[i]);
        used[i] += 1;
        //递归
        backtracking(path,result,nums,used);
        //回溯
        used[i] -= 1;
        path.pop_back();
    }
    
}

完整版

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& nums,vector<int>&used){
        //终止条件
        if(path.size()==nums.size()){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=0;i<nums.size();i++){
            if(used[i]==1){
                continue;
            }
            path.push_back(nums[i]);
            used[i]+=1;
            //递归
            backtracking(path,result,nums,used);
            //回溯
            path.pop_back();
            used[i]-=1;
        }
        
    }
    vector<vector<int>> permute(vector<int>& nums) {
        //先定义一个和nums大小相等的下标计数数组
		vector<int>used(nums.size(),0);
        vector<int>path;
        vector<vector<int>>result;
        //传入函数
        backtracking(path,result,nums,used);
        return result;
        
    }
};

时间复杂度

本题的时间复杂度为O(n!)。

这个问题要求生成一个集合的所有可能排列，总共有**n!**个排列，其中n是数组的大小。在这个问题中，解决方案是通过回溯法，对数组中的每一个元素，进行选择或不选择的操作，进行深度优先遍历，直到遍历完所有可能的路径。

对于空间复杂度，由于需要存储所有的排列，最坏的情况是需要存储n!个排列，因此空间复杂度也是O(n!)。

总结

排列问题的不同：

• for循环遍历，每次都是从0开始
• 终止条件是path的大小和原数组相同才停下
• 需要used数组在每个分支path里面,记录这个分支遍历了多少数字，每个分支path里所有数字都要遍历一遍

47.全排列Ⅱ

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

思路

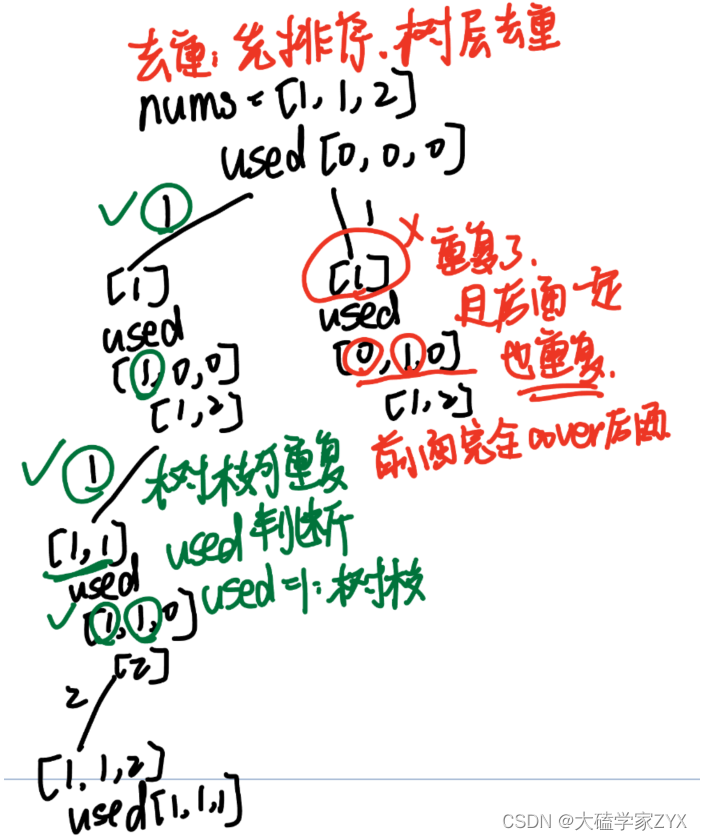
因为本题给出的是包含重复数字的序列 nums，因此涉及到去重的问题。

树形图

本题的去重逻辑和之前用排序+used数组的逻辑是一样的。也是树层去重，树枝不去重。

完整版

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& nums,vector<int>&used){
        //终止条件
        if(path.size()==nums.size()){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=0;i<nums.size();i++){
            //是否重复，重复跳过
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==0){
                continue;
            }
            //这个数字在当前分支遍历过了，也跳过
            if(used[i]!=0){
                continue;
            }
            path.push_back(nums[i]);
            used[i] += 1;
            //递归
            backtracking(path,result,nums,used);
            //回溯
            path.pop_back();
            used[i] -= 1;
        }
        
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        //定义used并初始化
        vector<int>used(nums.size(),0);
        //排序
        sort(nums.begin(),nums.end());
        
        vector<int>path;
        vector<vector<int>>result;
        backtracking(path,result,nums,used);
        
        return result;
    }
};

时间复杂度

本题的时间复杂度也是O(n!)。

这个问题是要生成一个包含重复元素的集合的所有可能排列，并且要避免重复的排列。本题解决方案是先对数组进行排序，然后使用一个标记数组used来跳过重复的元素。

虽然在这个问题中有重复的元素，但实际上并没有减少需要遍历的排列的数量。所以，时间复杂度仍然是O(n!)。空间复杂度也是O(n!)，和全排列一样。

总结

涉及到去重的回溯问题，一定要画树形图标出used，树形图画出来了逻辑就清楚了。