题意：

 

D. 光学实验

时间限制：5秒

内存限制：256兆字节

输入：标准输入

输出：标准输出

Phunsuk Wangdu教授进行了一些关于光线的实验。n条光线的实验装置如下：

有一个长方形盒子，在相对的两面上有恰好n个孔。所有光线从第一面的孔进入，从盒子的另一面的孔出射。每个孔只能进入或出射一条光线。这些孔位于一条直线上。

Wangdu教授正在向学生展示他的实验。他展示了这样的情况：有些光线的组合，其中每一条光线与组合中的其他光线都相交。一个好奇的学生问教授：“老师，是否存在一些光线的组合，其中所有光线都与组合中的每一条光线相交？我们能够确定这种组合中光线的最大数量吗？"

Wangdu教授陷入了困境，因为他知道你很聪明，所以他请你帮助他。

输入

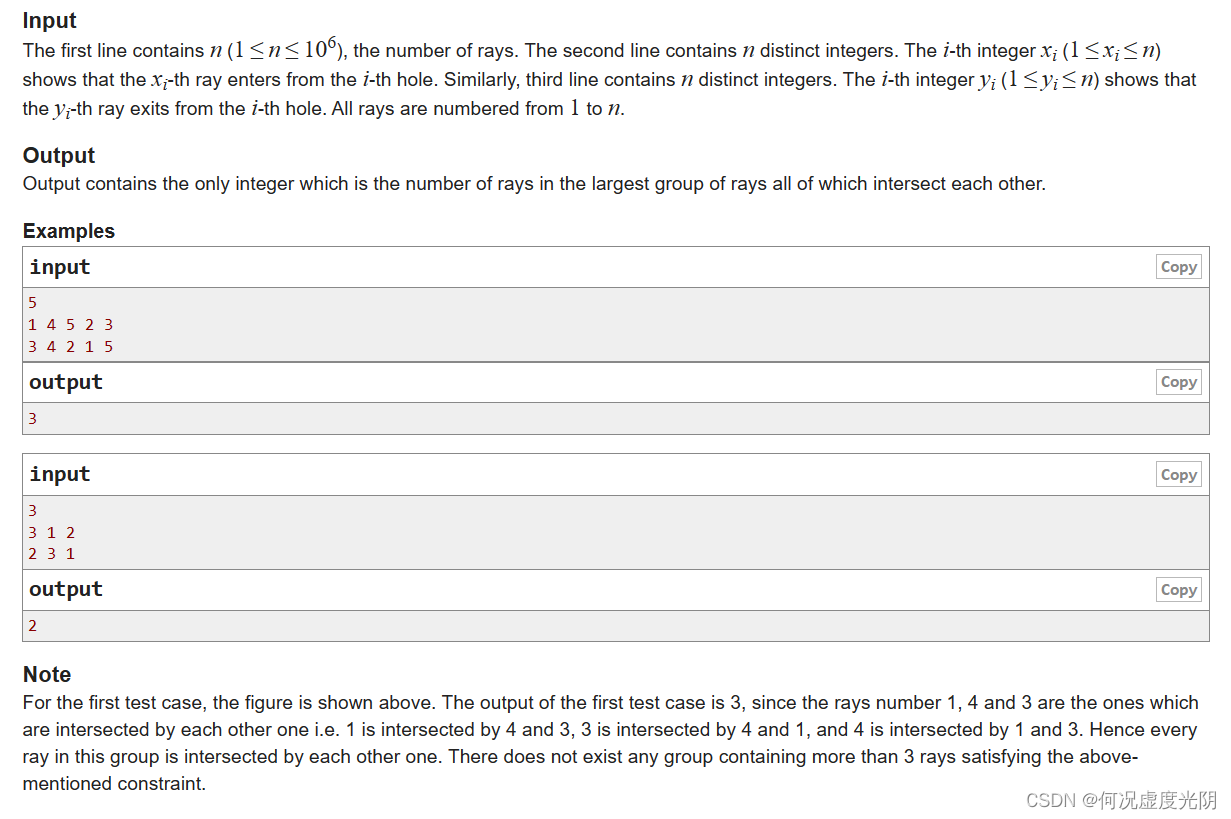
第一行包含一个整数n（1 ≤ n ≤ 106），表示光线的数量。第二行包含n个不同的整数。第i个整数xi（1 ≤ xi ≤ n）表示第i条光线从第i个孔进入。类似地，第三行包含n个不同的整数。第i个整数yi（1 ≤ yi ≤ n）表示第i条光线从第i个孔出射。所有光线从1到n编号。

输出

输出包含一个整数，表示光线中最大的相互相交的组合中光线的数量。

示例
输入
5
1 4 5 2 3
3 4 2 1 5
输出
3
输入
3
3 1 2
2 3 1
输出
2
注意
对于第一个测试用例，上述图中所示。第一个测试用例的输出是3，因为光线1、4和3是彼此相交的光线，即1与4和3相交，3与4和1相交，4与1和3相交。因此，该组合中的每条光线都与其他光线相交。不存在满足上述条件的包含超过3条光线的组合。

思路：

所选光线按射入洞口编号排序后，其射出洞口编号必然倒序，故对所有光线按射入洞口编号排序后对其射出洞口编号求一个LIS即可

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
const int INF=2e18;
int a[N],dp[N];
int n;
int LIS()
{
    for(int i=1;i<n;i++)dp[i]=INF;
    dp[0]=a[0];
    int len=1;
    for(int i=1;i<n;i++)
        if(a[i]>dp[len-1])dp[len++]=a[i];
        else dp[lower_bound(dp,dp+n,a[i])-dp]=a[i]; 
    return len;
}
pair<int,int>f[N];
void solve(){
	cin>>n;
	for(int i=0;i<n;i++){
		int x;
		cin>>x;
		a[x-1]=i;
	}
	for(int i=0;i<n;i++){
		f[i].first=a[i];
	}
	for(int i=0;i<n;i++){
		int x;
		cin>>x;
		a[x-1]=i;
	}
	for(int i=0;i<n;i++) f[i].second=a[i];
	sort(f,f+n);
	for(int i=0;i<n;i++){
		a[i]=f[n-i-1].second;
	}
	cout<<LIS()<<"\n";
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	int t=1;
	while(t--){
		solve();
	}
}