1.逻辑回归(Logistics Regression)的原理及实现
笔记来源于《白话机器学习的数学》
逻辑回归用于解决二分类问题
1.1 逻辑回归的原理
1.1.1 Sigmoid函数
sigmoid函数在神经网络中如何起作用?详见本人笔记:机器学习和AI底层逻辑
复杂非线性分类->多个线段->每个线段是叠加而来的->sigmoid函数作为小线段的来源->不同的sigmoid可以叠加成任意形状的小线段,多个小线段拼接得到最终复杂分类的线段->这个过程用抽象的方法表达(神经网络)
sigmoid函数将数据 x \boldsymbol{x} x映射到 [ 0 , 1 ] [0,1] [0,1],概率范围刚好也是 [ 0 , 1 ] [0,1] [0,1],可以用概率大小与阈值比较来判断数据属于哪个类别

x
\boldsymbol{x}
x为数据、y为标签(表示哪个分类)、
θ
\boldsymbol{\theta}
θ为未知参数向量(先假设一个初始向量随后通过训练得到最优结果)、
θ
T
x
\boldsymbol{\theta}^{T}\boldsymbol{x}
θTx为分类边界、
若数据线性可分的则分类边界为直线
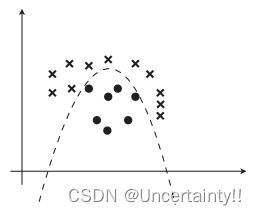
若数据线性不可分则分类边界为曲线
若
θ
T
x
<
0
\boldsymbol{\theta}^{T}\boldsymbol{x}\lt 0
θTx<0,则
f
θ
(
x
)
<
0.5
f_{\boldsymbol{\theta}}(\boldsymbol{x})\lt0.5
fθ(x)<0.5,
f
θ
(
x
)
=
P
(
y
=
0
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=0|\boldsymbol{x})
fθ(x)=P(y=0∣x)(数据属于分类0的概率),概率在
[
0
,
0.5
]
[0,0.5]
[0,0.5]范围,则数据判别为属于分类0
若
θ
T
x
>
0
\boldsymbol{\theta}^{T}\boldsymbol{x}\gt 0
θTx>0,则
f
θ
(
x
)
>
0.5
f_{\boldsymbol{\theta}}(\boldsymbol{x})\gt0.5
fθ(x)>0.5,
f
θ
(
x
)
=
P
(
y
=
1
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=1|\boldsymbol{x})
fθ(x)=P(y=1∣x)(数据属于分类1的概率),概率在
[
0.5
,
1
]
[0.5,1]
[0.5,1]范围,则数据判别为属于分类1

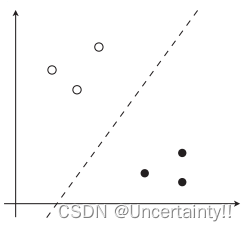
| 
|

通过训练调整参数达到最优结果
1.1.2 似然函数
对于二分类的情况,标签y的取值只有0、1,满足
P
(
y
=
0
∣
x
)
+
P
(
y
=
1
∣
x
)
=
1
P(y=0|\boldsymbol{x})+P(y=1|\boldsymbol{x})=1
P(y=0∣x)+P(y=1∣x)=1
数据与标签的理想关系
标签
y
=
0
y=0
y=0 时,我们希望数据为标签0的概率
f
θ
(
x
)
=
P
(
y
=
0
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=0|\boldsymbol{x})
fθ(x)=P(y=0∣x)最大
标签
y
=
1
y=1
y=1 时,我们希望数据为标签1的概率
f
θ
(
x
)
=
P
(
y
=
1
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=1|\boldsymbol{x})
fθ(x)=P(y=1∣x)最大
所有训练数据中的每个数据取到正确标签的概率乘积起来就是所有数据取到正确标签的概率(联合概率),即逻辑回归的目标函数/代价函数:似然函数
最大化似然估计求似然函数的极大值,进而得到参数估计值,求代价函数的最小值就是对似然函数的极大化
下面我们求似然函数的最大值

首先对似然函数取对数,由于对数函数也是单增函数,我要求最大化似然函数,所有取对数后不影响似然函数的增减性

对上述结果进行微分

∂
u
∂
θ
j
=
∑
i
=
1
n
(
y
(
i
)
−
f
θ
(
x
(
i
)
)
)
x
j
(
i
)
\frac{\partial u}{\partial \theta_j}=\sum_{i=1}^{n}\big(y^{(i)}-f_{\theta}(\boldsymbol{x}^{(i)})\big)x_j^{(i)}
∂θj∂u=i=1∑n(y(i)−fθ(x(i)))xj(i)
采用梯度下降法迭代参数,最终获得最优参数
参数的更新表达式

若想要与普通回归的参数更新表达式统一,则将括号内提出负号,将负号写到学习率前

1.3 逻辑回归的实现
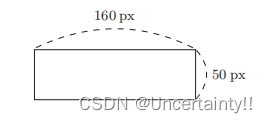
输入图像水平方向和竖直方向的像素,判断该图像是纵向的还是横向的?
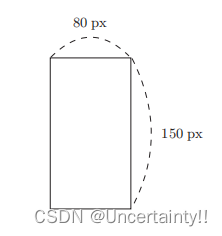
| 
|
1.3.1 线性可分的数据
x
1
x1
x1为水平方向像素、
x
2
x2
x2为竖直方向像素、
y
y
y为标签,
y
=
0
y=0
y=0代表该图像为纵向的,
y
=
1
y=1
y=1代表该图像为横向的

import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('~/Downloads/sourcecode-cn/images2.csv', delimiter=',', skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]
# 参数初始化
theta = np.random.rand(3)
# 标准化
mu = train_x.mean(axis=0)
sigma = train_x.std(axis=0)
对变量进行标准化,求出变量x所有数值的均值和标准差,利用下式对所有数值进行标准化
def standardize(x):
return (x - mu) / sigma
train_z = standardize(train_x)
# 增加 x0
def to_matrix(x):
x0 = np.ones([x.shape[0], 1])
return np.hstack([x0, x])
X = to_matrix(train_z)
将标准化的训练数据绘图
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.show()
线性可分类数据

# sigmoid 函数
def f(x):
return 1 / (1 + np.exp(-np.dot(x, theta)))

# 分类函数
def classify(x):
return (f(x) >= 0.5).astype(np.int) # 将概率大于0.5的直接处理为1
# 学习率
ETA = 1e-3
# 重复次数
epoch = 5000
# 更新次数
count = 0
我们把重复次数 epoch 设置得稍微多一点,比如 5000 次左右。在实际问题中需要通过反复尝试来设置这个值,即通过确认学习中的精度来确定重复多少次才足够好
# 重复学习
for _ in range(epoch):
theta = theta - ETA * np.dot(f(X) - train_y, X)
# 日志输出
count += 1
print('第 {} 次 : theta = {}'.format(count, theta))
下式为参数更新表达式,上述循环体中的表达式为下式的矩阵形式

上面循环体中参数更新表达式使用矩阵进行更新,具体的公式推导详见本人博客:多项式回归的原理及实现、多重回归的原理
学习完成后得到参数的最优结果,将这些参数的最优结果代入分类边界表达式

# 绘图确认
x0 = np.linspace(-2, 2, 100)
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.plot(x0, -(theta[0] + theta[1] * x0) / theta[2], linestyle='dashed')
plt.show()

使用Sigmoid函数验证预测结果
f返回x的横向概率

图像1为横向的概率为91.7%,图像2为横向的概率为2.9%
使用分类函数验证预测结果

图像1为类别1即横向图像,图像2为类别2即纵向图像
1.3.1 线性不可分的数据
x
1
x1
x1为水平方向像素、
x
2
x2
x2为竖直方向像素、
y
y
y为标签,
y
=
0
y=0
y=0代表该图像为纵向的,
y
=
1
y=1
y=1代表该图像为横向的

import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('~/Downloads/sourcecode-cn/data3.csv', delimiter=',', skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]
# 参数初始化
theta = np.random.rand(4)
# 标准化
mu = train_x.mean(axis=0)
sigma = train_x.std(axis=0)
def standardize(x):
return (x - mu) / sigma
train_z = standardize(train_x)
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.show()

# 增加 x0 和 x3
def to_matrix(x):
x0 = np.ones([x.shape[0], 1])
x3 = x[:,0,np.newaxis] ** 2
return np.hstack([x0, x, x3])
X = to_matrix(train_z)

决策边界表达式

# sigmoid 函数
def f(x):
return 1 / (1 + np.exp(-np.dot(x, theta)))
# 分类函数
def classify(x):
return (f(x) >= 0.5).astype(np.int)
# 学习率
ETA = 1e-3
# 重复次数
epoch = 5000
# 更新次数
count = 0
我们把重复次数 epoch 设置得稍微多一点,比如 5000 次左右。在实际问题中需要通过反复尝试来设置这个值,即通过确认学习中的精度来确定重复多少次才足够好
# 重复学习
for _ in range(epoch):
theta = theta - ETA * np.dot(f(X) - train_y, X)
# 日志输出
count += 1
print('第 {} 次 : theta = {}'.format(count, theta))
下式为参数更新表达式,上述循环体中的表达式为下式的矩阵形式

上面循环体中参数更新表达式使用矩阵进行更新,具体的公式推导详见本人博客:多项式回归的原理及实现、多重回归的原理
迭代结果

学习完成后得到参数的最优结果,将这些参数的最优结果代入分类边界表达式

# 绘图确认
x1 = np.linspace(-2, 2, 100)
x2 = -(theta[0] + theta[1] * x1 + theta[3] * x1 ** 2) / theta[2]
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.plot(x1, x2, linestyle='dashed')
plt.show()
x
1
x1
x1为横轴、
x
2
x2
x2为纵轴

验证一下模型,以迭代次数为横轴,精度为纵轴绘图
# 参数初始化
theta = np.random.rand(4)
# 精度的历史记录
accuracies = []
# 重复学习
for _ in range(epoch):
theta = theta - ETA * np.dot(f(X) - train_y, X)
# 计算现在的精度
result = classify(X) == train_y
accuracy = len(result[result == True]) / len(result) # 模型评估指标:精度
accuracies.append(accuracy)

# 将精度绘图
x = np.arange(len(accuracies))
plt.plot(x, accuracies)
plt.show()
观察下图,随着迭代次数的增加,精度越来越逼近1,迭代次数在900次时,精度基本达到1,所以迭代次数 epoch 可以设置为1000左右

上述过程中使用梯度下降法(使用所有训练数据)对目标函数进行优化
若使用随机梯度下降法(使用一个训练数据)对目标函数进行优化
只修改学习部分中循环体部分即可
# 重复学习
for _ in range(epoch):
p = np.random.permutation(X.shape[0])
for x, y in zip(X[p,:], train_y[p]):
theta = theta - ETA * (f(x) - y) * x