文章目录
- 迷宫最短路径和输出
- 深度优先
- 广度优先
- 48 旋转矩阵图像
- 大数加减法
- 146 LRU 缓存算法
- 460 LFU 缓存算法
迷宫最短路径和输出
给定一个 n × m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1 ,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1, 1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 ( n, m ) 处,至少需要移动多少次。
数据保证 (1, 1) 处和 ( n, m ) 处的数字为 0 ,且一定至少存在一条通路。
Input
第一行包含两个整数 n 和 m 。1 ≤ n, m ≤ 100
接下来 n 行,每行包含 m 个整数( 0 或 1 ),表示完整的二维数组迷宫。
Output
输出一个整数,表示从左上角移动至右下角的最少移动次数以及移动路径。
Sample Input
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
8
1 1
2 1
3 1
3 2
3 3
3 4
3 5
4 5
5 5
深度优先
#include<iostream>
#include<vector>
using namespace std;
vector<pair<int, int>> path; //当前搜索到的路径
vector<pair<int, int>> res; //记录的最短的路径
int minLength = INT_MAX;
void dfs(vector<vector<int>>& grid, int x, int y, int step) {
if (x == grid.size() - 1 && y == grid[0].size() - 1) { //搜索到目的地点
if (res.size() == 0 || res.size() > path.size()) res = path;
if (step < minLength) minLength = step;
return;
}
int dx[4] = {0, 1, 0, -1}; //右下左上
int dy[4] = {1, 0, -1, 0};
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx < 0 || nx >= grid.size() || ny < 0 || ny >= grid[0].size() || grid[nx][ny] != 0) continue;// 边界判定一定要在前面!!!
grid[nx][ny] += 5; //将迷宫路径置为其他值 不走重复路 未设置原先的grid[x][y]但是不受影响 在下一个坐标会把x、y覆盖
path.push_back({nx, ny});
dfs(grid, nx, ny, step + 1); //小循环
path.pop_back();
grid[nx][ny] -= 5; //恢复现场 因为有可能其他路与之前的路径会有重叠路径 若不恢复现场 则此次走过的路 在下一个大小循环中不能再走
}
}
int main() {
int row, col;
cin >> row >> col;
vector<vector<int>> grid(row, vector<int> (col));
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cin >> grid[i][j];
}
}
dfs(grid, 0, 0, 0); // 大循环
cout << "minLength is " << minLength << endl;
for (int i = 0; i < res.size(); i++) {
cout << res[i].first << " " << res[i].second << endl;
}
system("pause");
return 0;
}
广度优先
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int minLength = 0;
void print(int x,int y, vector<vector<int>>& fax, vector<vector<int>>& fay){
if(x==0 && y==0){
cout << "(" << x << ", " << y << ")" <<endl;
return;
}
print(fax[x][y], fay[x][y], fax, fay); // 从最后一个坐标递归回溯到前一个坐标
cout << "(" << x << ", " << y << ")" << endl;
}
void bfs(vector<vector<int>>& grid, vector<vector<int>>& visited, int x, int y, vector<vector<int>>& fax, vector<vector<int>>& fay) {
queue<pair<int, int>> q;
if (grid[x][y] != 0) return; // 判断起点是否合法
q.push(make_pair(x, y)); //队列q中存起点坐标x y
//bfs注意一定不能重复走!!!!
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
int row = q.front().first;
int col = q.front().second;
q.pop();
if (row == grid.size() - 1 && col == grid[0].size() - 1) {
print(grid.size() - 1, grid[0].size() - 1, fax, fay);
return; // 只要遍历到结果一定是最短路
}
for (int i = 0; i < 4; i++) {
int nx = row + dx[i];
int ny = col + dy[i];
if (nx < 0 || nx >= grid.size() || ny < 0 || ny >= grid[0].size() || grid[nx][ny] != 0 || visited[nx][ny] != 0) continue;
visited[nx][ny] = visited[row][col] + 1; // 走过的节点进行赋值 保证不走重复路 可用grid[nx][ny] = 1代替
q.push(make_pair(nx, ny));
fax[nx][ny] = row;
fay[nx][ny] = col;
}
}
minLength++; // 代表遍历的层数
}
}
int main() {
int row, col;
cin >> row >> col;
vector<vector<int>> grid(row, vector<int> (col));
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cin >> grid[i][j];
}
}
vector<vector<int>> visited(row, vector<int> (col, 0));
vector<vector<int>> fax(row, vector<int> (col, -1));
vector<vector<int>> fay(row, vector<int> (col, -1));
bfs(grid, visited, 0, 0, fax, fay);
cout << "minLength is " << minLength << endl; //或者visited[row - 1][col - 1]
cout << "------------------------------------" << endl;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cout << fax[i][j] << " ";
}
cout << endl;
}
cout << "------------------------------------" << endl;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cout << fay[i][j] << " ";
}
cout << endl;
}
system("pause");
return 0;
}
/*
求输出路径方法
开两个二维数组fax 和 fay 然后 分别记录上一个位置的x 和 y
*/
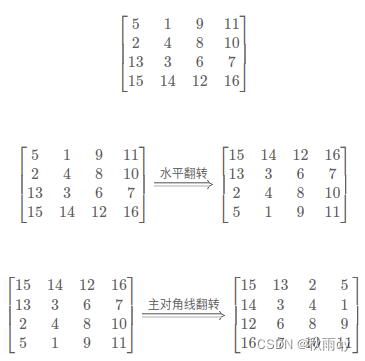
48 旋转矩阵图像
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
// 水平翻转
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < n; ++j) {
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
// 主对角线翻转
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
swap(matrix[i][j], matrix[j][i]);
}
}
}
};
大数加减法
参考链接:https://blog.csdn.net/mrqiuwen/article/details/127057549
因为较大整数的相加很可能超出整型的32位限制,或者本身就是超出限制的大数之间的加减运算。
所以需要单独写一个能大数相加减的函数。
基本原理:把数字用字符串的形式来保存加减的结果或大数字本身就不会超出限制,比如“999999999999999999999999999999” 多长都可以。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
class BigInt
{
public:
BigInt(string str) : strDigit(str){ }
private:
string strDigit;//使用字符串存储大整数
//都是全局函数声明为友元
friend ostream& operator<<(ostream& out, const BigInt& src);
friend BigInt operator+(const BigInt& lhs, const BigInt& rhs);
friend BigInt operator-(const BigInt& lhs, const BigInt& rhs);
};
//打印函数
ostream& operator<<(ostream& out, const BigInt& src)
{
out << src.strDigit;
return out;
}
//大数加法
BigInt operator+(const BigInt& lhs, const BigInt& rhs) {
//从后往前遍历字符串lhs,和rhs,用flag来标记是否需要进位,结果存在result数组中(反向的)
string result;
bool flag = false;
int i = lhs.strDigit.length() - 1;//string的length和size没有区别,length是沿用C语言习惯,早先只有length
int j = rhs.strDigit.length() - 1;
for (; i >= 0 && j >= 0; --i, --j) //i 和 j其中一个会被减到负数然后退出for循环
{
int ret = lhs.strDigit[i] - '0' + rhs.strDigit[j] - '0';//单个位加减时需要减'0'转成整型,每次都重新定义一个新的ret
if (flag)
{
ret += 1;//flag为true说明此位因为上一位进位而需要多加一个1
flag = false;//再将其重新置为false
}
//两个if不能互换,否则不是下一位进1
if (ret >= 10)
{
ret %= 10;
flag = true;
}
result.push_back(ret + '0');
}
//如果遍历完,i还有剩下,第一个字符串没完
if (i >= 0)//注意要取等,因为更短的那个字符串的下标是被减到-1,而不是0,0依然说明还剩余1位
{
while (i >= 0)
{
int ret = lhs.strDigit[i] - '0';
if (flag) //前面加过来可能还有进位,然后当前可能为9,加了1之后又 = 10,又得进位,所以直接复制前面的代码
{
ret += 1;
flag = false;
}
if (ret >= 10)
{
ret %= 10;
flag = true;
}
result.push_back(ret + '0');
i--;
}
}
//第二个字符串没完
else if (j >= 0)
{
while (j >= 0)
{
int ret = lhs.strDigit[j] - '0';
if (flag) //前面加过来可能还有进位,然后当前可能为9,加了1之后又 = 10,又得进位,所以直接复制前面的代码
{
ret += 1;
flag = false;
}
if (ret >= 10)
{
ret %= 10;
flag = true;
}
result.push_back(ret + '0');
j--;
}
}
//最高位可能也进位
if (flag) {
result.push_back('1');
}
reverse(result.begin(), result.end());
return result;//result是string类,而不是BigInt,因为隐式转换,p263
//因为编译器看到该类的构造函数只接受一个实参(而且是string类的),所以可以触发隐式转换机制,定义string result时编译器也会构建一个BigInt类的临时对象,并把result赋值给他
//函数里的return本来就是返回临时对象,这个时候就返回的就是那个BigInt类的临时对象
//当然,参考书上的例子,即使后面函数用string类的result,编译器实际传入的也是BigInt的临时对象
//如某成员函数定义为func(BigInt& a){...}; 调用时传入string类 func(result);也是合法的
}
//大数减法
BigInt operator-(const BigInt& lhs, const BigInt& rhs) {
//让大的减小的,如果lhs比rhs小,则让rhs - lhs,然后最后添加负号
string result;
bool flag = false;
bool minor = false;//标记lhs是否和rhs互换了
string maxStr = lhs.strDigit;
string minStr = rhs.strDigit;
if (maxStr.length() < minStr.length())
{
//互换,让maxStr一直是最长的
maxStr = rhs.strDigit;
minStr = lhs.strDigit;
minor = true;
}
//长度一样也得比较
else if (maxStr.length() == minStr.length())
{
if (maxStr < minStr)
{
maxStr = rhs.strDigit;//让maxStr是最大的
minStr = lhs.strDigit;
minor = true;
}
else if (maxStr == minStr)
{
return string("0");
}
}
int i = maxStr.length() - 1;//i肯定大于等于j,所以后面j会先完
int j = minStr.length() - 1;
for (; i >= 0 && j >= 0; --i, --j) {
int ret = maxStr[i] - minStr[j];//减法的话,char类型相减就是int型了,不用+‘0’再相减
/*if (ret >= 0)
{
result.push_back(ret + '0');
} 一定要先看标记,因为被借位的话,当前ret需要减1*/
if (flag)
{
ret -= 1;
flag = false;
}
//当前位有可能因为被借位了而减,小于0,所以紧接着判断是否为负
if (ret < 0)
{
ret += 10;// 如2 - 6,应该是12 - 6,所以为 2 - 6 + 10 = 6
flag = true;
}
result.push_back(ret + '0');
}
//肯定是j先完,所以不用再像加法那样判断,而是直接把i多余的处理完
while (i >= 0) {
int ret = maxStr[i] - '0';
if (flag) {
ret -= 1;
flag = false;
}
//同样的,ret可能原本是0,被借位了又为-1了
if (ret < 0) {
ret += 10;
flag = true;
}
result.push_back(ret + '0');
i--;
}
//翻转前先看看末尾有没有0,如1000,否则反转后就是0001
while(result.back() == '0')
{
result.pop_back();
}
if (minor) {
result.push_back('-');
}
reverse(result.begin(), result.end());
return result;
}
int main()
{
string s1;
string A;
string s2;
getline(cin, s1);
getline(cin, A);//把加减号定义为char会报错,getline第二个参数只能是string类型
getline(cin, s2);
BigInt int1(s1);
BigInt int2(s2);
if (A == "+") {
cout << int1 + int2 << endl;
}
if (A == "-") {
cout << int1 - int2 << endl;
}
return 0;
}
146 LRU 缓存算法
面筋:
今天面试的时候,面试官告诉我,put 函数里面要先写 if 判断 size 是否到达 cap,然后再添加数据。他的理由是内存可能就是没办法再新加一个元素。
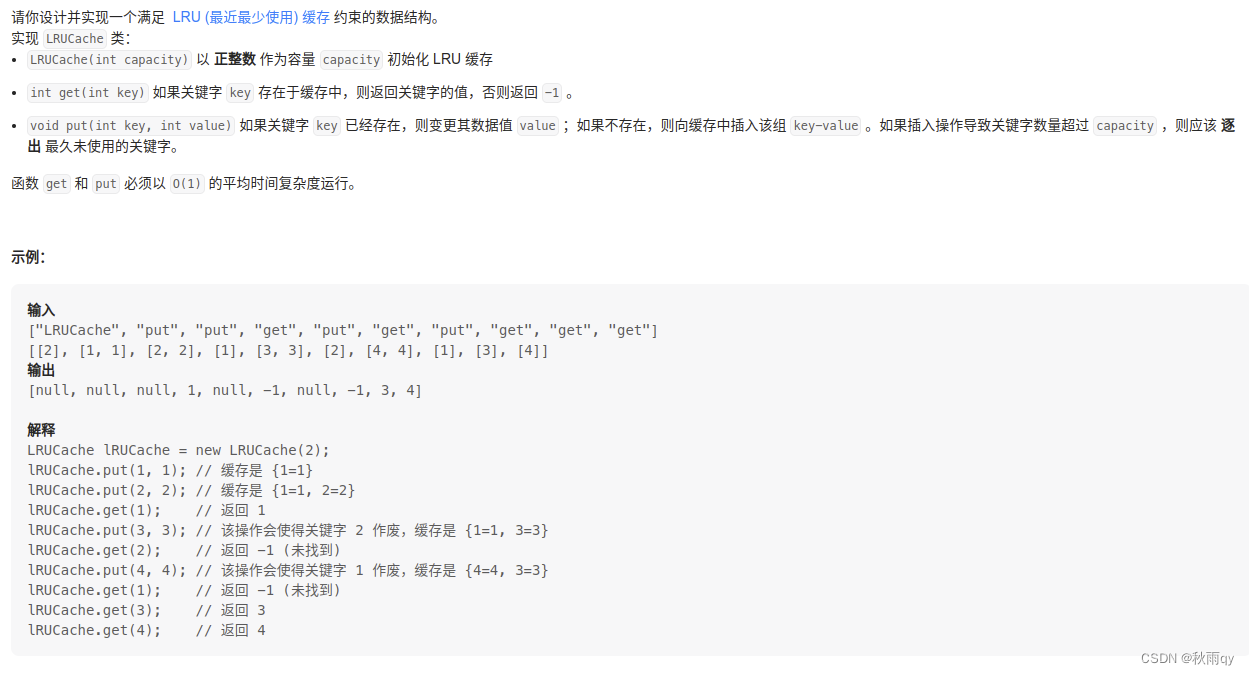
最近最少使用算法(Least Recently Used,LRU):一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段,用来记录一个页面自上次被访问以来所经历的时间 t,当须淘汰一个页面时,选择现有页面中其 t 值最大的,即最近最少使用的页面予以淘汰。
实现本题的两种操作,需要用到一个哈希表和一个双向链表。在面试中,面试官一般会期望我们能够自己实现一个简单的双向链表,而不是使用语言自带的、封装好的数据结构。
思路:用一个哈希表和一个双向链表维护所有在缓存中的键值对。
- 双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
- 哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 O(1)O(1)O(1) 的时间内完成 get 或者 put 操作。具体的方法如下:
对于 get 操作,首先判断 key 是否存在:
如果 key 不存在,则返回 −1-1−1;
如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 O(1)O(1)O(1),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)O(1)O(1)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 O(1)O(1)O(1) 时间内完成。
小贴士
在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
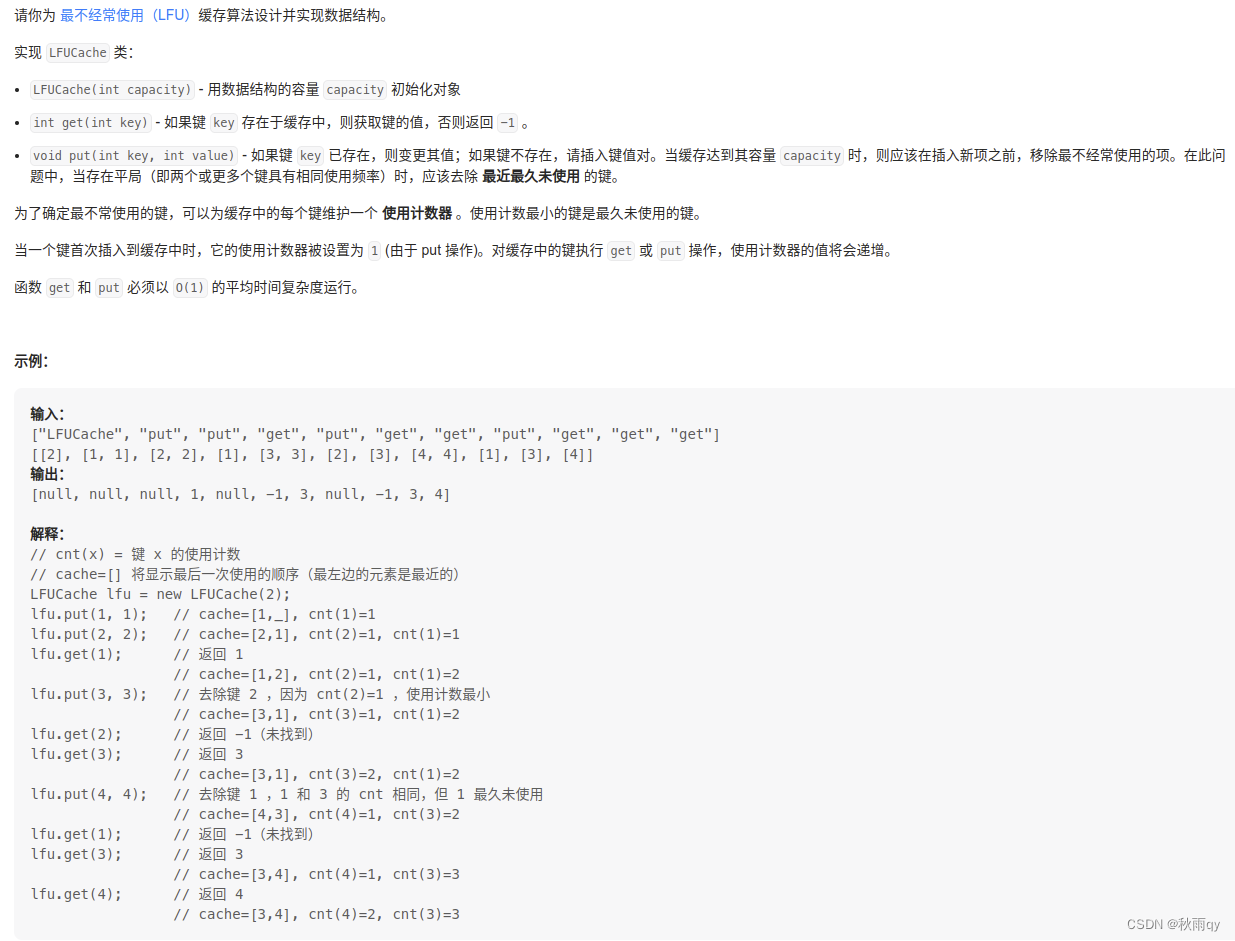
460 LFU 缓存算法
最不经常使用算法(LFU):这个缓存算法使用一个计数器来记录条目被访问的频率。通过使用LFU缓存算法,最低访问数的条目首先被移除。这个方法并不经常使用,因为它无法对一个拥有最初高访问率之后长时间没有被访问的条目缓存负责。