纸上得来终觉浅，绝知此事要躬行。前面 5 篇文章介绍了机器学习相关的部分基础知识，在本章，笔者将讲解基于 TensorFlow 实现一个简单的线性回归模型，以便增强读者对机器学习的体感。

目录

1.环境准备

1.1 安装 Python3

1.2 安装 PyCharm

1.3 安装 TensorFlow

1.4 安装 pandas

1.5 安装 matplotlib

2.编程实现

2.1 导入依赖模块

2.2 定义构建和训练模型的函数

2.3 定义打印函数

2.4 定义数据集

2.5 指定超参数

3.参数调优

3.1 默认超参数下训练

 3.2 优化超参数-epochs

 3.3 优化超参数-learning_rate

3.4 优化超参数-batch_size

4.小结

---

1.环境准备

在进行机器学习编程练习之前，我们需要准备好环境。在本节，笔者以 MacOS 为例，简单介绍环境准备的相关事项，Windows 也差不多。

1.1 安装 Python3

Mac 操作系统自带 Python，通常是 Python2.7，在终端输入命令：python -V，即可查看 Python 的版本号。虽然 Mac 自带的 Python，但它并不满足机器学的需要，在终端输入命令：python，可以看到如下信息——很显然，我们需要安装 Python3。

$ python

WARNING: Python 2.7 is not recommended. 
This version is included in macOS for compatibility with legacy software. 
Future versions of macOS will not include Python 2.7. 
Instead, it is recommended that you transition to using 'python3' from within Terminal.

在 Mac 上安装 Python 非常简单，直接前往 Python 官网：Python Releases for macOS | Python.org，下载相应版本的 Python 安装包即可。需要注意的是，对于采用苹果自研 M 系列 CPU 的 Mac，需要采用带有 “universal2 installer” 字样的安装包。下载安装包之后，双击安装即可，非常简单，网上也有很多资料，这里不再赘述。

1.2 安装 PyCharm

PyCharm 是大名鼎鼎的 JET Brains 公司开发的一款开源 Python IDE，是目前最受欢迎的 Python IDE 之一，功能强大，使用简单。

 PyCharm 的安装同样简单，安装包下载 官网地址：下载PyCharm：JetBrains为专业开发者提供的Python IDE，下载安装包后，根据指导安装即可。

1.3 安装 TensorFlow

TensorFlow 是当前人工智能主流开发工具之一，是谷歌于 2015 年 11 月 9 日正式开源的计算框架，是基于由 Jeff Dean 领头的谷歌大脑团队基于谷歌内部第一代深度学习系统 DistBelief 改进来的通用计算框架，在 GitHub 和工业界有较高的应用程度和实用度。

TensorFlow 中所有的计算都被转化为计算图上的节点，而节点之间的边描述了计算之间的依赖关系。张量(tensor)是 TensorFlow 基础的数据模型。TensorFlow 的名字已经说明了它最重要的两个概念——Tensor 和 Flow。Tensor 就是张量，我们可以理解成多维数组，零阶张量表示标量(scalar)，也就是一个数；第一阶张量为一个向量(vector)，也就是一个一维数组；第 n 阶张量可以理解为一个 n 维数组。Flow 翻译成中文就是 “流”，它直观地表达了张量之间通过计算相互转化的过程。TensorFlow 中对张量的实现并不是直接采用数组的形式，它只是对 TensorFlow 中运算结果的引用。关于 TensorFlow，在后面的文章中，笔者将会详细介绍，本文不展开。

安装 TensorFlow 的方法有很多，可以直接通过 pip 安装，命令如下（采用阿里云的镜像）：

pip3 install --index-url https://mirrors.aliyun.com/pypi/simple/ tensorflow-macos

也可以在 PyCharm 中直接安装：PyCharm -> Preference -> Python Interpreter ,点击 “+” ，搜索 TensorFlow 选择对应的版本安装，如下图所示：

1.4 安装 pandas

与安装 TensorFlow 类似，可以采用命令安装，也可以通过 PyCharm 安装。命令形式如下：

pip3 install --index-url https://mirrors.aliyun.com/pypi/simple/ pandas

1.5 安装 matplotlib

与安装 TensorFlow 类似，可以采用命令安装，也可以通过 PyCharm 安装。命令形式如下：

 pip3 install --index-url https://mirrors.aliyun.com/pypi/simple/ matplotlib

2.编程实现

2.1 导入依赖模块

import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt

2.2 定义构建和训练模型的函数

以下代码定义了两个函数：

• build_model（my_learning_rate），它构建一个空模型。
• train_model（模型、特征、标签、迭代），它根据传递的示例（特征和标签）训练模型。

本节不展开介绍模型构建代码，这里隐藏了此代码单元，如果读者感兴趣，可以点击对应的函数进一步查看模型构建细节。

# 定义构建模型的函数
def build_model(my_learning_rate):
    # 基于TensorFlow 创建并编译一个简单的线性回归模型
    model = tf.keras.models.Sequential()
    # 描述模型的拓扑
    # 这里采用的是一个简单线性回归模型，它是一个单层单个节点模型
    model.add(tf.keras.layers.Dense(units=1,
                                    input_shape=(1,)))
    # 编译模型 
    # 损失函数采用 MSE（mean_squared_error，均方根误差）
    model.compile(optimizer=tf.keras.optimizers.experimental.RMSprop(learning_rate=my_learning_rate),
                  loss="mean_squared_error",
                  metrics=[tf.keras.metrics.RootMeanSquaredError()])
    return model


# 定义一个训练模型的函数
def train_model(model, feature, label, epochs, batch_size):
    # 将特征值和标签值输入到模型。该模型将基于给定的周期数量（epochs）和批大小（batch_size）训练
    history = model.fit(x=feature,
                        y=label,
                        batch_size=batch_size,
                        epochs=epochs)

    # 收集经过训练的模型的权重和偏差。
    trained_weight = model.get_weights()[0]
    trained_bias = model.get_weights()[1]

    # 将周期（也称为“轮”）列表与历史的其余部分分开存储
    epochs = history.epoch

    # 收集每个周期的历史（快照）
    hist = pd.DataFrame(history.history)

    # 收集模型在每个周期的均方根误差。 
    rmse = hist["root_mean_squared_error"]

    return trained_weight, trained_bias, epochs, rmse

2.3 定义打印函数

我们使用一个名为 Matplotlib 的 Python 库来创建以下两个图：

• 特征值与标签值的关系图以及训练模型的输出的线
• 损失曲线

关于 Matplotlib 本节不展开介绍。读者可以自行搜索资料学习。打印函数的代码如下所示：

 根据训练特征和标签将训练模型可视化（打印出来）
def plot_the_model(trained_weight, trained_bias, feature, label):
    # 标记坐标轴
    plt.xlabel("feature")
    plt.ylabel("label")

    # 打印特征和标签.
    plt.scatter(feature, label)

    # 打印一条红线代表模型，起点和终点分别为 (x0, y0) 和 (x1, y1).
    x0 = 0
    y0 = trained_bias
    x1 = feature[-1]
    y1 = trained_bias + (trained_weight * x1)
    plt.plot([x0, x1], [y0, y1], c='r')

    # 渲染散点图和红线
    plt.show()


# 绘制损失曲线，显示损失与周期（训练轮数）的关系
def plot_the_loss_curve(epochs, rmse):
    plt.figure()
    # X轴为训练周期数，Y轴为损失（此处采用用MSE计算损失）
    plt.xlabel("Epoch")
    plt.ylabel("Root Mean Squared Error")

    plt.plot(epochs, rmse, label="Loss")
    plt.legend()
    plt.ylim([rmse.min() * 0.97, rmse.max()])
    plt.show()

2.4 定义数据集

既然要训练模型，那么就需要“示例”数据，本节我们人为定义一组简单的“示例”数据，如下所示：

my_feature = ([1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0])
my_label = ([5.0, 8.8, 9.6, 14.2, 18.8, 19.5, 21.4, 26.8, 28.9, 32.0, 33.8, 38.2])

2.5 指定超参数

根据前面几篇文章的介绍，我们知道，训练线性回归模型相关的超参数有三个，如下：

• 学习率：learning_rate
• 周期：epochs
• 批量_大小：batch_size

下面的代码初始化这些超参数，然后调用构建和训练模型的函数。

# 初始化超参数
learning_rate = 0.01
epochs = 10
my_batch_size = 12

# 构建、训练模型
my_model = build_model(learning_rate)
trained_weight, trained_bias, epochs, rmse = train_model(my_model, my_feature,
                                                         my_label, epochs,
                                                         my_batch_size)
# 打印模型，将其可视化，便于观察训练效果
plot_the_model(trained_weight, trained_bias, my_feature, my_label)
plot_the_loss_curve(epochs, rmse)

3.参数调优

基于第二节（编程实现），我们可以得到完整的代码，如下所示：

import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt


# 定义构建模型的函数
def build_model(my_learning_rate):
    # 基于TensorFlow 创建并编译一个简单的线性回归模型
    model = tf.keras.models.Sequential()
    # 描述模型的拓扑
    # 这里采用的是一个简单线性回归模型，它是一个单层单个节点模型
    model.add(tf.keras.layers.Dense(units=1,
                                    input_shape=(1,)))
    # 编译模型
    # 损失函数采用 MSE（mean_squared_error，均方根误差）
    model.compile(optimizer=tf.keras.optimizers.experimental.RMSprop(learning_rate=my_learning_rate),
                  loss="mean_squared_error",
                  metrics=[tf.keras.metrics.RootMeanSquaredError()])
    return model


# 定义一个训练模型的函数
def train_model(model, feature, label, epochs, batch_size):
    # 将特征值和标签值输入到模型。该模型将基于给定的周期数量（epochs）和批大小（batch_size）训练
    history = model.fit(x=feature,
                        y=label,
                        batch_size=batch_size,
                        epochs=epochs)

    # 收集经过训练的模型的权重和偏差。
    trained_weight = model.get_weights()[0]
    trained_bias = model.get_weights()[1]

    # 将周期（也称为“轮”）列表与历史的其余部分分开存储
    epochs = history.epoch

    # 收集每个周期的历史（快照）
    hist = pd.DataFrame(history.history)

    # 收集模型在每个周期的均方根误差。
    rmse = hist["root_mean_squared_error"]

    return trained_weight, trained_bias, epochs, rmse


print("Defined build_model and train_model")


# 根据训练特征和标签将训练模型可视化（打印出来）
def plot_the_model(trained_weight, trained_bias, feature, label):
    # 标记坐标轴
    plt.xlabel("feature")
    plt.ylabel("label")

    # 打印特征和标签.
    plt.scatter(feature, label)

    # 打印一条红线代表模型，起点和终点分别为 (x0, y0) 和 (x1, y1).
    x0 = 0
    y0 = trained_bias
    x1 = feature[-1]
    y1 = trained_bias + (trained_weight * x1)
    plt.plot([x0, x1], [y0, y1], c='r')

    # 渲染散点图和红线
    plt.show()


# 绘制损失曲线，显示损失与周期（训练轮数）的关系
def plot_the_loss_curve(epochs, rmse):
    plt.figure()
    # X轴为训练周期数，Y轴为损失（此处采用用MSE计算损失）
    plt.xlabel("Epoch")
    plt.ylabel("Root Mean Squared Error")

    plt.plot(epochs, rmse, label="Loss")
    plt.legend()
    plt.ylim([rmse.min() * 0.97, rmse.max()])
    plt.show()


print("Defined the plot_the_model and plot_the_loss_curve functions.")

my_feature = ([1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0])
my_label = ([5.0, 8.8, 9.6, 14.2, 18.8, 19.5, 21.4, 26.8, 28.9, 32.0, 33.8, 38.2])

# 初始化超参数
learning_rate = 0.01
epochs = 10
my_batch_size = 12

# 构建、训练模型
my_model = build_model(learning_rate)
trained_weight, trained_bias, epochs, rmse = train_model(my_model, my_feature,
                                                         my_label, epochs,
                                                         my_batch_size)
# 打印模型，将其可视化，便于观察训练效果
plot_the_model(trained_weight, trained_bias, my_feature, my_label)
plot_the_loss_curve(epochs, rmse)

3.1 默认超参数下训练

在 PyCharm 中执行上述代码，可以得到如下结果：很明显——模型并不能准确地刻画示例数据集的特点，因此，损失较大，且未收敛。

 3.2 优化超参数-epochs

理想情况下，训练损失应该稳步减少，先是急剧减少，然后再慢慢减少。最终，训练损失应该保持稳定（零斜率或接近零斜率），这表明训练已经收敛。

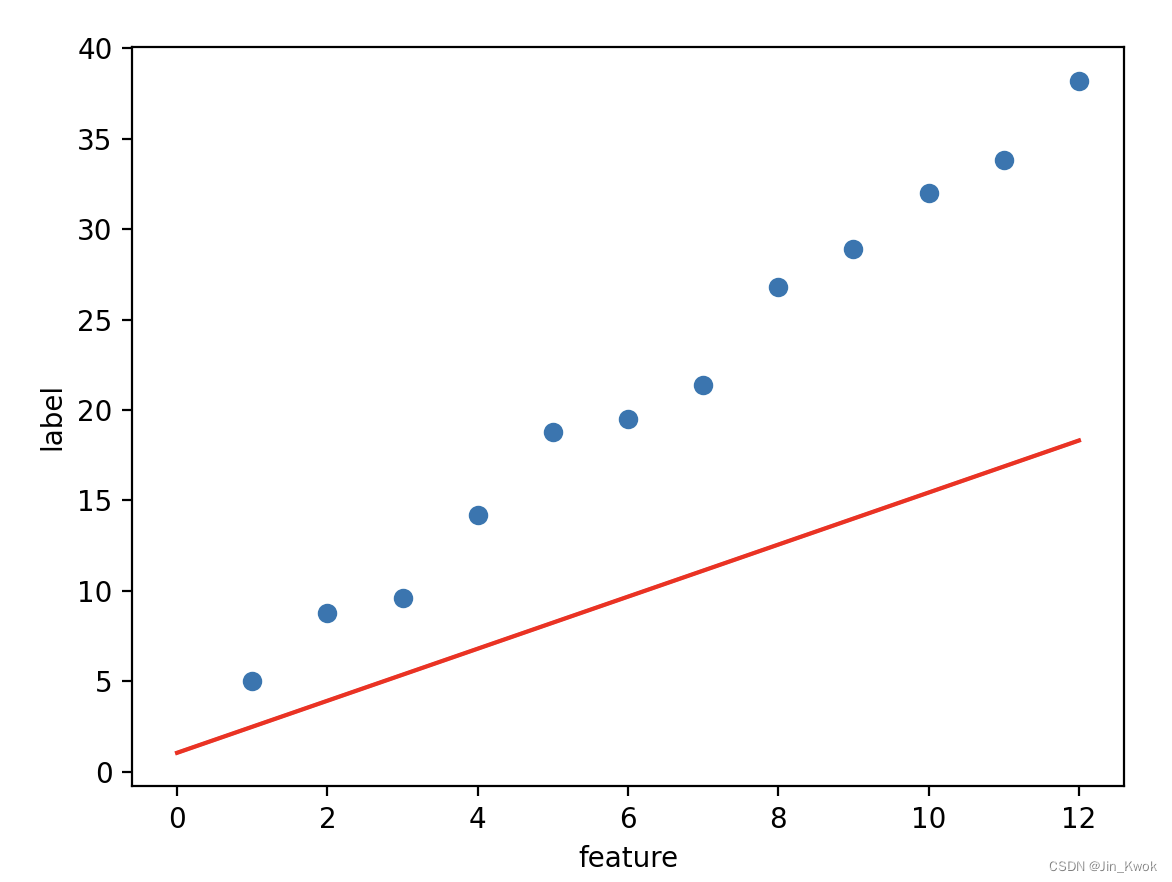
在 3.1 中，训练损失没有收敛。一个可能的解决方案是——增加训练周期的数量，进行训练，以使模型收敛。然而，这种方法是低效的。将 epochs 增加至 100，其他参数不变，训练结果如下——很明显，训练出的模型要优于默认参数。

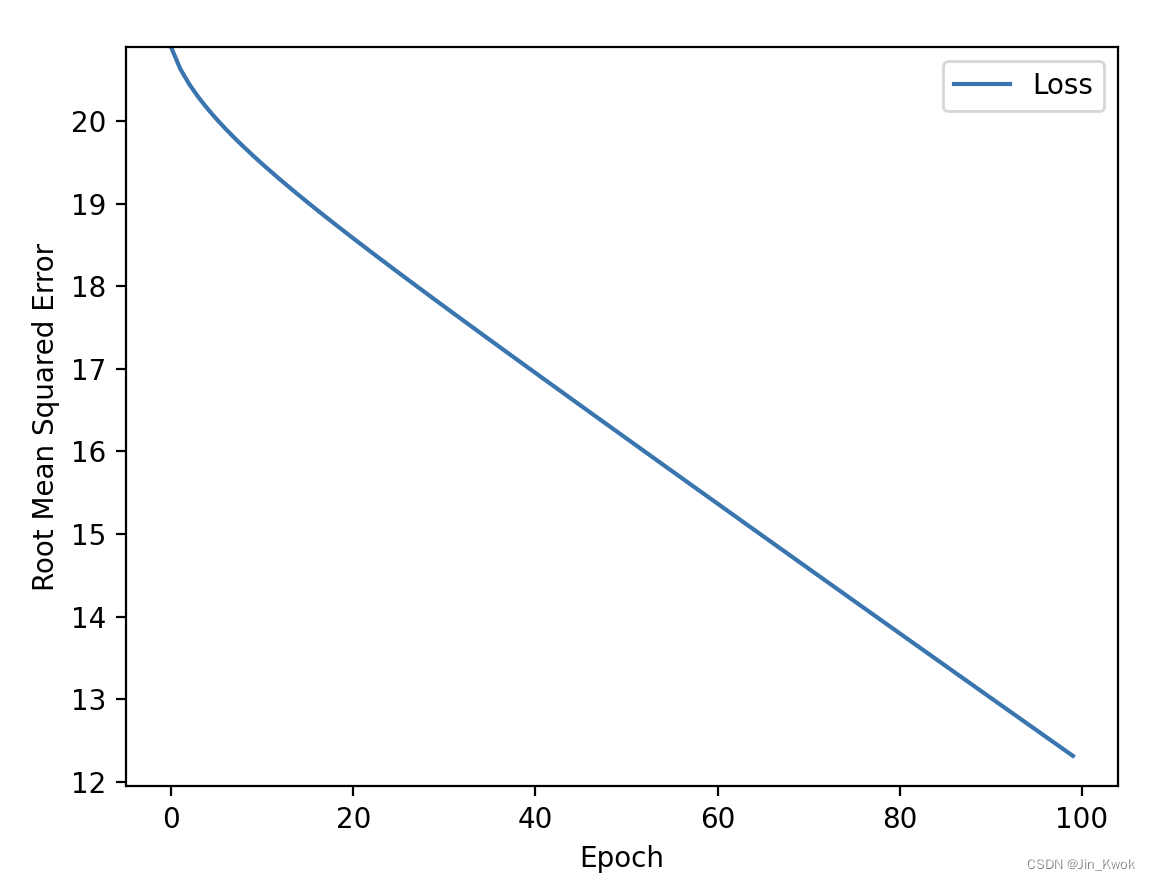
 更进一步，我们将 epochs 增加至 300，其他参数不变，训练结果如下——虽然更好了，但仍旧没有有效收敛，不难想象，只要继续增加 epochs ，训练出的模型会越来越好，但是，这并不划算。

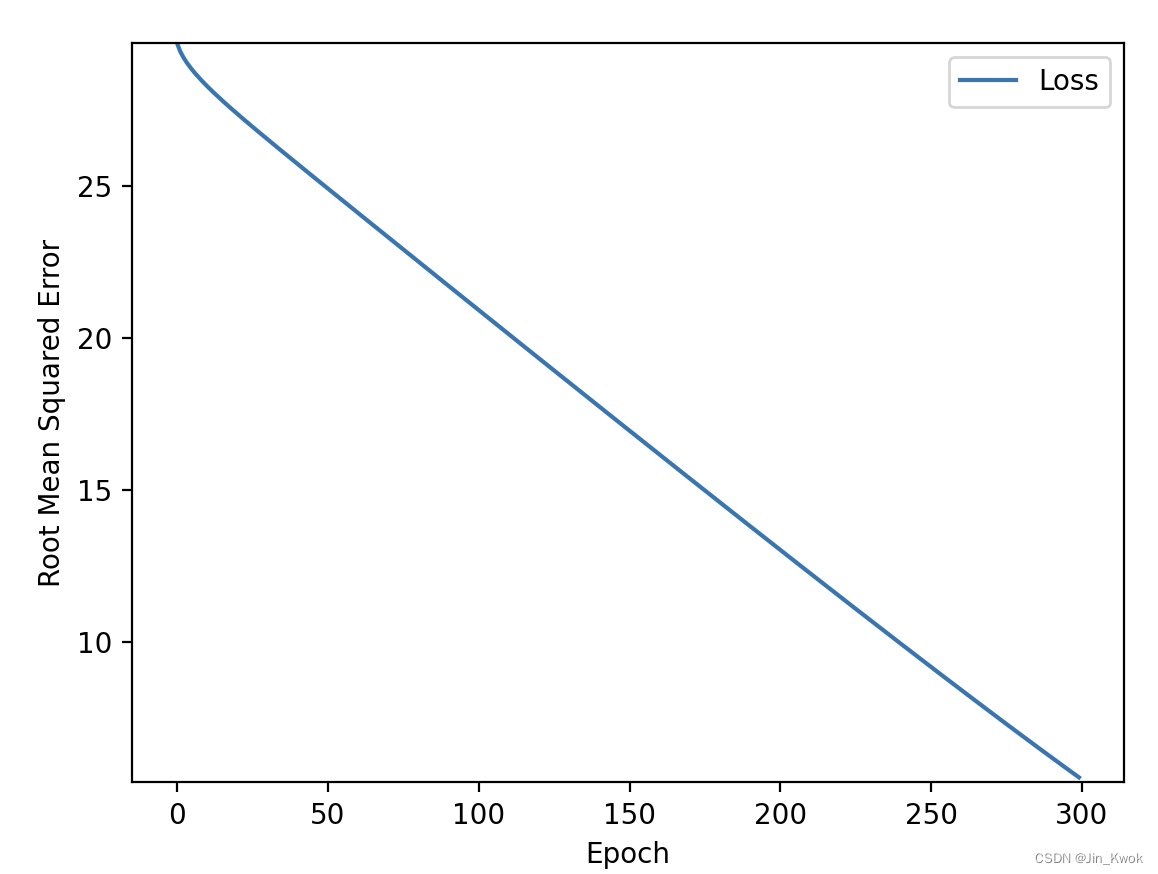
 3.3 优化超参数-learning_rate

 在前面的几篇文章中，笔者已经介绍中学习率的定义，它代表“步长”。在上面的例子中，收敛非常慢，损失曲线相对平缓，因此，增加“步长”-learning_rate 应该有助于加速收敛，我们来测试一下。将 learning_rate 增加为 0.1，epochs 为 50，训练结果如下：很明显，训练快速收敛。

 

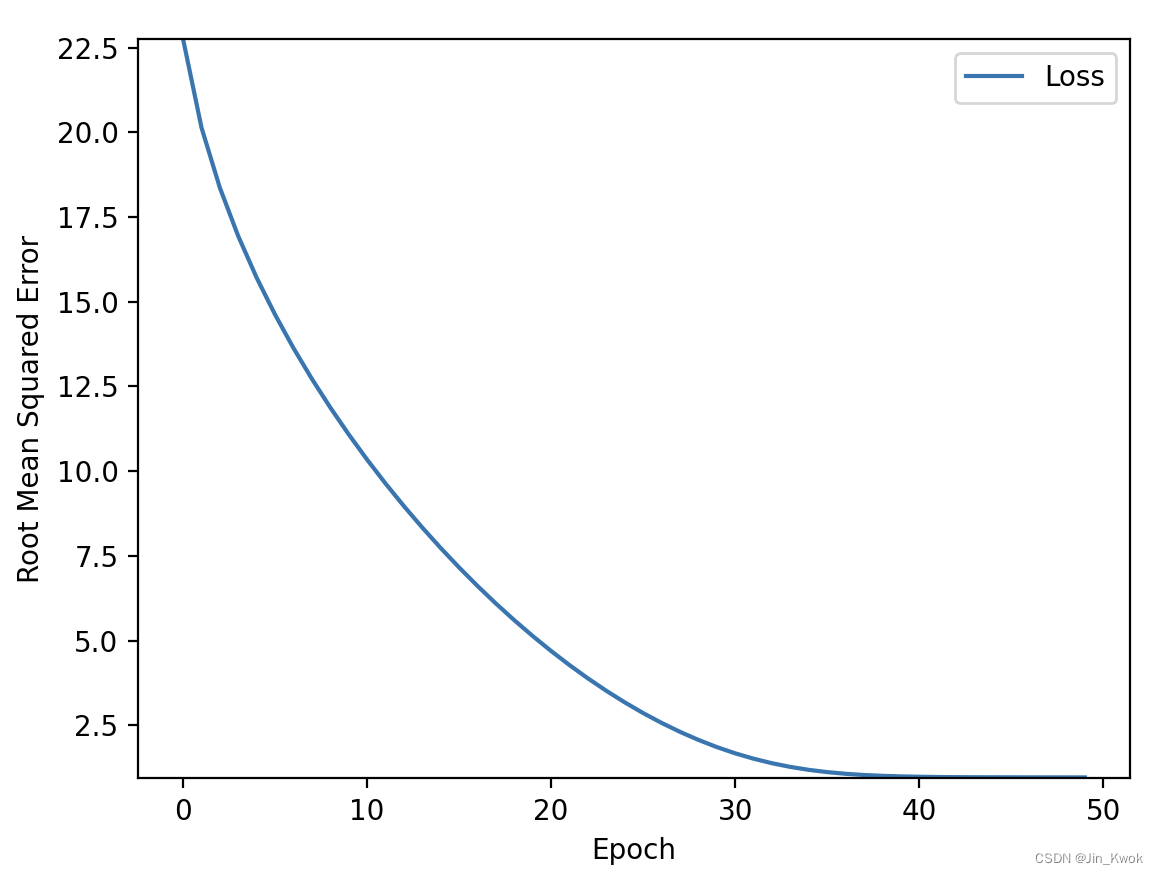
增大学习率有效地加速了收敛，那么学习率是不是越大越好呢？根据前面几篇文章的介绍，我们知道，学习率过大将会导致模型无法收敛。我们将 learning_rate 增加为 5，epochs 为 50，其他参数不变，训练结果如下：很明显，损失大幅波动，难以收敛。

 

在本案例中，epochs = 70，learning_rate = 0.14 可以较快收敛。

3.4 优化超参数-batch_size

系统重新计算模型的损失值，并在每次迭代后调整模型的权重和偏差。每次迭代都是系统处理一个批次的时间跨度。例如，如果批量大小为 6，则系统重新计算模型的损失值，并在每 6 个示例进行处理后调整模型的权重和偏差。

一个周期跨越足够的迭代来处理数据集中的每个示例。例如，如果批量大小为12，则每个周期持续一次迭代。然而，如果批量大小为 6，则每个周期消耗两次迭代。

在上面的代码中，我们简单地将批量大小设置为数据集中的示例数（在本例中为 12 个）是很诱人的。然而，该模型实际上可能在较小的批次上训练得更快，当然，非常小的批次可能不包含足够的信息来帮助模型收敛。

在以下代码单元中试调整 batch_size。看看 batch_size 设置的最小整数是多少，并且仍然使模型在一百个时期内收敛？

简单地，将 batch_size 设置为 1，learning_rate 设置为 0.14，epochs 设置为 10，训练结果如下：很明显，收敛得非常快，仅仅 10 个周期，训练出的模型已经非常优秀了。

 

 

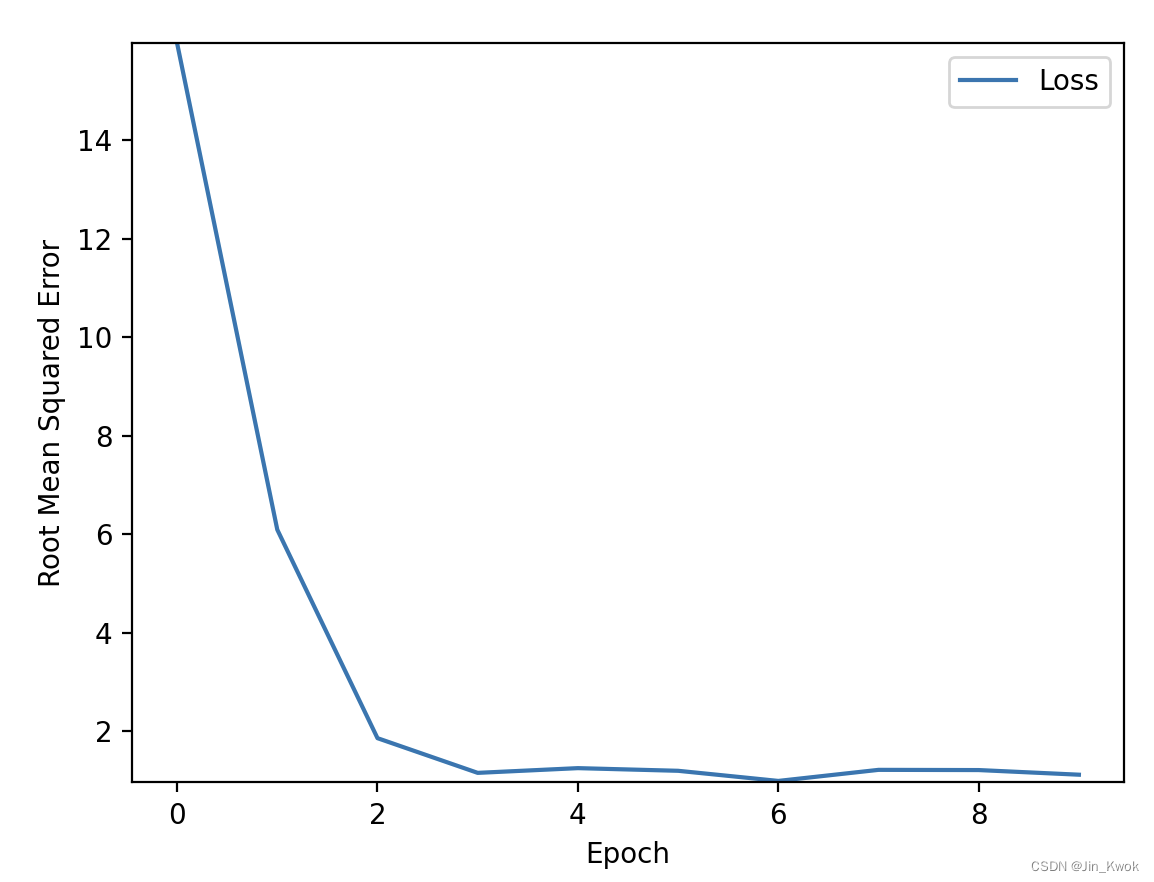
4.小结

大多数机器学习问题都需要大量的超参数调整。不幸的是，我们不能为每个模型提供具体的调优规则。降低学习率可以帮助一个模型有效地收敛，但会使另一个模型收敛得太慢。在实践中，必须进行反复实验，为数据集找到最佳的超参数集。也就是说，以下是一些经验法则：

• 训练损失应该稳步减少，先是急剧减少，然后再缓慢减少，直到曲线的斜率达到或接近零。
• 如果训练损失没有收敛，那就训练更多的时期。
• 如果训练损失减少得太慢，请提高学习率。请注意，将学习率设置得过高也可能会阻止训练损失的收敛。
• 如果训练损失变化很大（即训练损失四处跳跃），则降低学习率。
• 在增加周期数量或批量大小的同时降低学习率通常是一个很好的组合。
• 将批次大小设置为非常小的批次号也可能导致不稳定。首先，尝试大批量值。然后，减小批处理大小，直到出现降级。

对于由大量示例组成的真实世界数据集，整个数据集可能无法放入内存。在这种情况下，需要减小批大小，以使批能够适应内存。须知：超参数的理想组合是依赖于数据的，因此必须始终进行实验和验证。