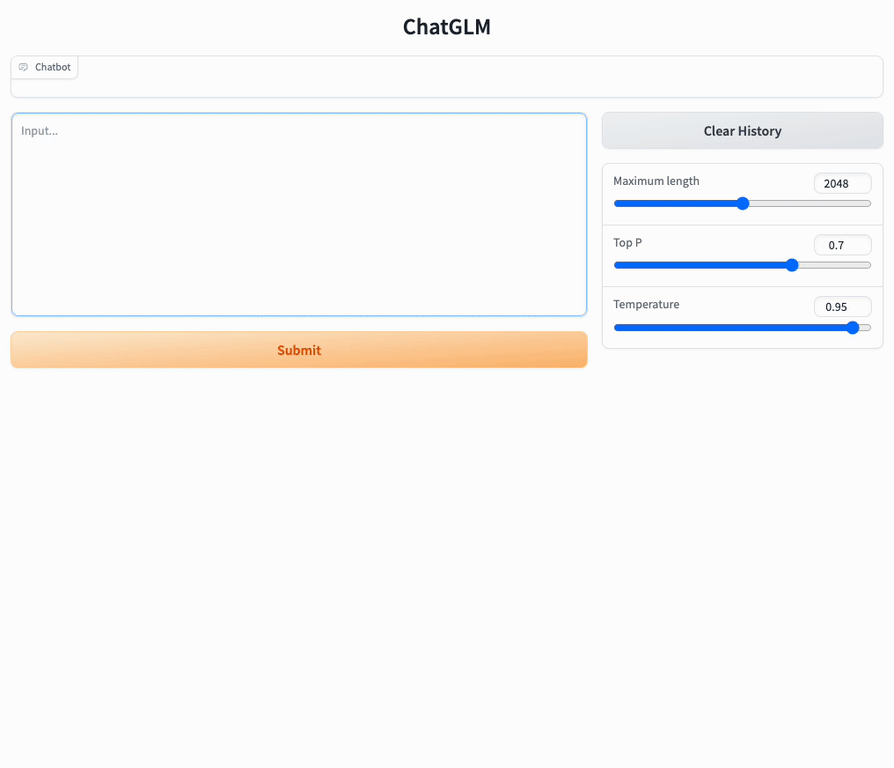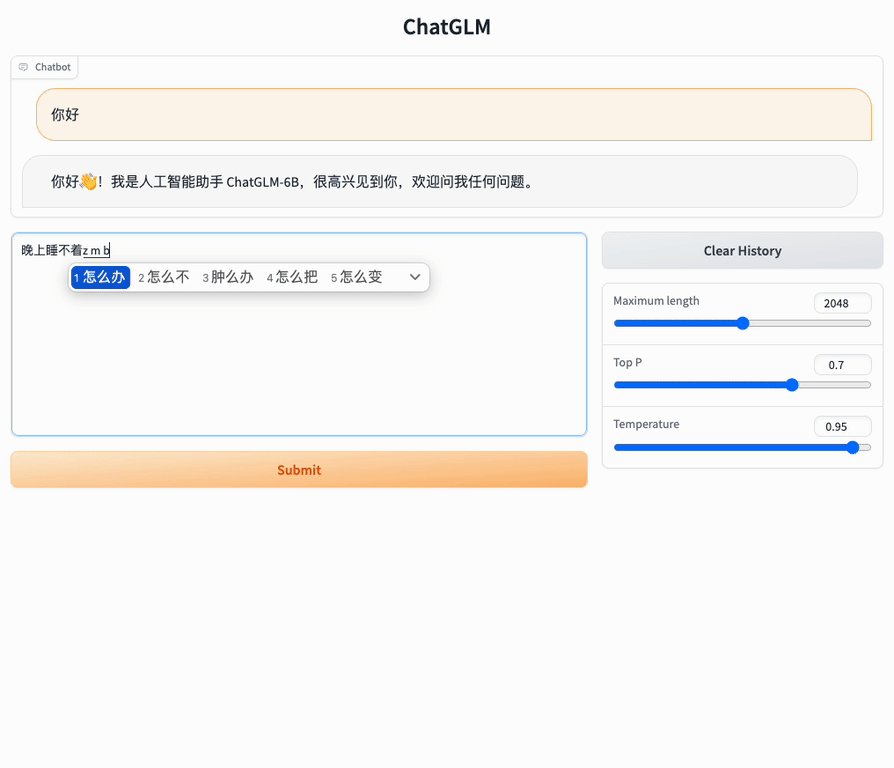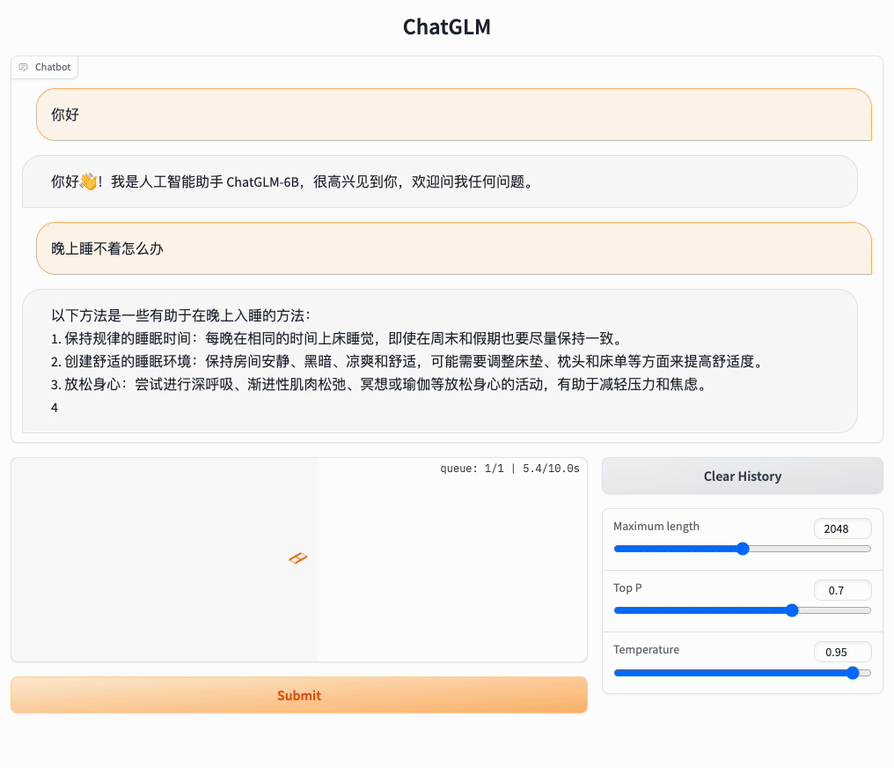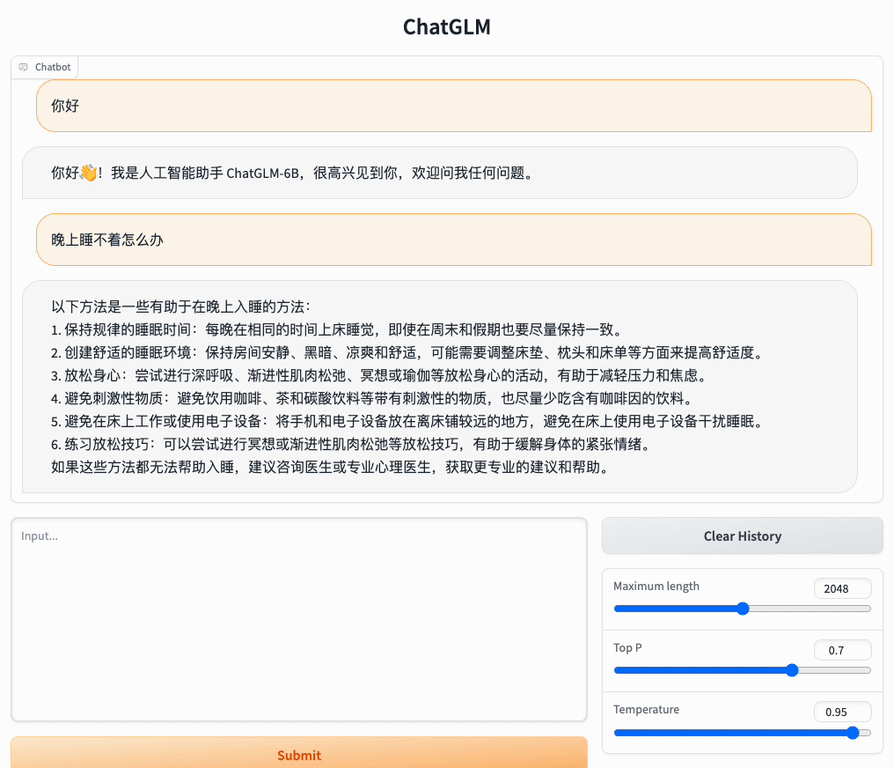
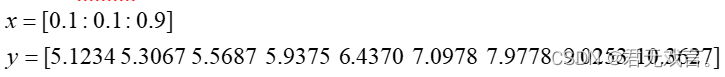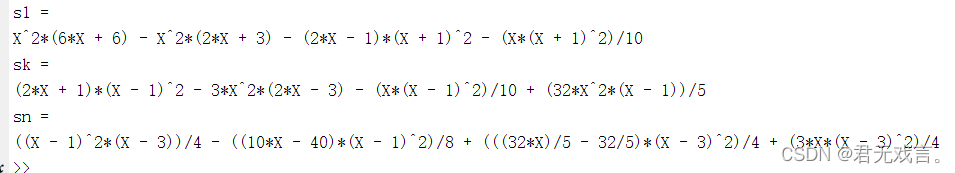| 实验目的及要求:
1、会在Matlab平台上进行样条插值; 2、会在Matlab平台上进行最小二乘拟合。 | ||||||||||||||||||
| 实验内容: 1、利用spline函数绘制【0,10】内步长为1的插值节点处的 2、根据下列数据三转角方程法构造三次样条函数S(x),,并写出表达式。
3、利用polyfit函数作三次,四次多项式拟合,并描绘拟合曲线。拟合数据如下:
| ||||||||||||||||||
| 实验步骤与程序:
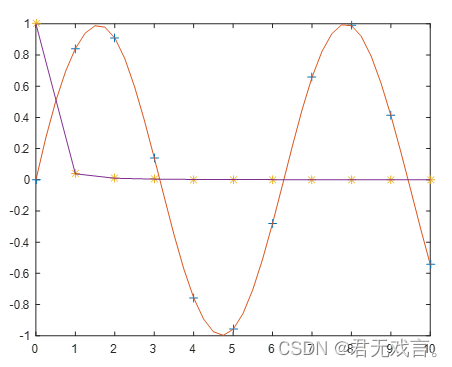
x=0:10; y=sin(x); xx=0:0.25:10; yy=spline(x,y,xx) plot(x,y,'+',xx,yy) hold on
x=0:10; y=1./(1+25*x.^2); xx=0:1:10; yy=spline(x,y,xx); plot(x,y,'*',xx,yy)
被调用的san_zhuan_jiao.m文件 function [a,c,b,A,dY,s1,sk,sn] = san_zhuan_jiao(x,y,x0,y0,dy0,dyn) n = length(x); A = zeros(n-1,n-1); a = zeros(n-1,1); b = zeros(n-1,1); c = zeros(n-1,1); h = zeros(n-1,1); h0 = x(1) - x0 ; for i = 1:n-1 h(i) = x(i+1)-x(i); end a(1) = h0/(h0 + h(1)); c(1) = 1-a(1); b(1) = 3*((c(1)*(y(1)-y0)/h0)+a(1)*(y(2)-y(1))/(h(1))); for i = 2:n-1 a(i) = h(i-1)/(h(i-1)+h(i)) c(i) = i-a(i); b(i) = 3*(c(i)*(y(i)-y(i-1)/h(i-1))+a(i)*(y(i+1)-y(i))/h(i)) end b(1) = b(1)-c(1)*dy0; b(n-1) = b(n-1)-a(n-1)*dyn; A(1,1) = 2; A(1,2) = a(1); for i = 2:n-2 A(i,i) = 2; A(i,i+1) = a(i); A(i,i-1) = c(i); end A(n-1,n-1) = 2; A(n-1,n-1) = c(n-1); dY = A\b; syms X s1=y0*(h0-2*x0+2*X)*(X-x(1))^2/h0^3+y(1)* (h0+2*x(1)-2*X)*(X-x0)^2/h0^3+dy0*(X-x0)*(X-x(1))^2/h0^2+dY(1)*(X-x(1))*(X-x0)^2/h0^2; for k=2:n-1 sk=y(k-1)*((h(k-1)-2*x(k-1)+2*X)*(X-x(k))^2)/(h(k-1)^3)+y(k)*((h(k-1)+2*x(k)-2*X)*(X-x(k-1))^2)/(h(k-1)^3)+dY(k-1)*((X-x(k-1))*(X-x(k))^2)/(h(k-1)^2)+dY(k)*((X-x(k))*(X-x(k-1))^2)/(h(k-1)^2); end sn=y(n-1)*(h(n-1)-2*x(n-1)+2*X)*(X-x(n))^2/h(n-1)^3+y(n)* (h(n-1)+2*x(n)-2*X)*(X-x(n-1))^2/h(n-1)^3+dY(n-1)*(X-x(n-1))*(X-x(n))^2/h(n-1)^2+dyn*(X-x(n))*(X-x(n-1))^2/h(n-1)^2;
x0=-1;y0=-1;x=[0 1 3];y=[1 3 5]; dy0=6;dyn=1; [a,c,b,A,dY,s1,sk,sn]=san_zhuan_jiao(x,y,x0,y0,dy0,dyn)
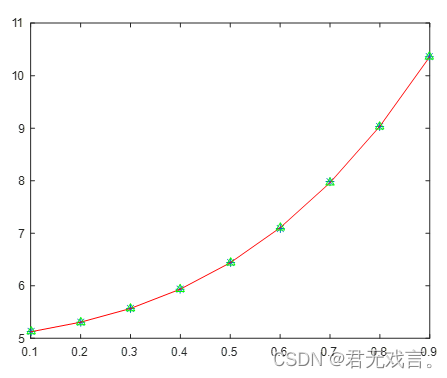
x=0.1:0.1:0.9; y=[5.1234 5.3067 5.5687 5.9375 6.4370 7.0978 7.9778 9.0253 10.3627]; a1=polyfit(x,y,3) a2=polyfit(x,y,4) x1=0.1:0.1:0.9; y1=a1(4)+a1(3)*x1+a1(2)*x1.^2+a1(1)*x1.^3; %(y1=polyval(a1,x1) y2=a2(5)+a2(4)*x1+a2(3)*x1.^2+a2(2)*x1.^3+a2(1)*x1.^4; %(y2=polyval(a2,x1) plot(x,y,'*') hold on %三次多项式拟合 plot(x1,y1,'r-') hold on %四次多项式拟合 plot(x1,y2,'g^') | ||||||||||||||||||
| 运行结果:
| ||||||||||||||||||
| 结果分析与讨论: 1.spline函数只能实现非节点边界和约束导数的第二边界条件,可以实现一维或者高维的曲线插值。 2.polyfit函数是matlab中用于进行曲线拟合的一个函数。其数学基础是最小二乘法曲线拟合原理。 3.三次样条插值,是通过一系列形值点的一条光滑曲线,数学上通过求解三弯矩方程组得出曲线函数组的过程 | ||||||||||||||||||
数学建模算法(基于matlab和python)之 三次样条插值与多项式拟合(2/10)
news2026/2/12 18:41:28
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/691278.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Linux命令大全(面试必备)
前两节有说Git命令,反馈还不错,看来大家对这些必备的命令还挺感兴趣哈,这节就罗列一些Linux必须掌握的命令。 干货满满哦,直接发车... 一、常用的基本命令 1、关机开机 关机 shutdown-h now
立刻关机shutdown-h 3
3分钟后关机…
Java八股文面试(黑马)
Redis篇 数据库的并发不高,请求到了一定的量就会击垮数据库,导致宕机。 大概率是客户端正好在写入数据,sentinel与当前master出现分区 而 重新选举了一个master Mysql篇
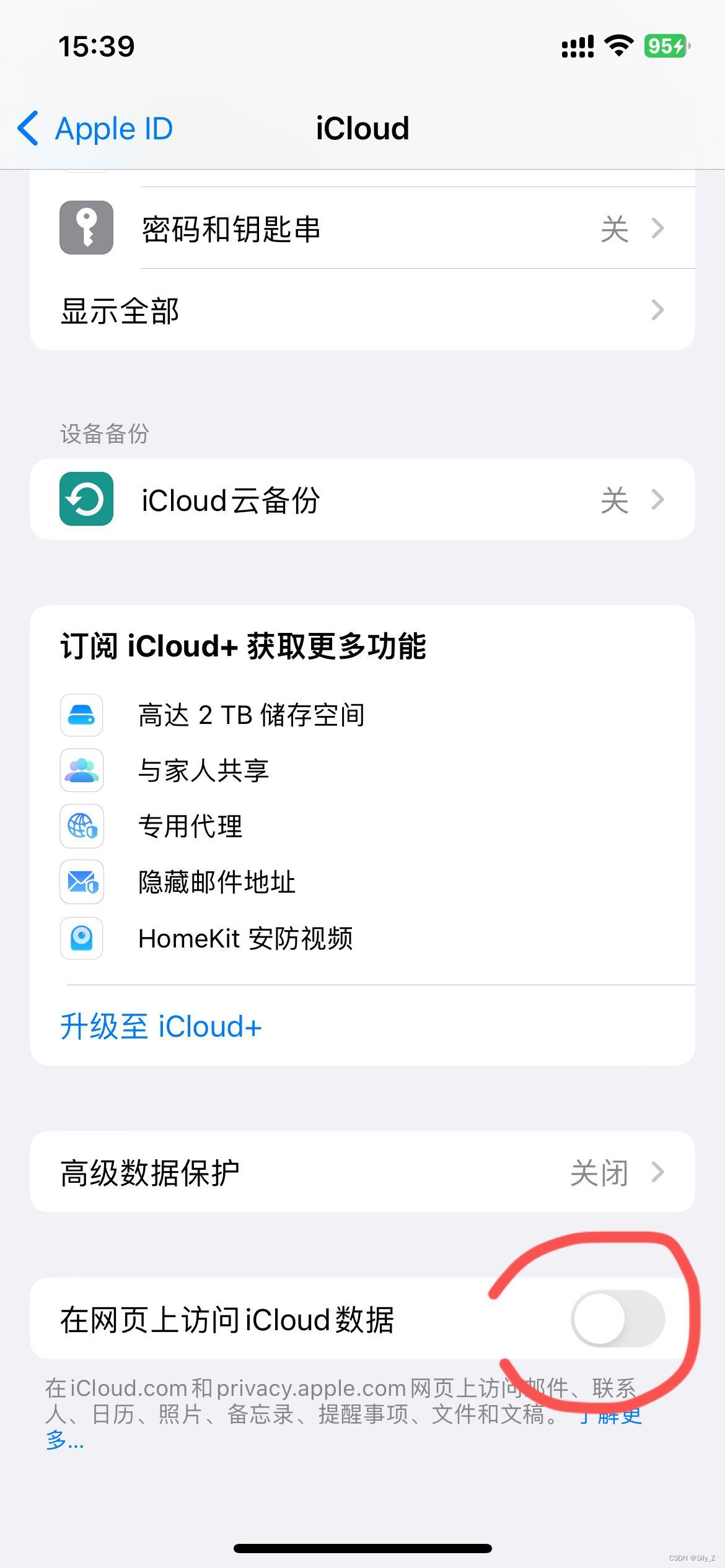
IOS 手机抓包 频繁 访问 gateway.icloud.com.cn:443
在抓包的时候,有时候苹果手机在重启后频繁出现gateway.icloud.com.cn:443请求 这种情况需要在手机上进行设置,适用于IOS16.0以上版本,其他版本不清楚,没有尝试过 进入 设置--点击AppleID ,进入个人信息页面---点击iCl…
开发工具-网络测试工具 POSTMAN 的脚本使用
开发工具-网络测试工具 POSTMAN 的脚本使用 postman 脚本应用基础设置变量、获取变量示例环境变量的使用测试 发送请求示例常用的变量、方法responseBody 获取响应体内容pm.response 获取响应信息pm.expect() JSON检查cheerio.load() 类似于 jquery 操作 html 元素 POSTMAN 是网…
做独立站要选择什么样的产品呢?这些要点要注意!
跨境圈都在说独立站能不能成功七分靠选品,三分靠运营,可见选品是决定独立站能不能成功的一大关键因素,只有先选定了产品,才能进行店铺装修、物流设置,以及后续的运营工作。
那么独立站的卖家应该如何去选品呢…
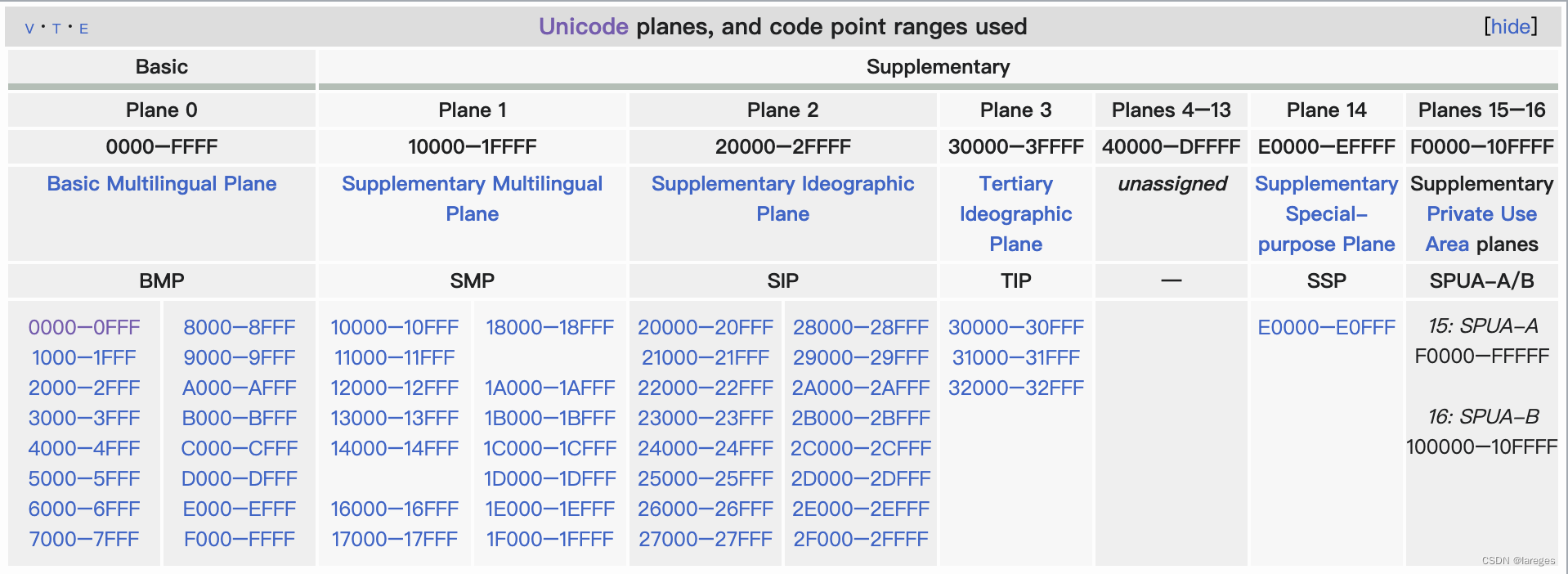
一文搞懂ASCII、Unicode与UTF-8
目录 一、前置知识二、ASCII三、从ASCII到Unicode四、Unicode五、UTF-8六、总结References 一、前置知识
一个字节有8-bit;一个十六进制数占4-bit,故一个字节可以表示为两个十六进制数(通常会加上 0x 前缀);十六进制通…
基于Python+OpenCV的视频字符化(深度学习+机器视觉)含全部工程源码
目录 前言总体设计系统整体结构图系统流程图 运行环境Python 环境OpenCV环境 模块实现1. 视频读取及处理2. 色素块识别与替换3. 视频合成4. 操作系统上的实现 系统测试工程源代码下载其它资料下载 前言
本项目利用 OpenCV 提供的轻量、高效的 C类和 Python 接口,实…
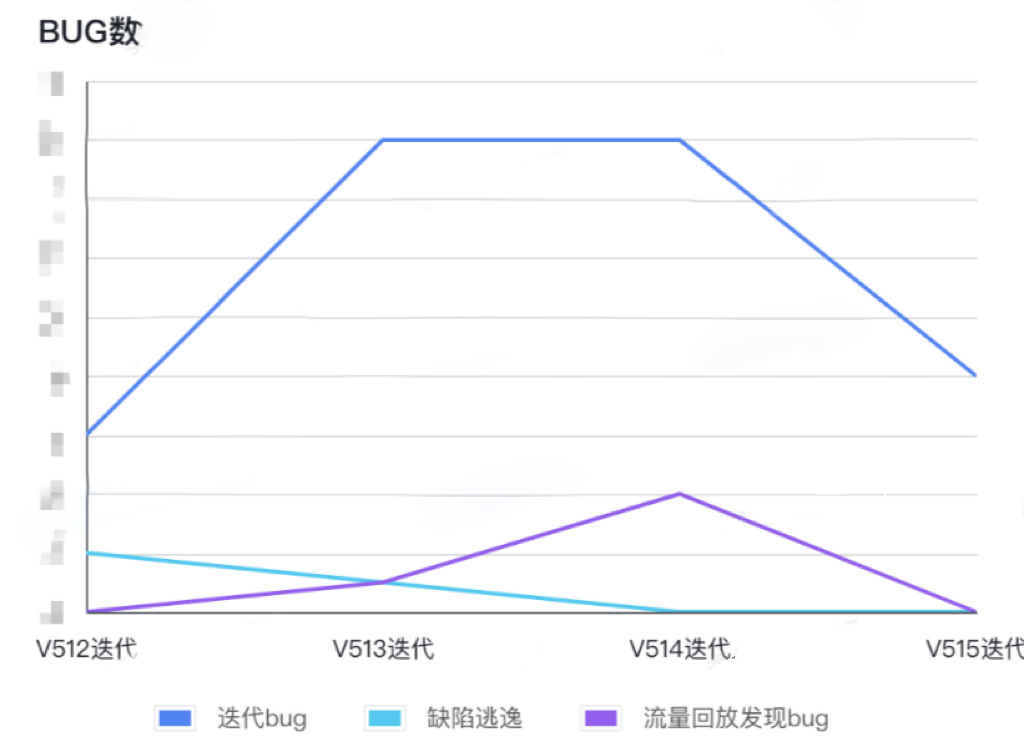
数据平台流量回放最佳实践|精选
1.1 数据平台业务背景
数据平台利用大数据智能分析、数据可视化等技术,对公司内外部经过采集、建设、管理、分析的多源异构数据进行呈现和应用,实现了数据共享、日常报表自动生成、快速和智能分析,深度挖掘数据价值,满足企业各级…
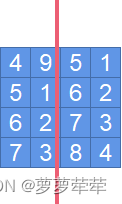
Leetcode48 旋转图像
给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]]
输出…
ZYNQ——按键消抖实验
文章目录 原理简介软件仿真板上验证 原理简介
按键作为基本的人机输入接口,在很多电子设计中都是比较常见的,但是由于其机械特性,在按键按下或者松开的时候,按键的输入值是有抖动的。按键的抖动是其固有特性,因此无论…
打死也不要进外包,来看看我在腾讯外包的这2年......
我18年毕业于一个普通二本学校,是一个很不出名的小本科。大学期间专业知识也没有去认真的学习,所以毕业的时候就随便找了一份工作,在一个小公司做功能测试。
记得那时候薪资大概是6k左右,因为是在工厂,工作环境很差&a…
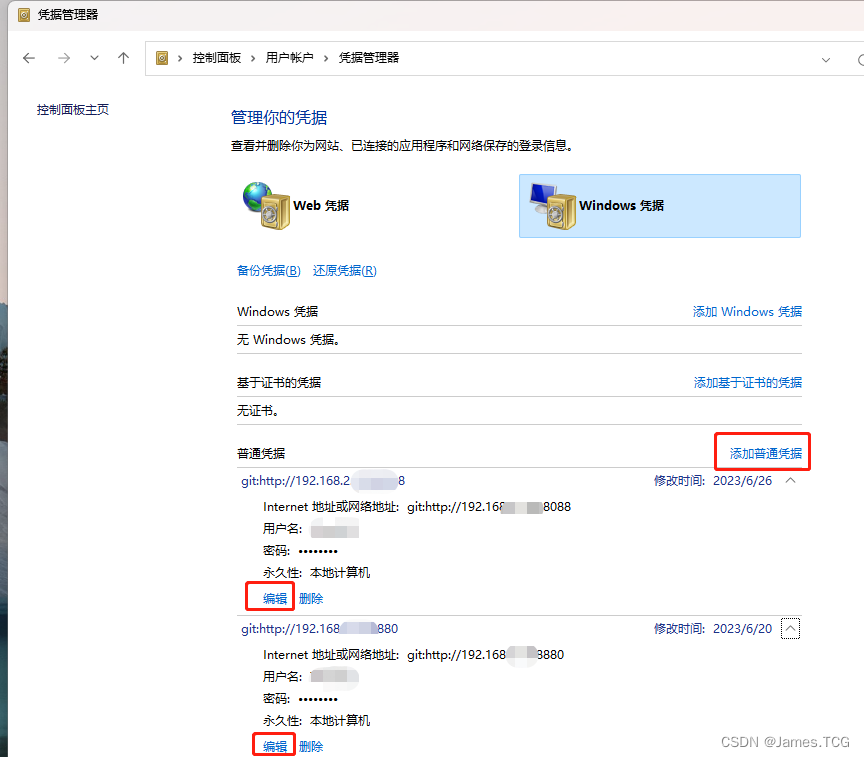
Gitlab 访问令牌更新 替换
引言
访问令牌到期后如何丝滑更换,或则如何更改账户的访问令牌实现权限变动呢?在我们使用访问令牌克隆项目之后,Windows凭据就帮我们记录下了密码。当然密码是不可见的,只能进行删除重新设置,通过凭据管理器进行更改。…
python基于预训练大模型权重实现文本向量化开发构建微博评论数据情感极向识别模型
因为最近的一些项目涉及到了大模型相关的技术开发研究,在我前面的博文中也已经有一些实践记录学习资料分享的文章了,今天是在做模型训练的时候突然想到一个有意思的想法,按照我之前做文本分类的方法,基本主流的技术路线都是先对文…
性能提升571%,32K超长上下文,推理速度提升42%,允许商用,国产开源大模型推出了二代 ChatGLM2-6B...
6月份是火热的夏天,各种火热的 AI 产品也在密集的更新,天越热,大家是干得热火朝天,卷出了新高度。 前有现在大火的 ChatGPT,ChatGPT 更新:大杀器!函数调用示范,ChatGPT 3.5/4 双双升…
Java Web JDBC(2)23.6.26
3.6 PreparedStatement PreparedStatement作用: 预编译SQL语句并执行:预防SQL注入问题 3.6.1 代码模拟SQL注入问题
Test
public void testLogin() throws Exception {//2. 获取连接:如果连接的是本机mysql并且端口是默认的 3306 可以简化书…
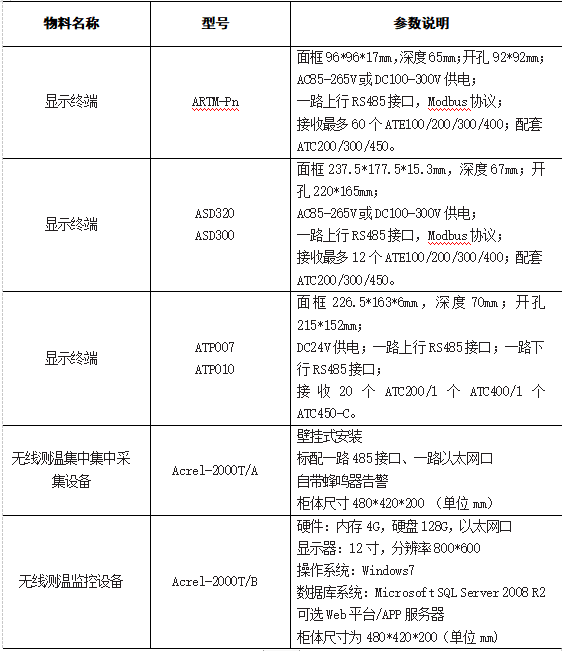
浅谈无线温度监测系统在冶炼厂供配电的应用
安科瑞 华楠 摘要:高压供配电系统运行稳定性与电气元器件连接点温度密切相关,通过与传统测温方法对比,实时在线无线温度监测解决 了密封高压开关柜内部各连接点温度无法检测的难题,满足了供电系统安全稳定运行的要求,降…
redis 主从复制 哨兵 安装部署
学习开始前先了解一下 Redis是一个开源的内存数据结构存储系统,它支持多种数据结构,如字符串、哈希表、列表、集合、有序集合等。Redis最大的特点是数据存储在内存中,因此读写速度非常快,同时也支持数据持久化,可以将数…
吐血整理,接口自动化测试-Config配置文件框架封装(实战)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言
configparser的介…
阿里巴巴2023最新版Spring Security王者晋级文档
Spring 是一个非常流行和成功的 Java 应用开发框架。Spring Security 是 Spring 家族中的一个安全管理框架,提供了一套 Web 应用安全性的完整解决方案。在用户认证方面,Spring Security 框架支持主流的认证方式,包括 HTTP 基本认证、HTTP 表单…
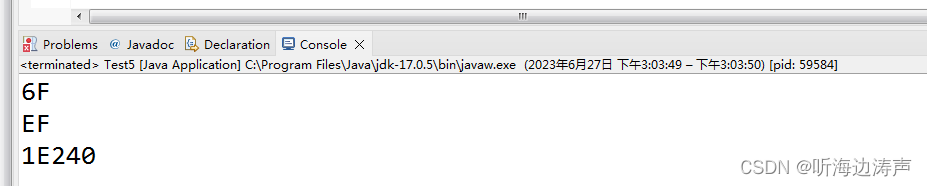
输出一个数的十六进制表示
可以使用Integer.toHexString、Long.toHexString得到数值的十六进制表示。 下面的代码示例列出了几种情况:
public class Test5 {public static void main(String[] args) {byte b1 0b01101111; System.out.println(Integer.toHexString(b1).toUpperCase());byte…
 的样条曲线。
的样条曲线。