MarchineCubes定义

是一种基于体素构建三维模型的方式，有些类似《我的世界》中的堆方块，但实际上，建模是以方块之间的交点为中心点，每个cube表示八个象限的相交模型

实现思路

在三维空间中划分网格，每个网格是一个cube，其8个顶点各有两个状态{in、out}，分别表示该顶点是否位于三维模型的内部
根据这8个顶点的状态，可确定当前cube自身的模型，这个排列组合正好是一个8位二进制
这里需要对这8个顶点进行约定，为后续代码提供方便
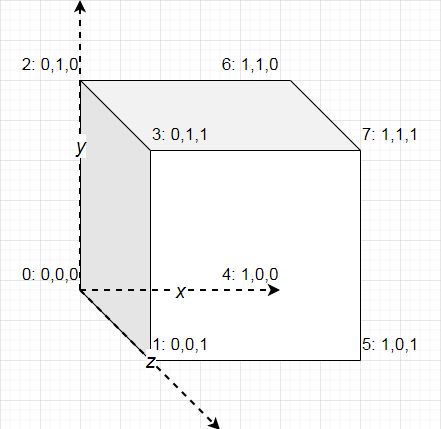这样约定的好处是，某些临边、对角位置可用二进制位运算方便获取，临边是相应位异或、对角是按位取反

Cube建模

总共有255种组合，其中有些是重复形状的翻转、和旋转，且0x00、0xff实际上是空模型，那么一个cube就需要254个模型，我没有采用Polygonising中的三角形列表，而是用python在maya中建模

import maya.cmds as cmd
for i in range(1,255):
    names=[]
    for j in range(0,8):
        if 1<<j&i:
            names.append("aaa%d_%d"%(i,j))
            # 若相邻顶点{in、out}状态不同就w、h、d=0.9是故意在模型中间留条缝
            cmd.polyCube(w=1<<(1<<2^j)&i and 1 or 0.9,h=1<<(1<<1^j)&i and 1 or 0.9,d=1<<(1<<0^j)&i and 1 or 0.9,n=names[-1])
            cmd.move((1<<2&j and 0.5 or -0.5),1<<1&j and 0.5 or -0.5,1<<0&j and 0.5 or -0.5)
    if len(names)>1:
        cmd.polyCBoolOp(names,n="aaa%d"%(i))
    elif len(names)>0:
        cmd.rename(names[-1],"aaa%d"%(i))
    if len(names)>0:
        cmd.makeIdentity("aaa%d"%(i),a=1,t=1)

这样就建立好1~254所有模型，并重叠摆在原点中心。然后清空历史，选中所有模型，手动将模型上、下、左、右、前、后0.5米之外的部分切割掉

切割前	切割后

切割之后，就是一个1x1单位中心对齐的模型，再通过脚本将其一字排开

for i in range(1,255):
    cmd.move(i*1.5,0,0,"aaa%d"%(i))

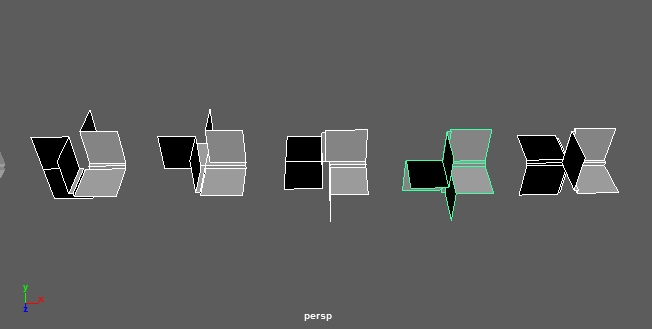在Outliner中可以看到每个mesh被命名为aaa1 ~ aaa254，方便后续引擎中按索引直接取出对应模型

数据结构及伪代码

这里采用自研引擎+lua环境实现
由于lua数组实际是hash结构，所以可以将网格中的三维坐标转为一个整形数值用来做hash key，也就没必要存储为三维数组了

-- id表示为三维空间坐标，由于double有效数为9007199254740992，所以用1024^3足够，哈希值：x*1024^2+y*1024+z
function coordToId(x,y,z)
    return x*1024^2+y*1024+z
end

-- 那么当某个hash反推：x=math.floor(v/1024/1024)、y=math.floor(v/1024%1024)、z=v%1024
function idToCoord(id)
    return math.floor(id/1024/1024),math.floor(id/1024%1024),id%1024
end

定义grids、cubes数据

function EditorBehavior:__init(name)
    ...
    self.grids={}
    self.cubes={}
end

grids表示网格的交点坐标
cubes表示围绕交点周围的模型，也就是说cubes在每一维度都比grids多一个单位
当修改某个grids的状态，in：1、out：nil

function EditorBehavior:AddGrid(x,y,z)
    self.grids[coordToId(x,y,z)]=1
    self:UpdateTileRoundTheGrid(x,y,z,true)
end

function EditorBehavior:RemoveGrid(x,y,z)
    self.grids[coordToId(x,y,z)]=nil
    self:UpdateTileRoundTheGrid(x,y,z,false)
end

然后根据这个grids内容更新周围八个象限cubes的状态值，若某个cube更新后数值为0，则清除这个cube

function EditorBehavior:UpdateTileRoundTheGrid(x,y,z,inside)
    for i=0,1 do for j=0,1 do for k=0,1 do
        local pos=i*4+j*2+k
        local ipos=bit.band(bit.bnot(pos),0x7)
        local mask=bit.lshift(0x1,ipos)
        local cube=self.cubes[coordToId(x+i,y+j,z+k)]
        if cube then
            if inside then
                self.cubes[coordToId(x+i,y+j,z+k)]=bit.bor(cube,mask)
            else
                cube=bit.band(cube,bit.bnot(mask))
                if 0==cube then
                    self.cubes[coordToId(x+i,y+j,z+k)]=nil
                else
                    self.cubes[coordToId(x+i,y+j,z+k)]=cube
                end
            end
        else
            if inside then
                self.cubes[coordToId(x+i,y+j,z+k)]=mask
            end
        end
    end end end
end

在渲染时，将所有cube的状态值，以及模型渲染出来
这里cube的状态值，正好对应之前maya中模型的aaa1 ~ aaa254

参考

https://www.cs.carleton.edu/cs_comps/0405/shape/marching_cubes.html
http://paulbourke.net/geometry/polygonise/
https://www.researchgate.net/publication/202232897_Marching_Cubes_A_High_Resolution_3D_Surface_Construction_Algorithm
https://www.bilibili.com/video/BV1yJ411r73v