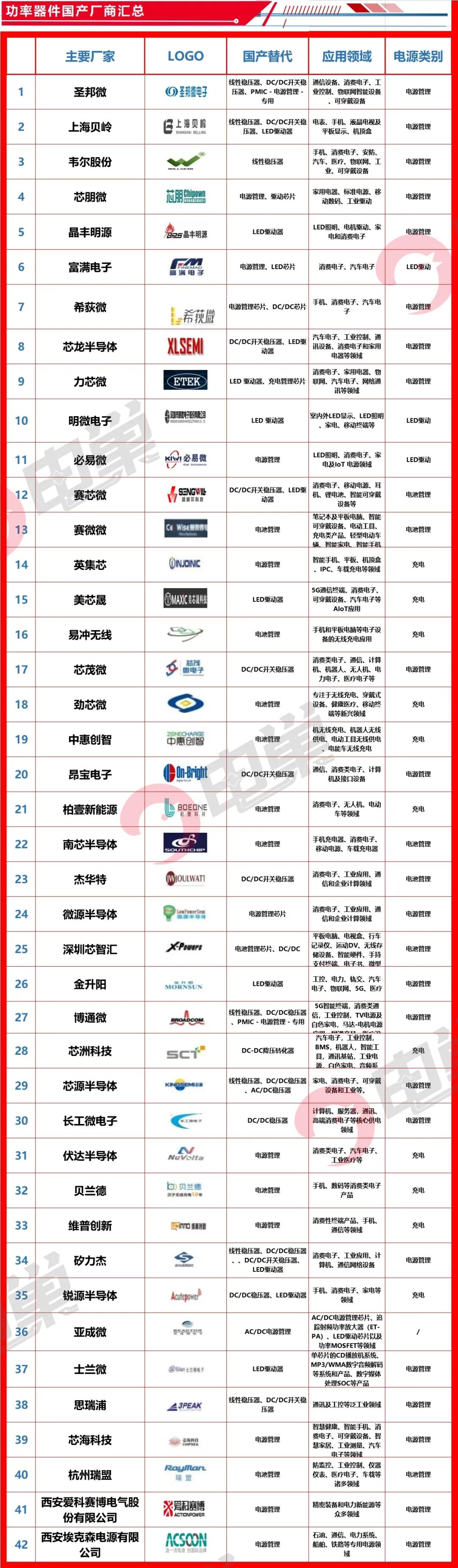
通过深度学习框架的高级API也能更方便地实现softmax回归模型。

继续使用Fashion-MNIST数据集，并保持批量大小为256。

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

1. 初始化参数模型

softmax回归的输出层是一个全连接层。 因此，为了实现我们的模型， 我们只需在Sequential中添加一个带有10个输出的全连接层。 同样，在这里Sequential并不是必要的， 但它是实现深度模型的基础。 我们仍然以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状
# 因此，我们定义了展平层（flatten）在线性层前调整网络输入的形状
# 把展平层和线性层串在一起放到Sequential中，就得到了network
net = nn.Sequential(nn.Flatten(),nn.Linear(784,10))

# 初始化权重W
def init_weights(m):# m就是当前的层layer
    if type(m) == nn.Linear:
        # 初始化weight为均值为0（默认），标准差为0.01
        nn.init.normal_(m.weight,std = 0.01)
        m.bias.data.fill_(0)
        
net.apply(init_weights) # 把init_weights函数apply到net上面
# 也就是，net的每一层都要调用/跑一下init_weights这个函数

ps：这个展平层的作用相当于在《从零实现softmax中》定义net函数中的reshape：

2.重新审视Softmax的实现

通过将softmax和交叉熵结合在一起，可以避免反向传播过程中可能会困扰我们的数值稳定性问题。

注意：在从零开始实现softmax中，是把规范化/归一化之后的预测，也就是softmax（o）之后得到的预测y传递到交叉熵损失函数中，而在这里，可以把softmax和交叉熵结合在一起，也就是传入未归一化的预测即可。（因为传递到softmax的参数就是未归一化的矩阵o，而此处把softmax和交叉熵损失结合在一起了）

loss = nn.CrossEntropyLoss(reduction='none')

ps：softmax在cross EntropyLoss里面

我们使用学习率为0.1的小批量随机梯度下降作为优化算法。 这与我们在线性回归例子中的相同，这说明了优化器的普适性。

trainer = torch.optim.SGD(net.parameters(),lr=0.1)

3. 训练

调用 之前定义的训练函数来训练模型

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

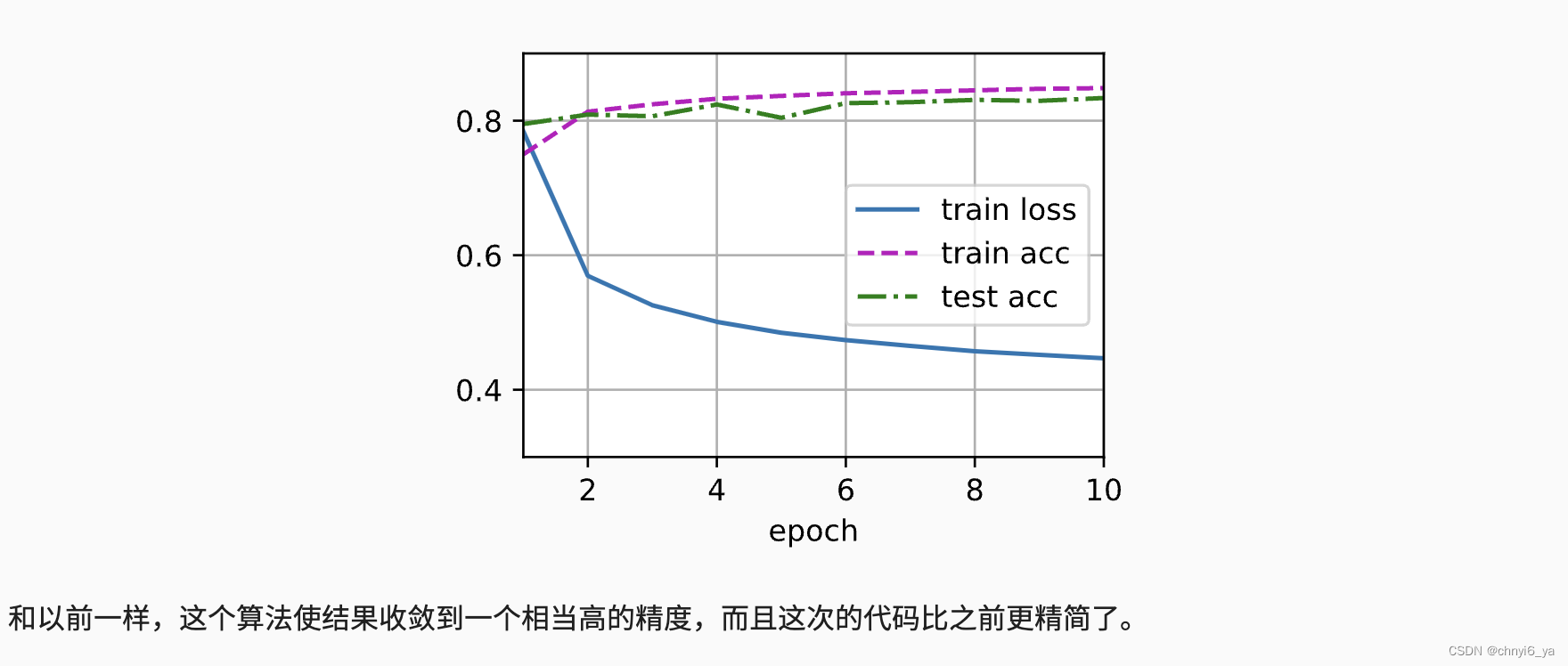
运行结果如下：