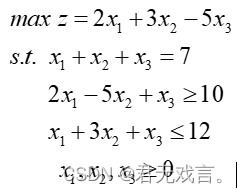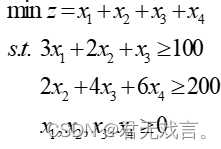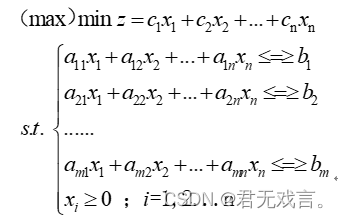| 一、实验目的: 1. 会建立合理的规划模型; 2. 学习掌握Matlab中求解线性规划的命令; [x,fval]=linprog(f,A,b); [x,fval]=linprog(f,A,b,Aeq,beq); [x,fval]=linprog(f,A,b,Aeq,beq,lb;ub); 3. 要求学生能在计算机上应用各种优化软件包熟练地操作,解决一些实际应用案例; 4. 预习求解线性规划的单纯形法的基本理论思想。 | ||||||||||||||||||||||||||||||||||||||||||
1.题目:求解线性规划问题:
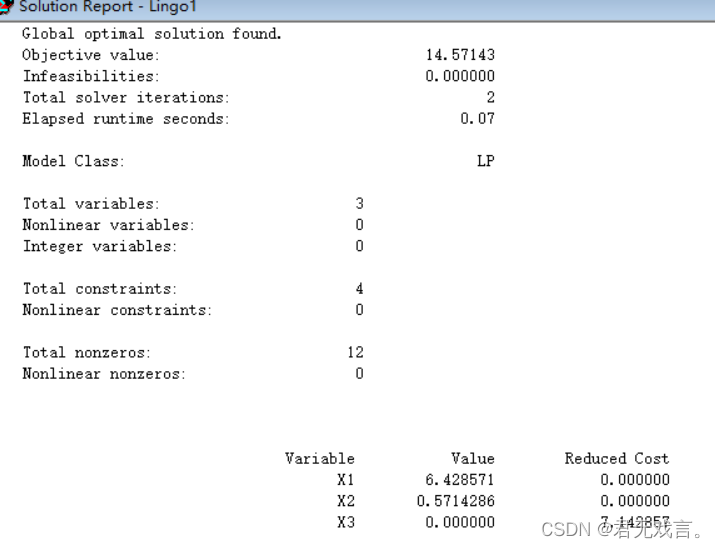
程序代码: MODEL: X1+X2+X3=7; 2*X1-5*X2+X3>10; X1+3*X2+X3<12; END !LINGO>符号相当于>= !LINGO<符号相当于<= !LINGO默认x1,x2>=0 程序执行结果:
结果解释: 当x1等于6.428571,x2等于0.5714286,x3等于0时,z取得最大为14.57143 2.题目:求解线性规划问题:
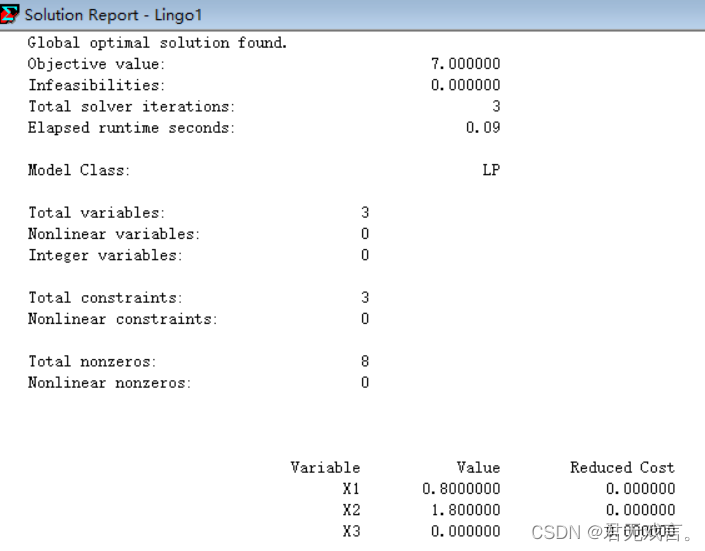
程序代码: MODEL: X1+4*X2+2*X3>8; 3*X1+2*X2>6; END !LINGO>符号相当于>= !LINGO<符号相当于<= !LINGO默认x1,x2,X3>=0 程序执行结果:
结果解释: 当x1等于0.8,x2等于1.8,x3等于0时,z取得最小为7 3.题目:某厂计划在下一个生产周期内生产甲、乙两种产品,需要消耗A1、A2、A3三种资源(例如钢材、煤炭和设备台时),已知每件产品对这三种资源的消耗,这三种资源的现有数量和每件产品可获得的利润如表所示。问如何安排生产计划,使得既能充分利用现有资源,又使总利润最大?
数学模型:设生产甲产品x1件,生产乙产品x2件,可以得到如下数学模型:
程序代码: MODEL: 5*X1+2*X2<170; 2*X1+3*X2<100; X1+5*X2<150; END !LINGO>符号相当于>= !LINGO<符号相当于<= !LINGO默认x1,x2>=0 程序执行结果:
结果解释: 当生产甲商品8件,乙商品28件时,总利润达到最大为584。 题目:4.求解线性规划问题:假定现有一批某种型号的圆钢长8m,需要截取2.5m的毛坯100根、长1.3m的毛坯200根,问应该怎样选择下料方式,才能既满足需要,又使总的下料最小? 数学模型:一根8M的圆钢截取成2.5m和1.3m的毛坯一共有X1,X2,X3,X4四种方案,具体如下:
由表可以得到如下数学模型:
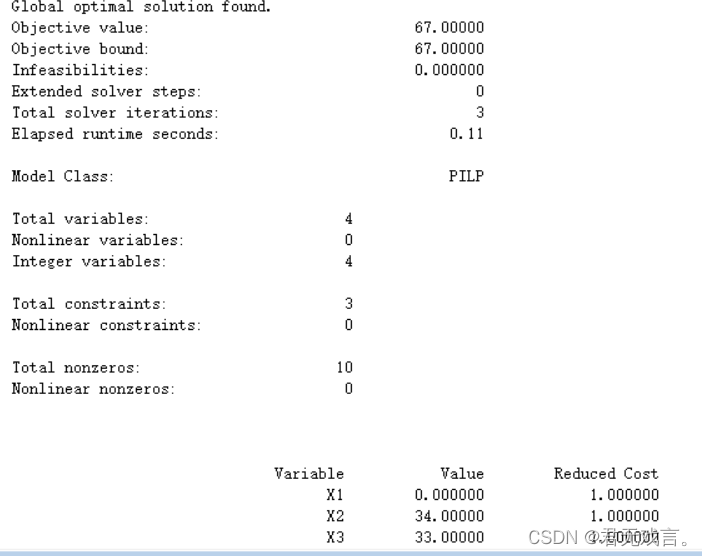
程序代码: MODEL: 3*X1+2*X2+X3>100; 2*X2+4*X3+6*X4>200; @GIN(X1); @GIN(X2); @GIN(X3); @GIN(X4); END !LINGO>符号相当于>= !LINGO<符号相当于<= !LINGO默认x1,x2,X3,X4>=0 !@GIN(X1)表示对进行整数约束 程序执行结果:
结果解释: 当执行x2方案34次,x3方案33次时使总下料最少为67。即用34根圆钢切割成68根2.5m的毛坯和1.3m的毛坯,再用33根圆钢切割成33根2.5m的毛坯和132根1.3m的毛坯使总下料最少为67根8m的圆钢。 | ||||||||||||||||||||||||||||||||||||||||||
| 分析与讨论:
①分析问题,找出决策变量。 ②找出等式或不等式约束条件。 ③构造关于决策变量的一个线性函数
| ||||||||||||||||||||||||||||||||||||||||||
最优化方法(基于lingo)之 求解线性规划问题(1/6)
news2026/2/12 6:21:55
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/690816.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
音视频流媒体开发工作机会占80%的市场份额
音视频流媒体开发领域的工作机会在过去几年中确实呈现出了快速增长的趋势。随着互联网的普及和网络带宽的提高,人们对音视频内容的需求也越来越大,这导致了许多公司和组织寻求音视频流媒体开发人员来满足市场需求。 音视频流媒体开发工作的主要流程可以概…
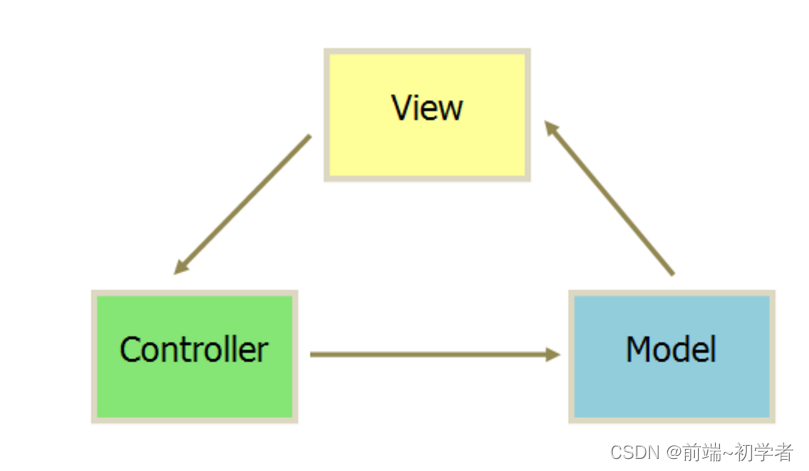
对MVVM和MVC开发模式的理解
对MVVM和MVC开发模式的理解 1、MVVM2、MVC3、MVVM与MVC的区别 1、MVVM
MVVM最早由微软提出来,它借鉴了桌面应用程序的MVC思想,在前端页面中,把Model用纯JavaScript对象表示,View负责显示,两者做到了最大限度的分离&am…
基于 SpringBoot 2.X 框架的智能制造云办公系统,已开源
简介
基于SpringBoot 2.X框架的智能制造云办公系统,立志打造ERP生产功能的软件,专注进销存财务功能生产管理,适合各行业。主要完成从下单->进货->生产->出库的过程,涉及到领料,出入库,工序&#…
Kotlin Multiplatform项目探索之KMChat
Kotlin Multiplatform项目探索之KMChat 这是当前在 Kotlin Multiplatform 官方文档中提议的用例结构。Kotlin Multiplatform 中包含的许多子组件已经发布了稳定版本,即使目前不稳定的组件也在迅速更新。
本文中的演示项目包括 Compose Multiplatform - Web (Experi…
【微服务架构设计和实现】4.9 微服务测试和部署最佳实践
往期回顾:
第一章:【云原生概念和技术】
第二章:【容器化应用程序设计和开发】
第三章:【基于容器的部署、管理和扩展】
第四章:【4.1 微服务架构概述和设计原则】
第四章:【4.2 服务边界的定义和划分…
STM32单片机(六)TIM定时器 -> 第二节:TIM定时中断练习2(定时器外部时钟)
❤️ 专栏简介:本专栏记录了从零学习单片机的过程,其中包括51单片机和STM32单片机两部分;建议先学习51单片机,其是STM32等高级单片机的基础;这样再学习STM32时才能融会贯通。 ☀️ 专栏适用人群 :适用于想要…
如何看待社交媒体的时间管理和沉迷问题?
在当今数字化时代,社交媒体已经成为了人们生活中不可或缺的一部分。然而,社交媒体的普及也带来了一个问题:时间管理和沉迷。本文将从多个角度对社交媒体的时间管理和沉迷问题进行分析,并探讨如何合理利用社交媒体并避免沉迷。
第…
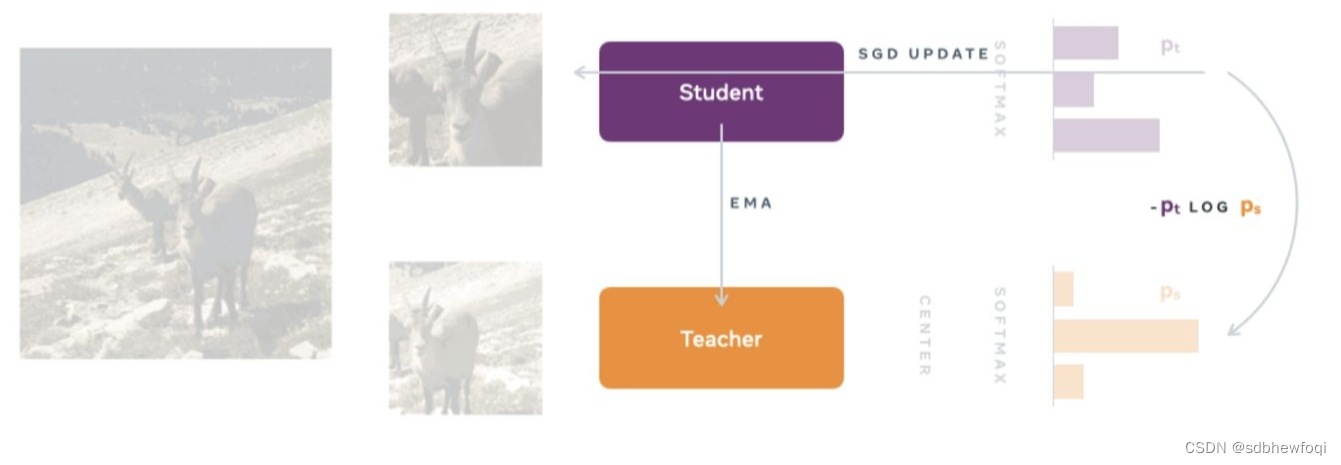
【计算机视觉】DINO
paper:Emerging Properties in Self-Supervised Vision Transformers
源码:https://github.com/facebookresearch/dino
20230627周二目前只把第一部分看完了。
论文导读:DINO -自监督视觉Transformers - deephub的文章 - 知乎、
DINO原理…
C生万物 | 细说动态内存管理【附经典笔试题】
文章目录 一、为什么存在动态内存分配二、动态内存函数的介绍1、malloc和free2、calloc3、reallocrealloc扩容机制:【本地扩容】和【异地扩容】实际应用:数据结构之【顺序表】与【顺序栈】 三、常见的动态内存错误1、对NULL指针的解引用操作2、对动态开辟…
Redisson源码-多线程之首个获取锁的线程加解锁流程
Redisson源码-多线程之首个获取锁的线程加解锁流程
简介 当有多个线程同时去获取同一把锁时,第一个获取到锁的线程会进行加解锁,其他线程需订阅消息并等待锁释放。
以下源码分析基于redisson-3.17.6版本,不同版本源码会有些许不同需注意。 …
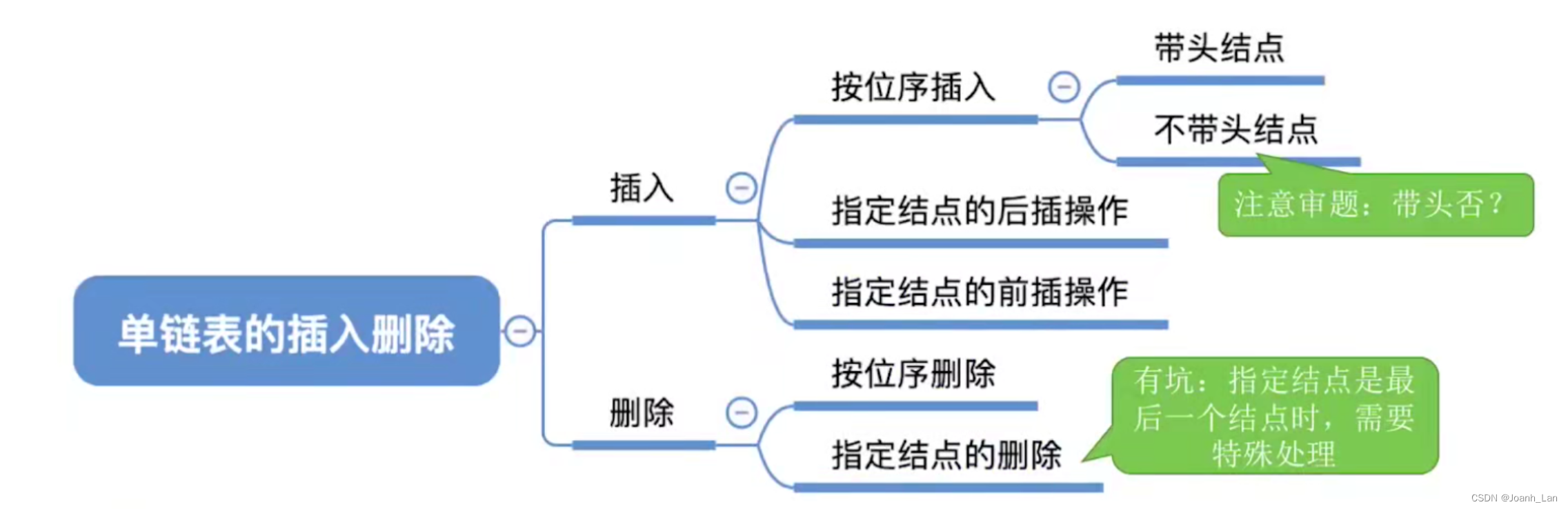
数据结构--单链表的插入删除
数据结构–单链表的插入&删除
目标 单链表的插入(位插、前插、后插) 单链表的删除
单链表的插入
按为序插入(带头结点)
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
思路:找到第i-1个结点,将新结点插入其…
软件工程期末报告(登录注册部分)
云小智微校园工具系统的设计与实现成员1注册模块
第一章 绪论
系统的背景描述和概述:可以描述系统服务的对象是学生,满足他们查询课程安排和上课时间的需求。目前市场上确实存在这方面的需求,这款app可以方便学生管理课程。系统采用客户端-服务器架构,运行在安卓平…
自学黑客(网络安全),一般人我劝你还是算了吧(自学网络安全学习路线--第十章 公钥基础设施-PKI)【建议收藏】
文章目录 一、自学网络安全学习的误区和陷阱二、学习网络安全的一些前期准备三、自学网络安全学习路线一、PKI概述1、理论基础2、PKI提供的安全服务 二、数字证书1、数字证书的格式2、数字证书的生命周期3、用JAVA工具生成数字证书 三、PKI组成四、PKI功能五、信任模型六、相关…
基于 Redis 手写一个“秒杀”
博主介绍: ✌博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家✌ Java知识图谱点击链接:体系化学习Java(Java面试专题) 💕💕 感兴趣的同学可以收…
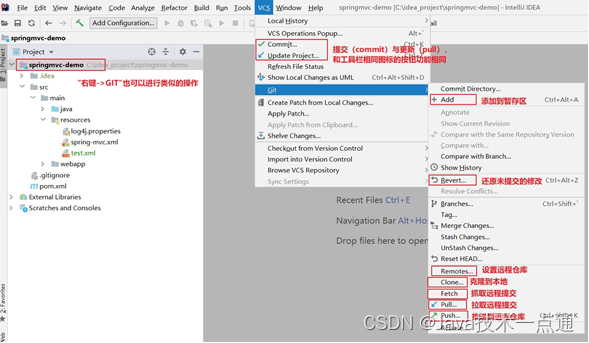
Git分布式版本控制工具 —— 详细笔记
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…
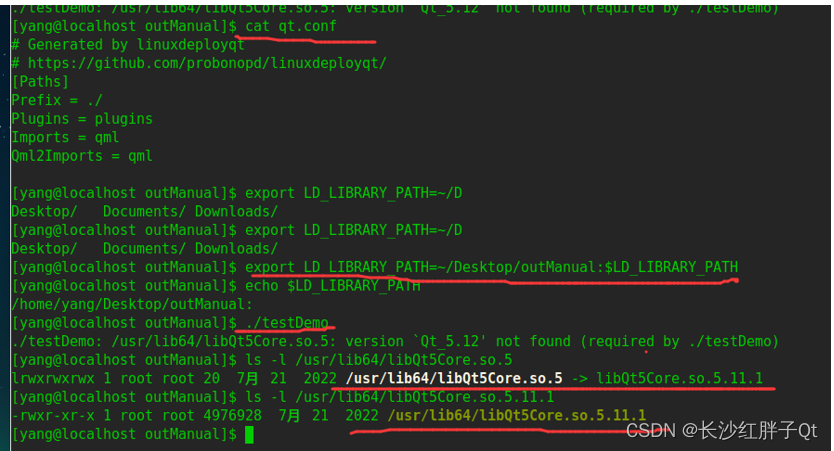
统信UOS系统开发笔记(七):在统信UOS系统上使用linuxdeployqt发布qt程序
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/131411975
红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软…
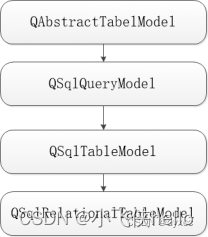
qt QSqlRelationalTableModel 详解
背景知识:
Qt SQL的API分为不同层:
驱动层 驱动层 对于QT是基于C来实现的框架,该层主要包括QSqlDriver、QSqlDriverCreator、QSqlDriverCreatorbase、QSqlDriverPlugin and QSqlResult。这一层提供了特定数据库和SQL API层之间的底层桥梁…
Problem I Rank LED题解 - 2018年第一届GXCPC广西大学生程序设计大赛 正式赛
Problem I Rank LED题解 题目大意
‘0’到‘9’的数字亮线依次为{6、2、5、5、4、5、6、3、7、6}。
Luras想修改每条光线的位置,使她的新等级尽可能小,同时新等级也是一个不带任何前导零的正整数。
另外,光线总数应与开始时相同。
官方题…
【AIGC】1、爆火的 AIGC 到底是什么 | 全面介绍
文章目录 一、AIGC 的简要介绍二、AIGC 的发展历程三、AIGC 的基石3.1 基本模型3.2 基于人类反馈的强化学习3.3 算力支持 四、生成式 AI(Generative AI)4.1 单模态4.1.1 生成式语言模型(Generative Language Models,GLM࿰…