总结

本系列为C++算法学习系列，会介绍 算法概念与描述，入门算法，基础算法，数值处理算法，排序算法，搜索算法，图论算法， 动态规划等相关内容。本文为搜索算法部分。

大纲要求

【 5 】深度优先搜索
【 5 】广度优先搜索

搜索算法-深度优先搜索

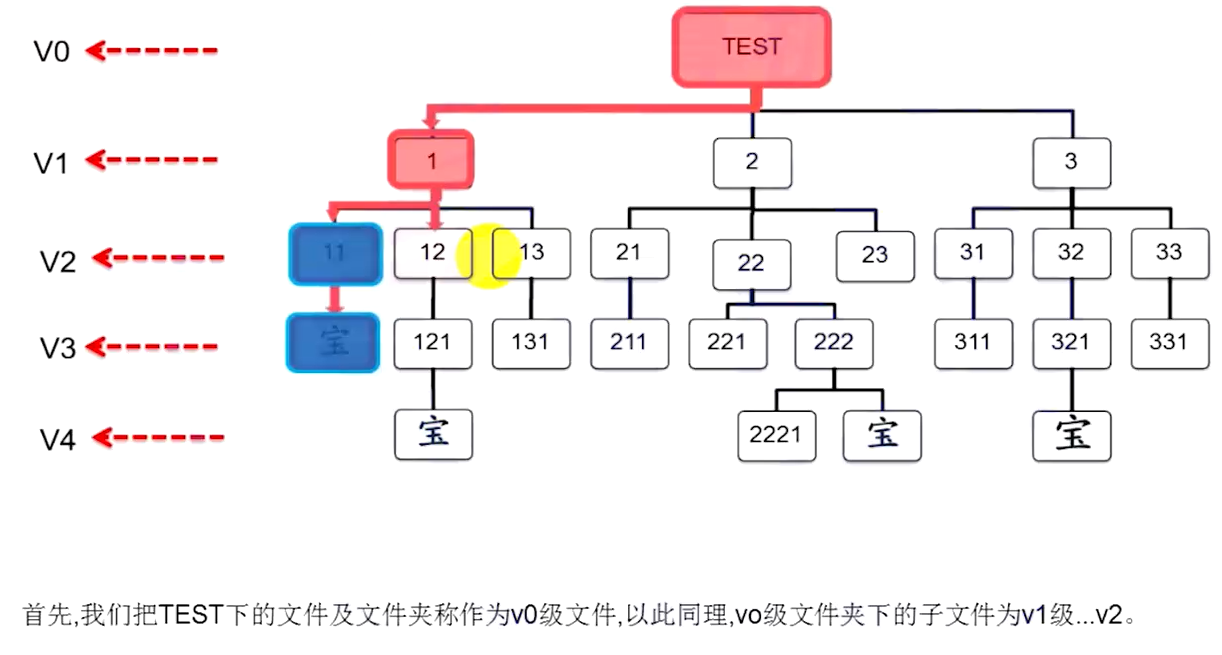
例1:全排列

现假设有n个整数，分别是1~n，现在将这n个数进行排列,每一个整数只能并且一定要出现一次，求它们的全排列。

每次选数的时候，都有n种可能，因为不能选重复的数，所以不一定所选的数都能成功的选上。
那么怎么办呢?我们不妨可以设置一个做标记的数组book[11]（我们经常使用的数组标记法），用作标记1-n你这n个数是否被选上的状态。
如果当前数字已经被选过，那么则选下一个数字。否则就选择当前数字，那下一步仍然用同样的方法进行筛选了! ! !
那显然我们首先想到的就是枚举，那么当n=10时，就是使用10个循环来枚举这10个数，当然是可以的，但这代码量…

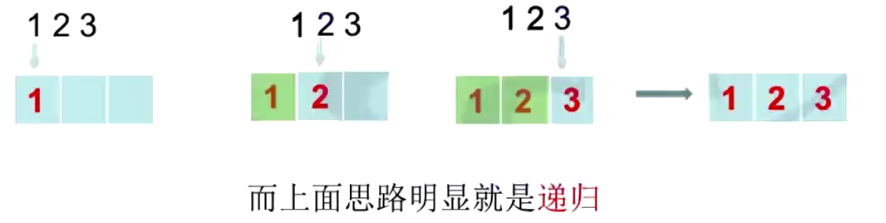
放置扑克牌的案例

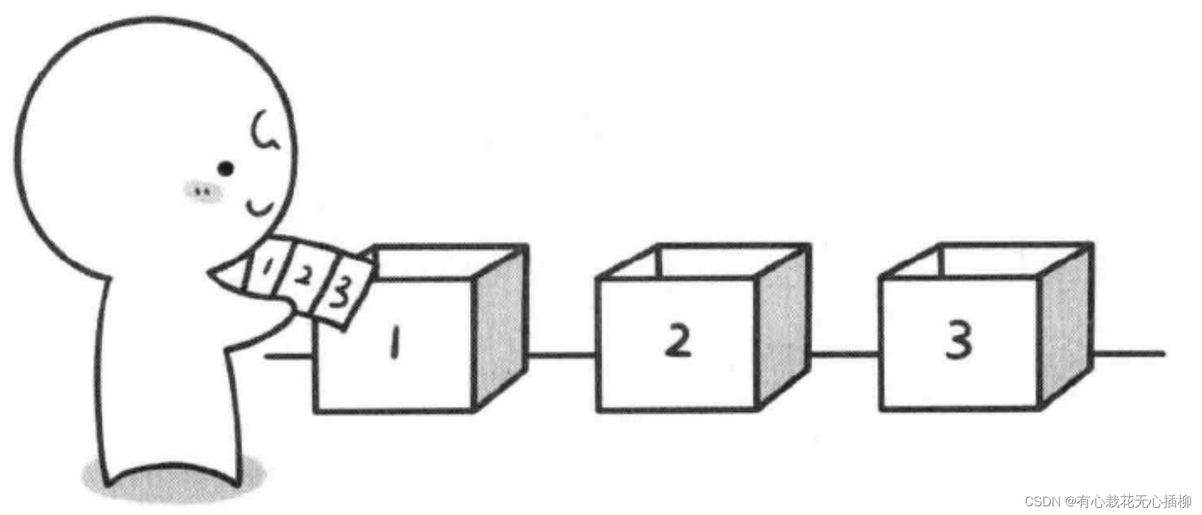
for(i = 1;i <= n;i++)
{
	a[step] = i;//将i号扑克牌放入到第step个盒子中
}

这里的数组a是用来表示小盒子的，变量step表示当前正处在第step个小盒子面前。a[step] = i;就是将第i号扑克牌，放入到第step个盒子中。
这里有一个问题就是，如果一张扑克牌已经放到别的小盒子中了，那么此时就不能再放入同样的扑克牌到别的盒子中了，因为此时手里已经没有扑克牌了。因此还需要一个数组book来标记哪些牌已经使用了。

for(i = 1;i <= n;i++)
{
	if(book[i] == false) //等于false，表示第i号牌没有被使用过 
	{
		a[step] = i;  //把i号牌放入到第step个盒子中
		book[i] = true;  //把book[i] 设为true,表示已经用过了i号牌
	}
}

我们现在已经处理完第step个小盒子了，接下来需要往下走一步，去处理第step+1个小盒子。
如何处理呢？
处理方法其实和我们刚刚处理第step个小盒子的方法相同。
把它封装成一个函数

void dfs(int step) // 表示站在第step个小盒子面前
{
	for(int i = 1; i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌是否用过
		{
			a[step] = i; //没用过就把第i号扑克牌放入第step个小盒子
			book[i] = true;//book[i]设为true，表示第i号扑克牌我们已经用过
		}
	}
}

把这个过程变成函数以后，就好处理第step + 1 个盒子了
就是 dfs(step + 1),来看代码

void dfs(int step) // 表示站在第step个小盒子面前
{
	for(int i = 1; i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌是否用过
		{
			a[step] = i; //没用过就把第i号扑克牌放入第step个小盒子
			book[i] = true;//book[i]设为true，表示第i号扑克牌我们已经用过


			dfs(step + 1);//通过函数递归来实现（函数自己调用自己）
			book[i] = false;
//这里是非常重要的一步，一定要将刚才尝试的扑克牌收回，才能进行下一次尝试
		}
	}
}

book[i] = false;
这一步非常重要，也就是我们上面说的回溯，回溯要恢复到原来的场景。
也就是我们把扑克牌收回，否则无法进行下一次的摆放。
现在还有一个问题，就是什么时候输出一个满足要求的序列呢？
其实当我们处理第n + 1个小盒子的时候（即step = n + 1），说明前n个小盒子已经放好扑克牌了，这里将1~n个小盒子中的扑克牌编号打印出来就可以了。注意！打印完毕之后一定要return，否则程序就会永无止境地进行下去了，也就是要有递归的终止条件。

void dfs(int step) // step 表示现在站在第几个盒子面前
{
	if(step == n + 1) //如果站在第n+1个盒子面前，则表示前n个盒子已经放好扑克牌
	{
	//输出一种排列，即 1 ~ n 号盒子中扑克牌编号
		for(int i = 1;i <= n;i++)
		{
			printf("%d ",a[i]);
		}
		printf("\n");
		return; // 返回之前的一步（最近一次调用dfs的地方）
	}
	for(int i = 1;i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌i是否已经用过
		{
			a[step] = i; //如果没用过，就把i号牌放在第step个盒子
			book[i] = true;//i号牌记录为已经用过
			dfs(step + 1);//处理第step+1个盒子，函数递归实现
			book[i] = false;//将刚才的扑克牌收回，才能进行下一次尝试
		}
	}
}

#include <iostream>
using namespace std;

//int a[N];//开辟的盒子
int a[11],book[11],n,sum=0;
// 把n个扑克牌放在n个盒子中
void dfs(int t) //t表示现在站在第几个盒子面前
{
    if(t==n+1) //如果站在第n+1个盒子面前，则表示前n个盒子已经放好扑克牌
    {
        sum++;
        //输出一种排列，即 1 ~ n 号盒子中扑克牌编号
        for(int i=1;i<=n;i++)
        {
            cout<<a[i];
        }
        cout<<endl;
        return; //返回之前的一步（最近一次调用dfs的地方）
    }
    for(int i=1;i<=n;i++)
    {
        if(book[i]==0) //判断扑克牌i是否已经用过
        {
            a[t]=i;//选择该数，保存 //如果没用过，就把i号牌放在第step个盒子
            book[i]=1; //i号牌记录为已经用过
            dfs(t+1);//下一步筛选 //处理第step+1个盒子，函数递归实现
            book[i]=0;// 回溯到上一部的状态 将刚才的扑克牌收回，才能进行下一次尝试
        }

    }

}

int main()
{
    cin>>n;
    dfs(1);
    cout<<sum;
	return 0;
}

n皇后案例

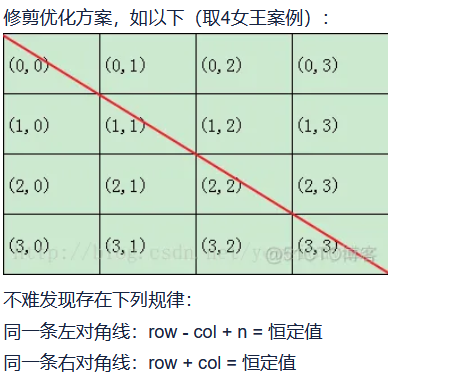
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

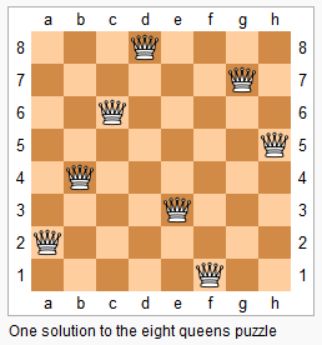
现在给定整数 n，请你输出所有的满足条件的棋子摆法。
输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后，输出一个空行。
注意：行末不能有多余空格。
输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

#include<iostream>

using namespace std;

const int N = 20;//对角线的个数是2n - 1
char g[N][N];//存储当前的图
bool col[N], dg[N], udg[N];//列和对角线以及反对角线是否有皇后（true 有，false无）

int n;

void dfs(int u)
{
	if(u == n)//表示已经搜了n行，故输出这条路径
	{
		for(int i = 0; i < n; i ++)puts(g[i]);
		puts("");//puts输出字符串
		return;
	}

	for(int i = 0; i < n; i ++)
	{
		if(!col[i] && !dg[u + i] && !udg[n - u + i])//对角线为 n- u + i, 反对角线下标为 u + i
		{
			g[u][i] = 'Q';
			col[i] = dg[u + i] = udg[n - u + i] = true;

			dfs(u + 1);
			//还原现场
			col[i] = dg[u + i] = udg[n - u + i] = false;
			g[u][i] = '.';
		}
	}
}


int main()
{
	cin >> n; // 几个皇后

	for(int i = 0; i < n; i ++)
		for(int j = 0; j < n; j ++)
			g[i][j] = '.';

	dfs(0);

	return 0;
}
//dfs与递归类似

搜索算法-广度优先搜索

在深度优先搜索算法中，是深度越大的结点越先得到扩展。如果在搜索中把算法改为按结点的层次进行搜索，本层的结点没有搜索处理完时，不能对下层结点进行处理，即深度越小的结点越先得到扩展，也就是说先产生的结点先得以扩展处理，这种搜索算法称为广度优先搜索法。