(本文内容为个人笔记分享)
牛顿二项公式
( x + y ) n = ∑ k = 0 n C n k ⋅ x n − k y k (x+y)^n=\stackrel{n}{\sum\limits_{k=0}}C^k_n\sdot x^{n-k}y^k (x+y)n=k=0∑nCnk⋅xn−kyk.
映射
f : X → Y f:X\rightarrow Y f:X→Y, f f f 为 X X X 到 Y Y Y 的映射。 f f f 是一个对应关系, X , Y X,Y X,Y 是两个非空集合。在对应关系 f f f 下, X X X 中的元素 x x x 在 Y Y Y 中有唯一确定的元素 y y y 与之对应。
- y y y 为 x x x 在 f f f 下的像。
- x x x 为 y y y 在 f f f 下的原像。
集合 X X X 是 映射 f f f 的定义域,记 D f D_f Df,即 D f = X D_f=X Df=X.
X X X 中所有元素的 像 组成的 集合 称为 映射 f f f 的 值域,记 R f R_f Rf 或 f ( X ) f(X) f(X),即 R f = f ( X ) = { f ( x ) ∣ x ∈ X } R_f=f(X)=\{f(x)|x\in X\} Rf=f(X)={f(x)∣x∈X}.
- 对于每一个元素 x ∈ X x\in X x∈X,在 Y Y Y 中的像 y y y 是唯一的。但对于每一个元素 y ∈ Y y\in Y y∈Y,在 X X X 中的原像不一定是唯一的。
- R f ⊂ Y R_f\subset Y Rf⊂Y,不一定 R f = Y R_f=Y Rf=Y.
对于 f : X → Y f:X\rightarrow Y f:X→Y,
- 若 R f = Y R_f=Y Rf=Y,则称 f : X → Y f:X\rightarrow Y f:X→Y 为 满射。(集合 Y Y Y 中每个元素在集合 X X X 中都能找到它的原像。)
- 若 x 1 ≠ x 2 , ( x 1 , x 2 ∈ X ) x_1\neq x_2,(x_1,x_2\in X) x1=x2,(x1,x2∈X) 且 f ( x 1 ) ≠ f ( x 2 ) f(x_1)\neq f(x_2) f(x1)=f(x2),则称 f : X → Y f:X\rightarrow Y f:X→Y 为 单射。(集合 X X X 中任意两个元素在 Y Y Y 中的像不相等, X X X 中任意两个元素的像没有重复。)
- 既是满射又是单射的映射称为一一映射或双射。
映射又称算子。在不同数学分支有着不同的惯用名,非空集 X X X 到 数集 Y Y Y 的映射称为 X X X 上的 泛函;从非空集 X X X 到它自身的映射又称为 X X X 上的 变换;从 实数集 R R R(或其子集) 到实数集 Y Y Y 的映射通常称为 定义在 X X X 上的 函数。
逆映射与复合映射:
f : X → Y f:X\rightarrow Y f:X→Y 是单射,则其存在逆映射。
f : X → Y f:X\rightarrow Y f:X→Y 是单射,则 y ∈ R f y\in R_f y∈Rf,有唯一的 x ∈ X x\in X x∈X, f ( x ) = y f(x)=y f(x)=y.
定义一个新的映射 g : R f → X g:R_f\rightarrow X g:Rf→X,每个 y ∈ R f y\in R_f y∈Rf, g ( y ) = x g(y)=x g(y)=x.
g g g 为 f f f 的 逆映射。记 g = f − 1 g=f^{-1} g=f−1, g g g 的定义域 D g = D f − 1 = R f Dg=D_{f^{-1}}=R_f Dg=Df−1=Rf, g g g 的值域 R g = R f − 1 = X R_g=R_{f^{-1}}=X Rg=Rf−1=X.
f : [ − π 2 , π 2 ] → [ − 1 , 1 ] f:[-\dfrac{\pi}{2},\dfrac{\pi}{2}]\rightarrow [-1,1] f:[−2π,2π]→[−1,1],对每个 x ∈ [ − π 2 , π 2 ] x\in [-\dfrac{\pi}{2},\dfrac{\pi}{2}] x∈[−2π,2π], f ( x ) = sin x f(x)=\sin x f(x)=sinx 是一个映射,定义域 D f = [ − π 2 , π 2 ] D_f=[-\dfrac{\pi}{2},\dfrac{\pi}{2}] Df=[−2π,2π],值域 R f = [ − 1 , 1 ] R_f=[-1,1] Rf=[−1,1]. 此时, f f f 是一个单射,所以其存在逆映射 f − 1 = arcsin x , x ∈ [ − 1 , 1 ] f^{-1}=\arcsin x,\ x\in [-1,1] f−1=arcsinx, x∈[−1,1], f − 1 f^{-1} f−1 就是反正弦函数,定义域 D f − 1 = [ − 1 , 1 ] D_{f^{-1}}=[-1,1] Df−1=[−1,1],值域 R f − 1 = [ − π 2 , π 2 ] R_{f^{-1}}=[-\dfrac{\pi}{2},\dfrac{\pi}{2}] Rf−1=[−2π,2π].
两个映射 g : X → Y 1 g:X\rightarrow Y_1 g:X→Y1 和 f : Y 2 → Z f:Y_2\rightarrow Z f:Y2→Z,
Y 1 ⊂ Y 2 Y_1\subset Y_2 Y1⊂Y2,则可以定义复合映射:
f ∘ g : X → Z , ( f ∘ g ) ( x ) = f [ g ( x ) ] , x ∈ X f\circ g:X\rightarrow Z,\ (f\circ g)(x)=f[g(x)],\ x\in X f∘g:X→Z, (f∘g)(x)=f[g(x)], x∈X.
- 满足条件: R g ⊂ D f R_g\subset D_f Rg⊂Df.
- f ∘ g f\circ g f∘g 有意义并不代表 g ∘ f g\circ f g∘f 有意义.
- f ∘ g f\circ g f∘g 和 g ∘ f g\circ f g∘f 都有意义,符合映射 f ∘ g f\circ g f∘g 与 g ∘ f g\circ f g∘f 也未必相同.
映射 g : R → [ − 1 , 1 ] g:\mathrm{R}\rightarrow[-1,1] g:R→[−1,1],对每个 x ∈ R x\in\mathrm{R} x∈R, g ( x ) = sin x g(x)=\sin x g(x)=sinx;映射 f : [ − 1 , 1 ] → [ 0 , 1 ] f:[-1,1]\rightarrow[0,1] f:[−1,1]→[0,1],对每个 u ∈ [ − 1 , 1 ] u\in[-1,1] u∈[−1,1], f ( u ) = 1 − u 2 f(u)=\sqrt{1-u^2} f(u)=1−u2,
复合映射 f ∘ g : R → [ 0 , 1 ] f\circ g:\mathrm{R}\rightarrow[0,1] f∘g:R→[0,1],对每个 x ∈ R x\in\mathrm{R} x∈R,有 ( f ∘ g ) ( x ) = f [ g ( x ) ] = f ( sin x ) = 1 − sin 2 x = ∣ cos x ∣ (f\circ g)(x)=f[g(x)]=f(\sin x)=\sqrt{1-\sin^2x}=|\cos x| (f∘g)(x)=f[g(x)]=f(sinx)=1−sin2x=∣cosx∣.
函数
定义:设数集 D ⊂ R D\subset\mathrm{R} D⊂R,则称映射 f : D → R f:D\rightarrow\mathrm{R} f:D→R 为定义在 D D D 上的函数,通常记为 y = f ( x ) , x ∈ D y=f(x),\ x\in D y=f(x), x∈D。
- x x x 自变量
- y y y 因变量
- D D D 定义域,记 D f D_f Df.
x x x 处的函数值 y = f ( x ) y=f(x) y=f(x). x x x 与 y y y 的函数关系。全体函数值 f ( x ) f(x) f(x) 构成的集合称为值域 R f R_f Rf 或 f ( D ) f(D) f(D). R f = f ( D ) = { y ∣ y = f ( x ) , x ∈ D } R_f=f(D)=\{y|y=f(x),x\in D\} Rf=f(D)={y∣y=f(x),x∈D}.
符号函数: y = s g n x = { − 1 , x < 0 , 0 , x = 0 , 1 , x > 0. y=\mathrm{sgn}\ x=\begin{cases}-1,&x<0,\\0,&x=0,\\1,&x>0.\end{cases} y=sgn x=⎩ ⎨ ⎧−1,0,1,x<0,x=0,x>0.
x = s g n x ⋅ x x=\mathrm{sgn}\ x\cdot x x=sgn x⋅x.
取整函数: y = [ x ] y=[x] y=[x],图像为阶梯曲线,定义域 D = ( − ∞ , + ∞ ) D=(-\infty,+\infty) D=(−∞,+∞),值域 R f = Z R_f=\mathrm{Z} Rf=Z.
函数的特性
- 有界性:
- f ( x ) ≤ K 1 f(x)\leq K_1 f(x)≤K1, K 1 K_1 K1 为 f ( x ) f(x) f(x) 在 X X X 上的一个 上界
- f ( x ) ≥ K 2 f(x)\geq K_2 f(x)≥K2, K 2 K_2 K2 为 f ( x ) f(x) f(x) 在 X X X 上的一个 下界
- ∣ f ( x ) ∣ ≤ M |f(x)|\leq M ∣f(x)∣≤M, f ( x ) f(x) f(x) 在 X X X 上 有界
- ∀ M ∈ R + , ∃ x 1 ∈ X , ∣ f ( x 1 ) ∣ > M \forall M\in\mathrm{R}^+,\exist x_1\in X,|f(x_1)|>M ∀M∈R+,∃x1∈X,∣f(x1)∣>M,则 f ( x ) f(x) f(x) 在 X X X 上无界。
- 若 f ( x ) f(x) f(x) 在 X X X 上既有上界又有下届,则 f ( x ) f(x) f(x) 在 X X X 上有界。
- 单调性:
- f ( x ) f(x) f(x), I ⊂ D I\subset D I⊂D, ∀ x 1 , x 2 ∈ I , x 1 < x 2 \forall x_1,x_2\in I,\ x_1<x_2 ∀x1,x2∈I, x1<x2,有 f ( x 1 ) < f ( x 2 ) f(x_1)<f(x_2) f(x1)<f(x2),则 f ( x ) f(x) f(x) 在区间 I I I 上是 单调增加 的。
- f ( x ) f(x) f(x), I ⊂ D I\subset D I⊂D, ∀ x 1 , x 2 ∈ I , x 1 < x 2 \forall x_1,x_2\in I,\ x_1<x_2 ∀x1,x2∈I, x1<x2,有 f ( x 1 ) > f ( x 2 ) f(x_1)>f(x_2) f(x1)>f(x2),则 f ( x ) f(x) f(x) 在区间 I I I 上是 单调减少 的。
- 单调增加和单调减少的函数统称为 单调函数。
函数的奇偶性:
- f ( x ) = f ( − x ) f(x)=f(-x) f(x)=f(−x),关于 x = 0 x=0 x=0 对称,偶函数。
- f ( x ) = − f ( − x ) f(x)=-f(-x) f(x)=−f(−x),关于 ( 0 , 0 ) (0,0) (0,0) 对称,奇函数。
函数的周期性:
f ( x ) f(x) f(x) 定义域 D D D, ∃ l ∈ R + \exist l\in \mathrm{R}^+ ∃l∈R+,使 ∀ x ∈ D \forall x\in D ∀x∈D 有 ( x ± l ) ∈ D (x\pm l)\in D (x±l)∈D,且 f ( x + l ) = f ( x ) f(x+l)=f(x) f(x+l)=f(x). 则称 f ( x ) f(x) f(x) 为周期函数, l l l 称为 f ( x ) f(x) f(x) 的周期,(最小正周期)。
y = sin x y=\sin x y=sinx :(奇函数,周期 2 π 2\pi 2π.)
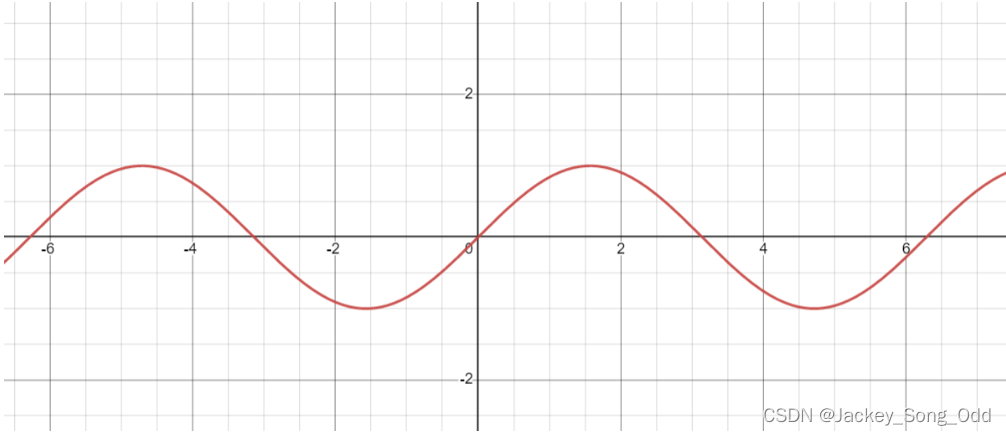
y = cos x y=\cos x y=cosx :(偶函数,周期 2 π 2\pi 2π.)
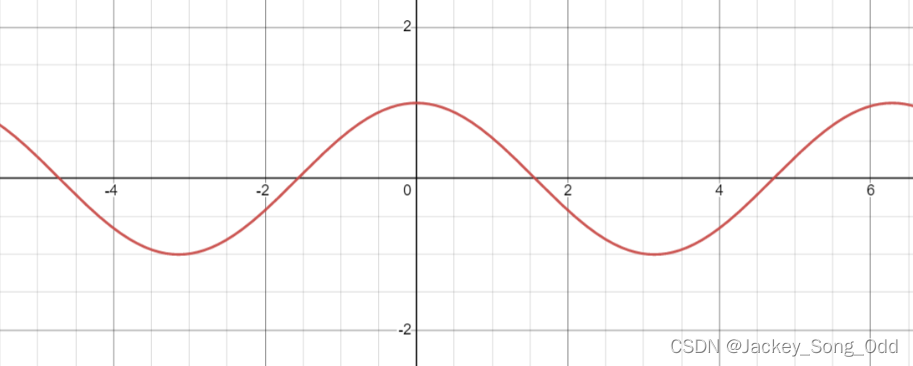
y = sin ( x + π 4 ) y=\sin(x+\dfrac{\pi}{4}) y=sin(x+4π):
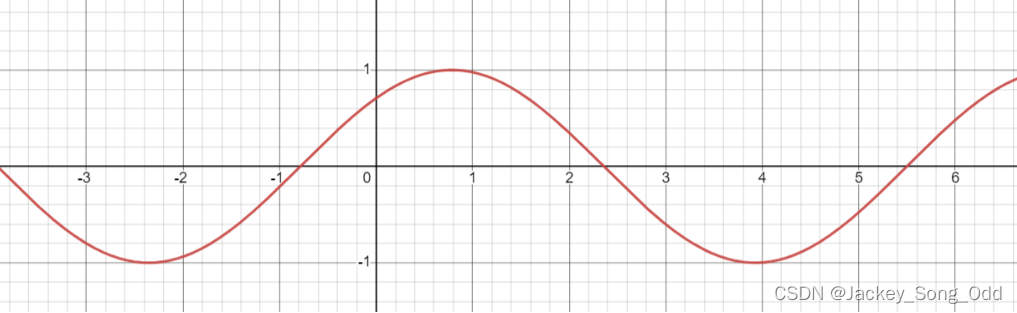
y = sin x + cos x y=\sin x + \cos x y=sinx+cosx :(非奇非偶函数,周期 2 π 2\pi 2π.)
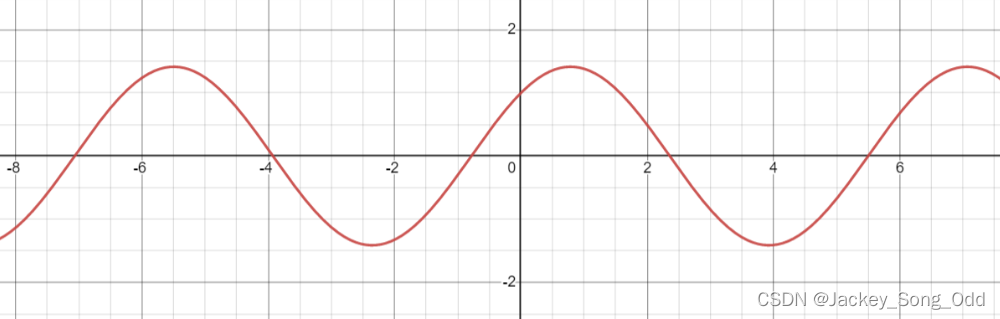
y = sin x + cos x = 2 ( sin x ⋅ 2 2 + cos x ⋅ 2 2 ) y=\sin x+\cos x=\sqrt{2}(\sin x\cdot\dfrac{\sqrt{2}}{2}+\cos x\cdot\dfrac{\sqrt{2}}{2}) y=sinx+cosx=2(sinx⋅22+cosx⋅22)
= 2 ( sin x ⋅ cos π 4 + cos x ⋅ sin π 4 ) =\sqrt{2}(\sin x\cdot\cos\dfrac{\pi}{4}+\cos x\cdot\sin\dfrac{\pi}{4}) =2(sinx⋅cos4π+cosx⋅sin4π)
= 2 sin ( x + π 4 ) =\sqrt{2}\sin(x+\dfrac{\pi}{4}) =2sin(x+4π).
y = 2 sin ( x + π 4 ) y=\sqrt{2}\sin(x+\dfrac{\pi}{4}) y=2sin(x+4π) 由 y = sin x y=\sin x y=sinx 左移了 π 4 \dfrac{\pi}{4} 4π 单位再整体乘以 2 \sqrt{2} 2 得来。
y = tan x y=\tan x y=tanx :(奇函数,周期 π \pi π.)
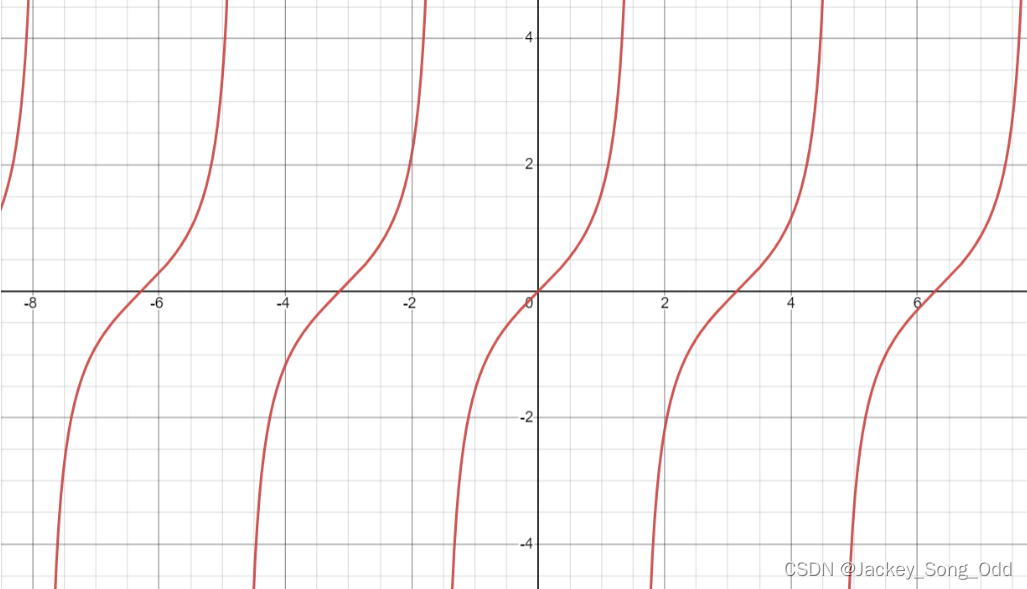
Dirichlet 狄利克雷函数:
D ( x ) = { 1 , x ∈ Q , 0 , x ∈ Q C . D(x)=\begin{cases}1,&x\in\mathrm{Q},\\0,&x\in\mathrm{Q}^C.\end{cases} D(x)={1,0,x∈Q,x∈QC.
Q C \mathrm{Q}^C QC,角标 C C C 一般表示有理数集 Q \mathrm{Q} Q 相对于实数集 R \mathrm{R} R 的补集, Q C \mathrm{Q}^C QC 的意思就是 无理数集。
任何有理数加上一个有理数,还是有理数;任何无理数加上一个有理数,还是一个无理数。对于这个函数,任何有理数都是它的周期。
∵ \because ∵ 没有最小的有理数
∴ \therefore ∴ Dirichlet 函数没有最小正周期。
反函数与复合函数
反:
设函数 f : D → f ( D ) f:D\rightarrow f(D) f:D→f(D) 是单射,则它存在逆映射 f − 1 : f ( D ) → D f^{-1}:f(D)\rightarrow D f−1:f(D)→D,则称此映射 f − 1 f^{-1} f−1 为函数 f f f 的反函数。
一般地, y = f ( x ) y=f(x) y=f(x), x ∈ D x\in D x∈D 的反函数记成 y = f − 1 ( x ) , x ∈ f ( D ) y=f^{-1}(x), x\in f(D) y=f−1(x),x∈f(D).
相对于反函数 y = f − 1 ( x ) y=f^{-1}(x) y=f−1(x) 来说,原来的函数 y = f ( x ) y=f(x) y=f(x) 称为 直接函数,它俩在函数图像上关于直线 y = x y=x y=x 对称,其实 y = f − 1 ( x ) y=f^{-1}(x) y=f−1(x) 就是由 y = f ( x ) y=f(x) y=f(x) 对换 x x x 轴 和 y y y 轴 得到的函数图像。
复合:
y = f ( u ) y=f(u) y=f(u) 定义域 D f D_f Df, u = g ( x ) u=g(x) u=g(x) 定义域 D g D_g Dg,其值域 R g ⊂ D f R_g\subset D_f Rg⊂Df,则确定一个 复合函数 : y = f [ g ( x ) ] , x ∈ D g y=f[g(x)],\quad x\in D_g y=f[g(x)],x∈Dg. u u u 为 中间变量。
先 g g g 后 f f f 的复合,记为 f ∘ g f\circ g f∘g,即: ( f ∘ g ) ( x ) = f [ g ( x ) ] (f\circ g)(x)=f[g(x)] (f∘g)(x)=f[g(x)].
f ( x ) , g ( x ) f(x),g(x) f(x),g(x) 的定义域为 D f , D g D_f,D_g Df,Dg, D = D f ∩ D g ≠ ∅ D=D_f\cap D_g\neq\empty D=Df∩Dg=∅,定义两个函数的运算:
- 和(差): ( f ± g ) ( x ) = f ( x ) ± g ( x ) , x ∈ D ; (f\pm g)(x)=f(x)\pm g(x),\quad x\in D; (f±g)(x)=f(x)±g(x),x∈D;
- 积: ( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) , x ∈ D ; (f\cdot g)(x)=f(x)\cdot g(x),\quad x\in D; (f⋅g)(x)=f(x)⋅g(x),x∈D;
- 商: ( f g ) ( x ) = f ( x ) g ( x ) , x ∈ D − { x ∣ g ( x ) = 0 , x ∈ D } \Big(\dfrac{f}{g}\Big)(x)=\dfrac{f(x)}{g(x)},\quad x\in D-\{x|g(x)=0,x\in D\} (gf)(x)=g(x)f(x),x∈D−{x∣g(x)=0,x∈D}.
任何定义在 ( − l , l ) (-l,l) (−l,l) 上的函数 f ( x ) f(x) f(x) 都可以写成 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x) 的形式,其中 g ( x ) g(x) g(x) 为 ( − l , l ) (-l,l) (−l,l) 上的偶函数, h ( x ) h(x) h(x) 为 ( − l , l ) (-l,l) (−l,l) 上的奇函数。
设函数 f ( x ) f(x) f(x) 的定义域为 ( − l , l ) (-l,l) (−l,l),证明必存在 ( − l , l ) (-l,l) (−l,l) 上的偶函数 g ( x ) g(x) g(x) 及奇函数 h ( x ) h(x) h(x),使得 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x).
证明:
假设存在这种的 g ( x ) g(x) g(x) 和 h ( x ) h(x) h(x),使得 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x).
且 g ( x ) = g ( − x ) g(x)=g(-x) g(x)=g(−x), h ( − x ) = − h ( x ) h(-x)=-h(x) h(−x)=−h(x).
则 f ( − x ) = g ( − x ) + h ( − x ) = g ( x ) − h ( x ) f(-x)=g(-x)+h(-x)=g(x)-h(x) f(−x)=g(−x)+h(−x)=g(x)−h(x).
g ( x ) = 1 2 [ f ( x ) + f ( − x ) ] g(x)=\dfrac{1}{2}[f(x)+f(-x)] g(x)=21[f(x)+f(−x)].
h ( x ) = 1 2 [ f ( x ) − f ( − x ) ] h(x)=\dfrac{1}{2}[f(x)-f(-x)] h(x)=21[f(x)−f(−x)].
g ( x ) + h ( x ) = f ( x ) g(x)+h(x)=f(x) g(x)+h(x)=f(x).
g ( − x ) = 1 2 [ f ( − x ) + f ( x ) ] = g ( x ) g(-x)=\dfrac{1}{2}[f(-x)+f(x)]=g(x) g(−x)=21[f(−x)+f(x)]=g(x).
h ( − x ) = 1 2 [ f ( − x ) − f ( x ) ] = − h ( x ) h(-x)=\dfrac{1}{2}[f(-x)-f(x)]=-h(x) h(−x)=21[f(−x)−f(x)]=−h(x).
由结论 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x) 反推条件 g ( x ) = g ( − x ) g(x)=g(-x) g(x)=g(−x), h ( − x ) = − h ( x ) h(-x)=-h(x) h(−x)=−h(x).
当 f ( x ) f(x) f(x) 是偶函数时, h ( x ) = 0 h(x)=0 h(x)=0,它既是关于 x = 0 x=0 x=0 对称的偶函数,也是关于 ( 0 , 0 ) (0,0) (0,0) 对称的奇函数。
初等函数
- 幂函数: y = x μ y=x^{\mu} y=xμ,( μ ∈ R \mu\in\mathrm{R} μ∈R 是常数)
- 指数函数: y = a x y=a^x y=ax,( a > 0 a>0 a>0, a ≠ 1 a\neq1 a=1)
- 对数函数: y = log a x y=\log_ax y=logax,( a > 0 a>0 a>0 且 a ≠ 1 a\neq1 a=1,特别当 a = e a=e a=e 时,记为 y = ln x y=\ln x y=lnx, e ≈ 2.718 e\approx2.718 e≈2.718,是一个无理数。)
- 三角函数: y = sin x , y = cos x , y = tan x y=\sin x,y=\cos x,y=\tan x y=sinx,y=cosx,y=tanx 等
- 反三角函数: y = arcsin x , y = arccos x , y = arctan x y=\arcsin x,y=\arccos x,y=\arctan x y=arcsinx,y=arccosx,y=arctanx 等
以上这五类为 基本初等函数。
由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数,称为初等函数,例如:
y = 1 − x 2 , y = sin 2 x , y = cot x 2 y=\sqrt{1-x^2},\quad y=\sin^2x,\quad y=\sqrt{\cot\dfrac{x}{2}} y=1−x2,y=sin2x,y=cot2x
双曲正弦
y = s h x = e x − e − x 2 y=\mathrm{sh}\ x=\dfrac{e^x-e^{-x}}{2} y=sh x=2ex−e−x
双曲余弦
y = c h x = e x + e − x x y=\mathrm{ch}\ x=\dfrac{e^x+e^{-x}}{x} y=ch x=xex+e−x
双曲正切
y = t h x = e x − e − x e x + e − x y=\mathrm{th}\ x=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} y=th x=ex+e−xex−e−x

公式
- s h ( x ± y ) = s h x ⋅ c h y ± c h x ⋅ s h y \mathrm{sh}\ (x\pm y)=\mathrm{sh}\ x\cdot\mathrm{ch}\ y\pm\mathrm{ch}\ x\cdot\mathrm{sh}\ y sh (x±y)=sh x⋅ch y±ch x⋅sh y
- c h ( x ± y ) = c h x ⋅ c h y ± s h x ⋅ s h y \mathrm{ch}\ (x\pm y)=\mathrm{ch}\ x\cdot\mathrm{ch}\ y\pm\mathrm{sh}\ x\cdot\mathrm{sh}\ y ch (x±y)=ch x⋅ch y±sh x⋅sh y
对于 c h ( x − y ) = c h x ⋅ c h y − s h x ⋅ s h y \mathrm{ch}\ (x-y)=\mathrm{ch}\ x\cdot\mathrm{ch}\ y-\mathrm{sh}\ x\cdot\mathrm{sh}\ y ch (x−y)=ch x⋅ch y−sh x⋅sh y,当 x = y x=y x=y 时,有 c h ( x − x ) = c h 0 = c h 2 x − s h 2 x = 1 \mathrm{ch}\ (x-x)=\mathrm{ch}\ 0=\mathrm{ch}^2\ x-\mathrm{sh}^2\ x=1 ch (x−x)=ch 0=ch2 x−sh2 x=1.
对于 s h ( x + y ) = s h x ⋅ c h y + c h x ⋅ s h y \mathrm{sh}\ (x+y)=\mathrm{sh}\ x\cdot\mathrm{ch}\ y+\mathrm{ch}\ x\cdot\mathrm{sh}\ y sh (x+y)=sh x⋅ch y+ch x⋅sh y,当 x = y x=y x=y 时,有 s h 2 x = 2 c h x ⋅ s h x \mathrm{sh}\ 2x=2\mathrm{ch}\ x\cdot\mathrm{sh}\ x sh 2x=2ch x⋅sh x.
对于 c h ( x + y ) = c h x ⋅ c h y + s h x ⋅ s h y \mathrm{ch}\ (x+y)=\mathrm{ch}\ x\cdot\mathrm{ch}\ y+\mathrm{sh}\ x\cdot\mathrm{sh}\ y ch (x+y)=ch x⋅ch y+sh x⋅sh y,当 x = y x=y x=y 时,有 c h 2 x = c h 2 x + s h 2 x \mathrm{ch}\ 2x=\mathrm{ch}^2 x+\mathrm{sh}^2 x ch 2x=ch2x+sh2x.
双曲函数 y = s h x , y = c h x ( x ≥ 0 ) , y = t h x y=\mathrm{sh}\ x,y=\mathrm{ch}\ x\quad (x\geq0),y=\mathrm{th}\ x y=sh x,y=ch x(x≥0),y=th x 的反函数依次记为:
反双曲正弦: y = a r s h x y=\mathrm{arsh}\ x y=arsh x
反双曲余弦: y = a r c h x y=\mathrm{arch}\ x y=arch x
反双曲正切: y = a r t h x y=\mathrm{arth}\ x y=arth x
y = s h x y=\mathrm{sh}\ x y=sh x 的反函数: y = a r s h x = ln ( x + x 2 + 1 ) y=\mathrm{arsh}\ x=\ln(x+\sqrt{x^2+1}) y=arsh x=ln(x+x2+1). 推导过程如下:
x = s h y = e y − e − y 2 x=\mathrm{sh}\ y=\dfrac{e^y-e^{-y}}{2} x=sh y=2ey−e−y
令 u = e y u=e^y u=ey
x = u − 1 u 2 x=\dfrac{u-\dfrac{1}{u}}{2} x=2u−u1
u 2 − 2 x u − 1 = 0 u^2-2xu-1=0 u2−2xu−1=0
u = 2 x ± 4 x 2 + 4 2 = x ± x 2 + 1 u=\dfrac{2x\pm\sqrt{4x^2+4}}{2}=x\pm\sqrt{x^2+1} u=22x±4x2+4=x±x2+1
∵ u = e y > 0 \because u=e^y>0 ∵u=ey>0
又 ∵ x 2 + 1 > x \because \sqrt{x^2+1}>x ∵x2+1>x
∴ \therefore ∴ 只能取正号: u = x + x 2 + 1 u=x+\sqrt{x^2+1} u=x+x2+1
y = a r s h x = ln ( x + x 2 + 1 ) y=\mathrm{arsh}\ x=\ln(x+\sqrt{x^2+1}) y=arsh x=ln(x+x2+1), x + x 2 + 1 > 0 x+\sqrt{x^2+1}>0 x+x2+1>0,即 x ∈ ( − ∞ , + ∞ ) x\in (-\infty,+\infty) x∈(−∞,+∞).
− y = − f ( x ) = − ln ( x + x 2 + 1 ) = ln 1 x + x 2 + 1 = ln − x + x 2 + 1 ( x 2 + 1 + x ) ( x 2 + 1 − x ) = ln − x + x 2 + 1 ( x 2 + 1 ) − x 2 = ln ( − x + x 2 + 1 ) -y=-f(x)=-\ln(x+\sqrt{x^2+1})=\ln\dfrac{1}{x+\sqrt{x^2+1}}=\ln\dfrac{-x+\sqrt{x^2+1}}{(\sqrt{x^2+1}+x)(\sqrt{x^2+1}-x)}=\ln\dfrac{-x+\sqrt{x^2+1}}{(x^2+1)-x^2}=\ln(-x+\sqrt{x^2+1}) −y=−f(x)=−ln(x+x2+1)=lnx+x2+11=ln(x2+1+x)(x2+1−x)−x+x2+1=ln(x2+1)−x2−x+x2+1=ln(−x+x2+1)
= f ( − x ) = ln ( − x + x 2 + 1 ) =f(-x)=\ln(-x+\sqrt{x^2+1}) =f(−x)=ln(−x+x2+1)
∴ \therefore ∴ y = a r s h x y=\mathrm{arsh}\ x y=arsh x 是奇函数。
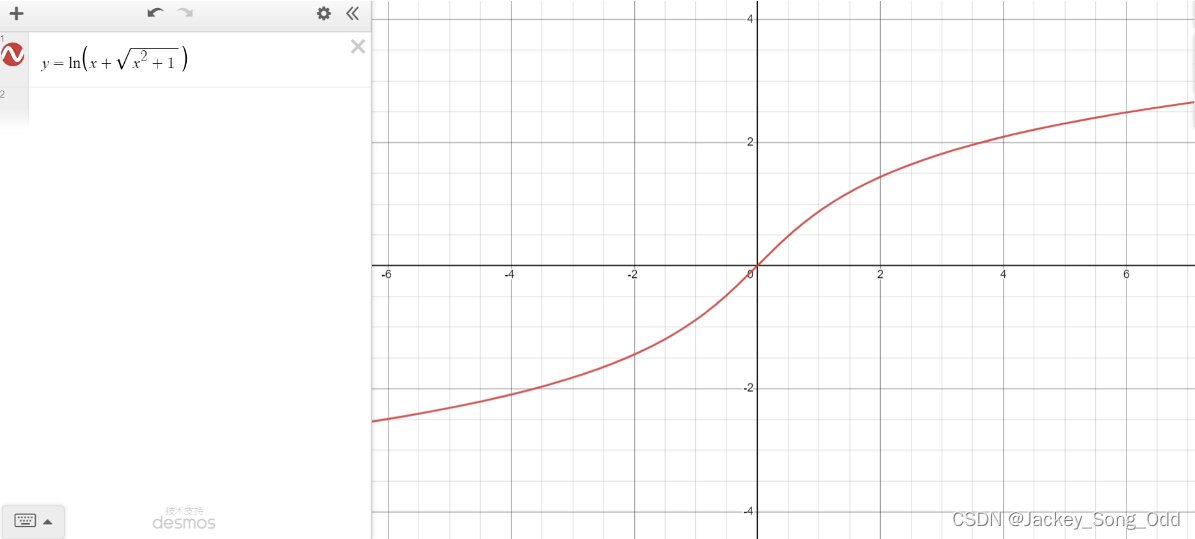
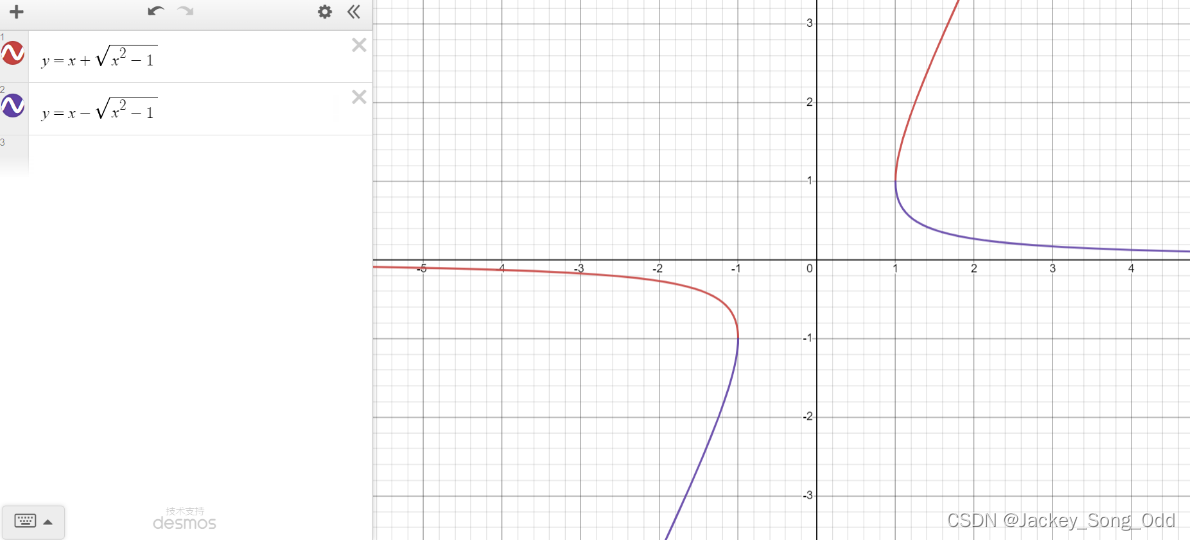
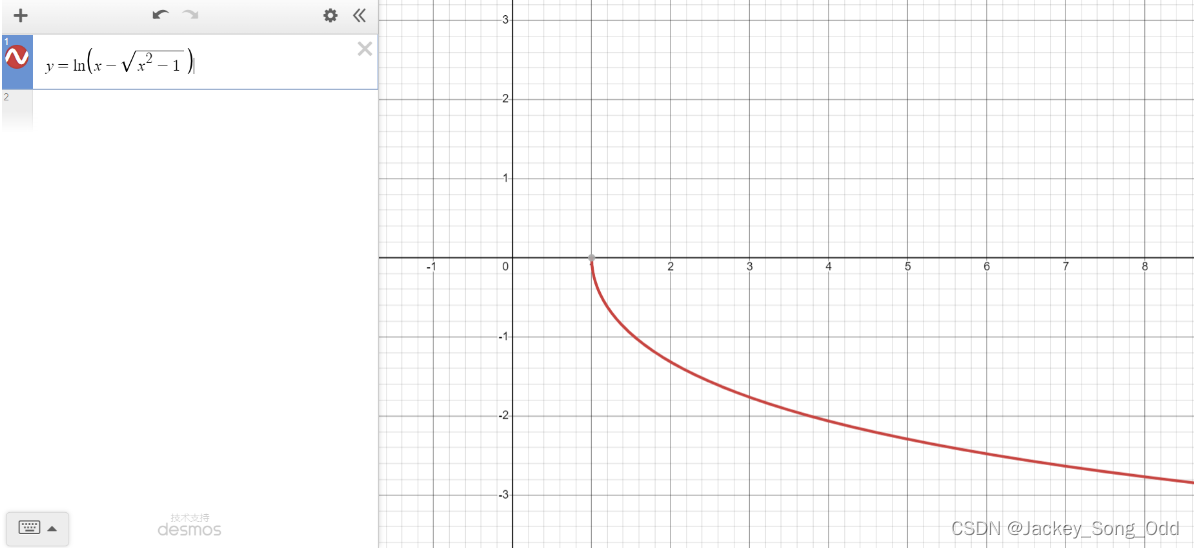
y = c h x y=\mathrm{ch}\ x y=ch x 的反函数 y = a r c h x = ln ( x + x 2 − 1 ) , x ≥ 1 y=\mathrm{arch}\ x=\ln(x+\sqrt{x^2-1}),\quad x\geq1 y=arch x=ln(x+x2−1),x≥1.
定义域:当 x < 0 x<0 x<0 时, x + x 2 − 1 x+\sqrt{x^2-1} x+x2−1 始终小于零,所以 x x x 不能小于零;
当 x > 0 x>0 x>0 时,只要满足 x 2 − 1 \sqrt{x^2-1} x2−1 根号下大于零即可,即 x ≥ 1 x\geq1 x≥1.
所以定义域为 [ 1 , + ∞ ) [1,+\infty) [1,+∞). 推导过程如下:
x = c h y , y ≥ 0 x=\mathrm{ch}\ y,\quad y\geq0 x=ch y,y≥0.
x = e y + e − y 2 , y ≥ 0 x=\dfrac{e^y+e^{-y}}{2},\quad y\geq0 x=2ey+e−y,y≥0.
令 u = e y u=e^y u=ey
x = u + 1 u 2 x=\dfrac{u+\dfrac{1}{u}}{2} x=2u+u1
u 2 − 2 x u + 1 = 0 u^2-2xu+1=0 u2−2xu+1=0
u = 2 x ± 4 x 2 − 4 2 = x ± x 2 − 1 > 0 u=\dfrac{2x\pm\sqrt{4x^2-4}}{2}=x\pm\sqrt{x^2-1}>0 u=22x±4x2−4=x±x2−1>0
x > 0 x>0 x>0 且 x 2 − 1 ≥ 0 x^2-1\geq0 x2−1≥0, ∴ x ≥ 1 \therefore x\geq1 ∴x≥1.
∵ u = e y > 0 , y ≥ 0 , u ≥ 1 \because u=e^y>0,\quad y\geq0,\quad u\geq1 ∵u=ey>0,y≥0,u≥1
∴ \therefore ∴ 取正号 u = x + x 2 − 1 u=x+\sqrt{x^2-1} u=x+x2−1.
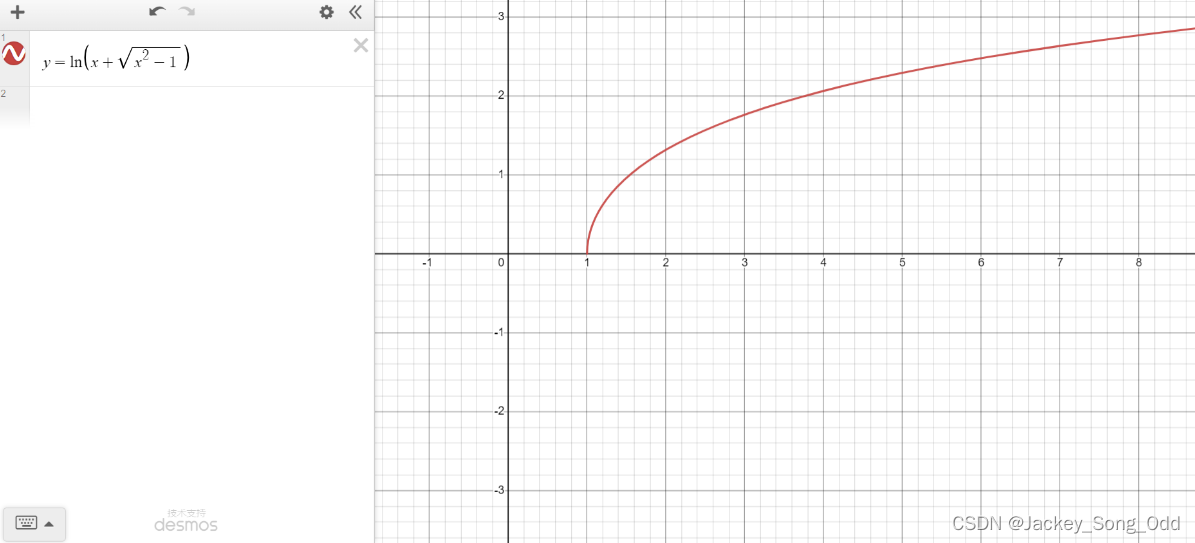
∴ y = a r c h x = ln ( x + x 2 − 1 ) , x ≥ 1 \therefore y=\mathrm{arch}\ x=\ln(x+\sqrt{x^2-1}),\quad x\geq1 ∴y=arch x=ln(x+x2−1),x≥1.
y = c h x , ( x ≥ 0 ) y=\mathrm{ch}\ x,\quad (x\geq0) y=ch x,(x≥0) 的反函数 y = a r c h x y=\mathrm{arch}\ x y=arch x 即反双曲余弦函数的图像:
y
=
c
h
x
,
(
x
≤
0
)
y=\mathrm{ch}\ x,\quad (x\leq0)
y=ch x,(x≤0) 的反函数
y
=
a
r
c
h
x
y=\mathrm{arch}\ x
y=arch x 即反双曲余弦函数的图像:
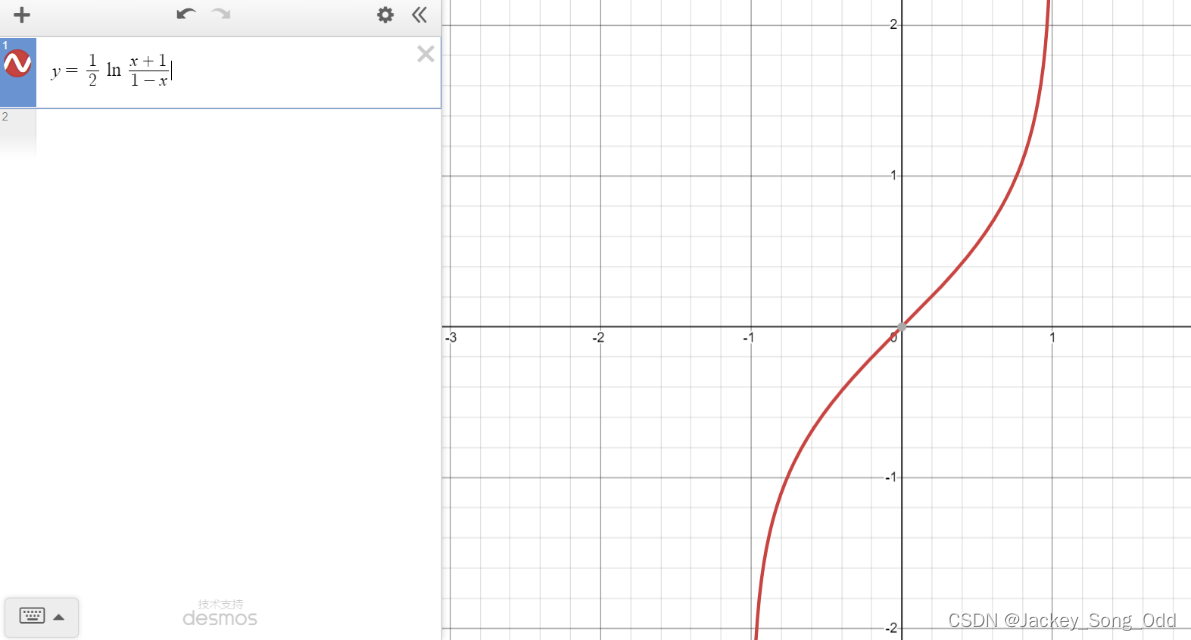
y = t h x = e x − e − x e x + e − x y=\mathrm{th}\ x=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} y=th x=ex+e−xex−e−x 的反函数 y = a r t h x = 1 2 ln 1 + x 1 − x , x ∈ ( − 1 , 1 ) y=\mathrm{arth}\ x=\dfrac{1}{2}\ln\dfrac{1+x}{1-x},\quad x\in (-1,1) y=arth x=21ln1−x1+x,x∈(−1,1). 下面是推导过程:
x = e y − e − y e y + e − y x=\dfrac{e^y-e^{-y}}{e^y+e^{-y}} x=ey+e−yey−e−y
令 u = e y u=e^y u=ey
x = u − 1 u u + 1 u x=\dfrac{u-\dfrac{1}{u}}{u+\dfrac{1}{u}} x=u+u1u−u1, ∵ u = e y > 0 \because u=e^y>0 ∵u=ey>0,分子分母同时乘以 u u u :
u = u 2 − 1 u 2 + 1 u=\dfrac{u^2-1}{u^2+1} u=u2+1u2−1
u 2 − 1 = u 2 x + x u^2-1=u^2x+x u2−1=u2x+x
( x − 1 ) u 2 = − x − 1 (x-1)u^2=-x-1 (x−1)u2=−x−1
u 2 = x + 1 1 − x u^2=\dfrac{x+1}{1-x} u2=1−xx+1
u = 1 + x 1 − x u=\sqrt{\dfrac{1+x}{1-x}} u=1−x1+x
u = e y = 1 + x 1 − x u=e^y=\sqrt{\dfrac{1+x}{1-x}} u=ey=1−x1+x
y = ln ( 1 + x 1 − x ) 1 2 = 1 2 ln 1 + x 1 − x y=\ln\Big(\dfrac{1+x}{1-x}\Big)^{\frac{1}{2}}=\dfrac{1}{2}\ln\dfrac{1+x}{1-x} y=ln(1−x1+x)21=21ln1−x1+x
1 + x 1 − x > 0 \dfrac{1+x}{1-x}>0 1−x1+x>0
x ≠ 1 x\neq1 x=1
当 x < 1 x<1 x<1 时, 1 + x > 0 1+x>0 1+x>0 得: x > − 1 x>-1 x>−1
当 x > 1 x>1 x>1 时, 1 + x < 0 1+x<0 1+x<0 得: x < − 1 x<-1 x<−1,不成立。
所以定义域为 ( − 1 , 1 ) (-1,1) (−1,1).
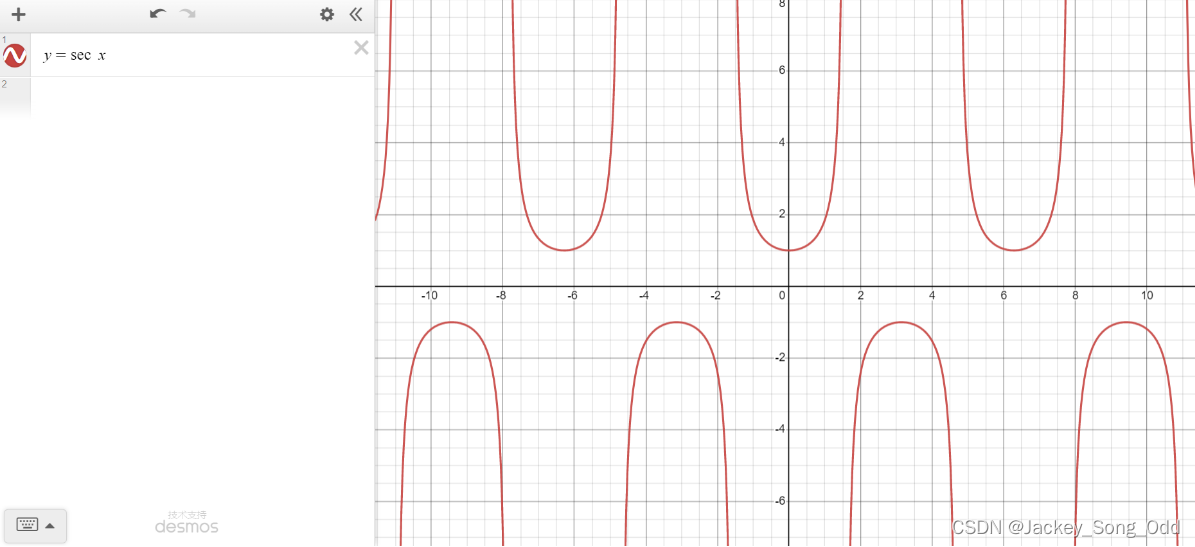
y = sec x = 1 cos x y=\sec x=\dfrac{1}{\cos x} y=secx=cosx1, cos x ≠ 0 \cos x\neq0 cosx=0, x ≠ 2 k π ± π 2 , k ∈ Z x\neq 2k\pi\pm\dfrac{\pi}{2},k\in\mathrm{Z} x=2kπ±2π,k∈Z.
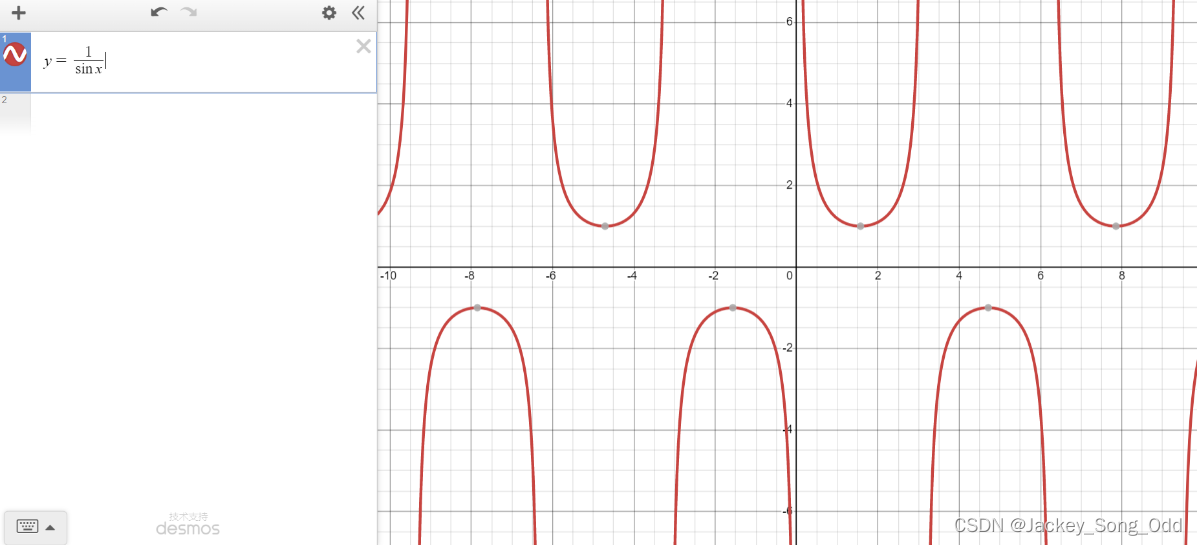
y = csc x = 1 sin x y=\csc x=\dfrac{1}{\sin x} y=cscx=sinx1, sin x ≠ 0 \sin x\neq 0 sinx=0, x ≠ k π , k ∈ Z x\neq k\pi,k\in\mathrm{Z} x=kπ,k∈Z.
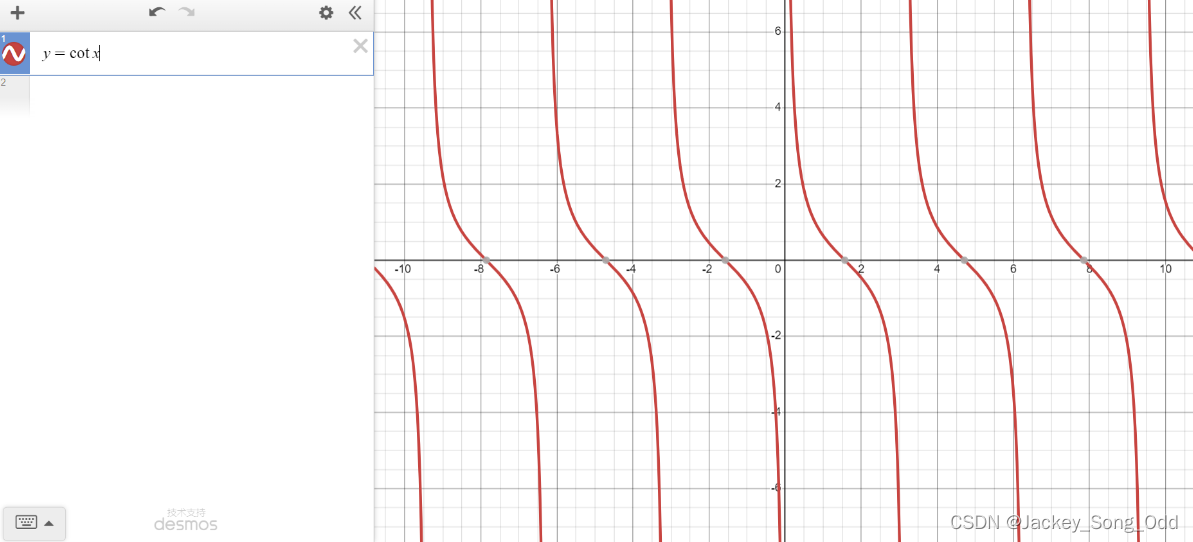
y = cot x = cos x sin x = 1 tan x y=\cot x=\dfrac{\cos x}{\sin x}=\dfrac{1}{\tan x} y=cotx=sinxcosx=tanx1, tan x ≠ 0 \tan x\neq 0 tanx=0, x ≠ k π , k ∈ Z x\neq k\pi,k\in\mathrm{Z} x=kπ,k∈Z.