题目描述
题目链接:[LeetCode 1775]通过最少操作数使数组的和相等
给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间(包含 1 和 6)。
每次操作中,你可以选择 任意 数组中的任意一个整数,将它变成 1 到 6 之间 任意 的值(包含 1 和 6)。
请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等,请返回 -1 。
示例1
输入:nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
输出:3
解释:你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums2[0] 变为 6 。 nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[5] 变为 1 。 nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[2] 变为 2 。 nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2] 。
示例2
输入:nums1 = [1,1,1,1,1,1,1], nums2 = [6]
输出:-1
解释:没有办法减少 nums1 的和或者增加 nums2 的和使二者相等。
示例3
输入:nums1 = [6,6], nums2 = [1]
输出:3
解释:你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums1[0] 变为 2 。 nums1 = [2,6], nums2 = [1] 。
- 将 nums1[1] 变为 2 。 nums1 = [2,2], nums2 = [1] 。
- 将 nums2[0] 变为 4 。 nums1 = [2,2], nums2 = [4] 。
思路分析
思考:如何使得操作数最小?
贪心!每次挑选靠近边缘的值,要将整个数组变大,挑选1让其变成6可以让整个数组变大5,而挑选3最多变成6,只能让数组变大6-3=3
如图:要让数组2尽可能变大,所以第一次选择1变成6,差距缩减到25-15=10
第二次选择第二个1变成6,差距缩减到25-20=5
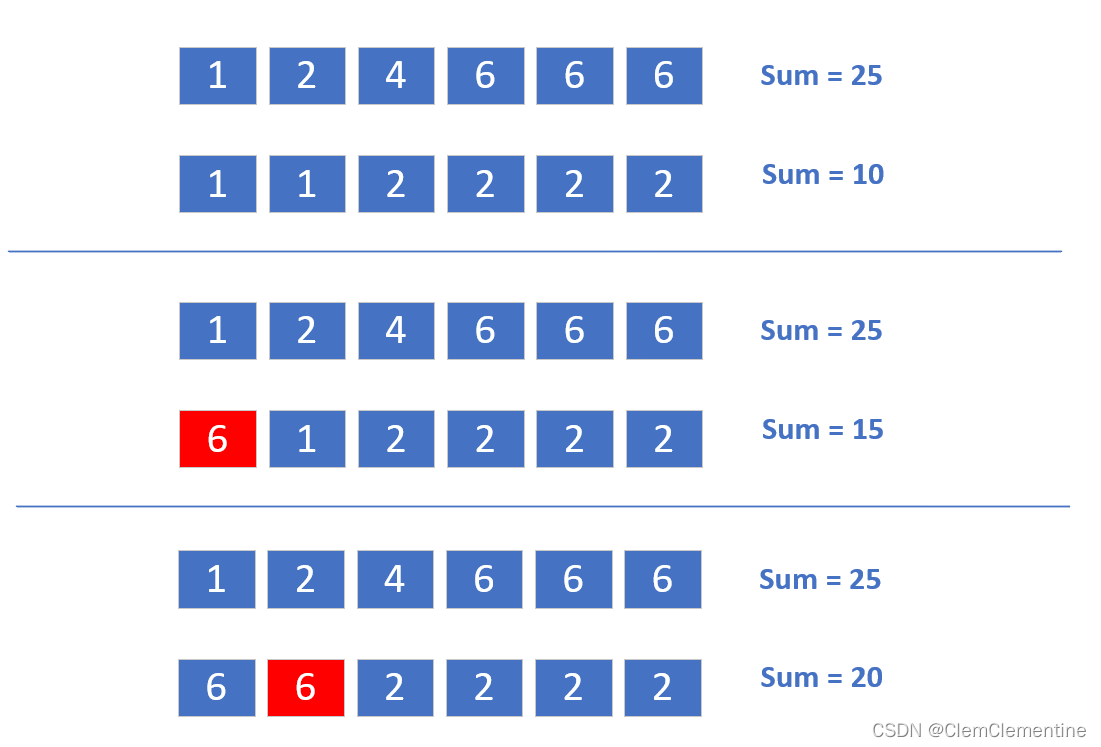
此时,第二个数组没有1了,最小是2,所以2的变化最多为4(因为6-2=4),还需要至少两步才能变到与数组1和相等,此时应该选择第一个数组中的6变成1,只需要一步就行
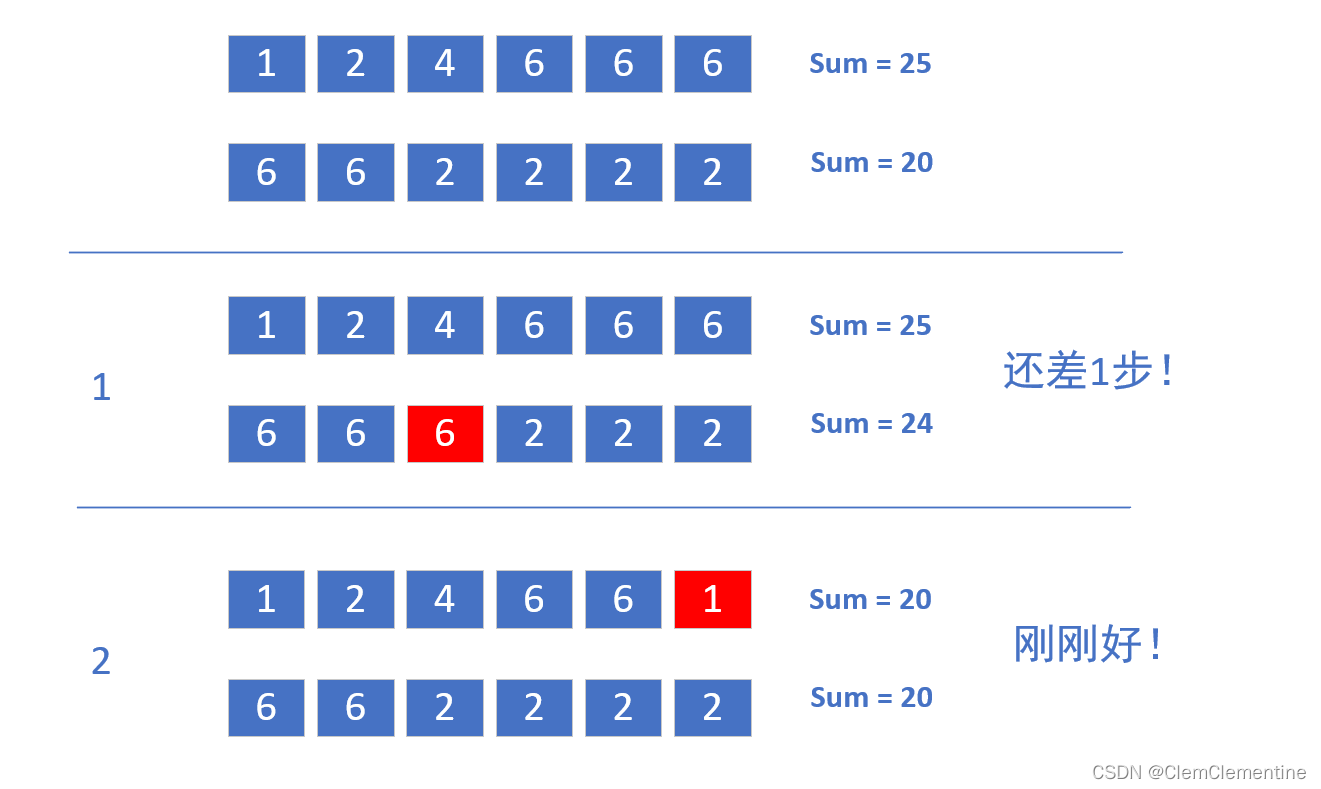
所以很明确了,我们要利用指针,指向小数组里面的最小值,和大数组里面的最大值,因为这样的数具有最大的变化能力!
代码(写得比较长,仅供参考)
class Solution {
public:
int check(int q1[], int q2[], int s1, int s2) {
//默认s1 < s2,方便计算
if(s1 > s2) return check(q2, q1, s2, s1);
//p1指向小数组最小值,p2指向大数组最大值,cnt记录当前两个数组差值
int p1 = 1, p2 = 6, res = 0, cnt = s2 - s1;
while(cnt) {
//如果走到头了,即小数组所有数都变为6,大数组所有数都变成1,还不够,说明不可能
if(p1 >= 6 || p2 <= 1) break;
//如果cnt > 0, 且p1这个位置有数
if(cnt && q1[p1]) {
//如果所有的p1都变成6,还是不足以将cnt填平
if(cnt > q1[p1] * (6 - p1)) {
cnt -= q1[p1] * (6 - p1);
res += q1[p1];
q1[6] += q1[p1];
} else {
//如果可以把cnt填平,那么只需要cnt / (6 - p1)上取整这么多次就可以
int t = (cnt + 5 - p1) / (6 - p1);
cnt = 0;
res += t;
q1[p1] -= t;
}
}
p1++;
//同理
if(cnt && q2[p2]) {
if(cnt > q2[p2] * (p2 - 1)) {
cnt -= q2[p2] * (p2 - 1);
res += q2[p2];
q2[p2] = 0;
} else {
int t = (cnt + p2 - 2) / (p2 - 1);
cnt = 0;
res += t;
q2[p2] -= t;
}
}
p2--;
}
if(cnt) return -1;
else return res;
}
int minOperations(vector<int>& nums1, vector<int>& nums2) {
int s1 = 0, s2 = 0, q1[7], q2[7];
int n = nums1.size(), m = nums2.size();
memset(q1, 0, sizeof q1);
memset(q2, 0, sizeof q2);
for (int i = 0; i < n; i++) {
s1 += nums1[i];
q1[nums1[i]]++;
}
for (int i = 0; i < m; i++) {
s2 += nums2[i];
q2[nums2[i]]++;
}
if(s1 == s2) return 0;
else {
return check(q1, q2, s1, s2);
}
}
};