【复习《剑指Offer》6-12题】【每天40分钟，我们一起用50天刷完 (剑指Offer)】第七天 7/50

news2024/9/30 21:19:58

专注效率记忆
预习笔记复习做题

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

本博客带大家一起学习，我们不图快，只求稳扎稳打。
由于我高三是在家自学的，经验教训告诉我，学习一定要长期积累，并且复习，所以我推出此系列。
只求每天坚持40分钟，一周学5天，复习2天
也就是一周学10道题
50天后我们就可以学完76道题，相信50天后，我们一定可以有扎实的代码基础！我们每天就40分钟，和我一起坚持下去吧！
qq群：866984458

本题出自 acwing网站
这个系列是免费的
打卡即刻退回费用。

第七天【剑指Offer例题代码系列】

- 6. 重建二叉树
- - - 根据前序遍历和中序遍历得到树
  - 补充题：树的遍历
- 7. 二叉树的下一个节点
- 8. 用两个栈实现队列
- - - 补充：copy(a,b) 把a赋值给b
- 9. 斐波那契数列
- 10. 旋转数组的最小数字
- 11. 矩阵中的路径
- 12. 机器人的运动范围

6. 重建二叉树

原题链接

在这里插入图片描述

根据前序遍历和中序遍历得到树

过程如下：

首先根据前序遍历找到根节点
找到中序遍历中，该根节点的位置
中序中位于根节点左边的就是左子树，右边的就是右子树
由于我们需要在中序遍历中找到根节点的位置，那么每次都需要遍历中序遍历，不如直接用unordered_map存储数值和位置
便于写代码，我们可以每次把mp[根节点] 的位置用变量表示出来

在这里插入图片描述

本题的代码不需要死记硬背

就需要明白

由前序确定根节点
由中序确定左右子树的个数
由左右子树的个数确定下一个根节点的位置

根据这三点去写代码即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    unordered_map<int,int> pos;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for (int i = 0; i < n; i ++ )
            pos[inorder[i]] = i;
        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
    {
        if (pl > pr) return NULL;
        int k = pos[pre[pl]] - il;
        TreeNode* root = new TreeNode(pre[pl]);
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }
};

补充题：树的遍历

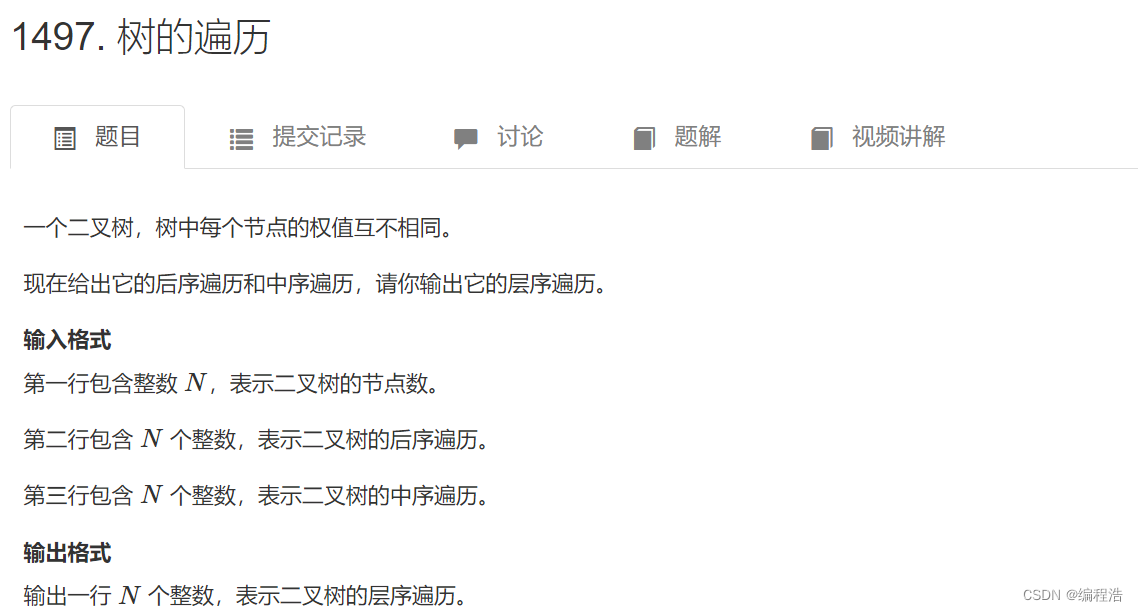
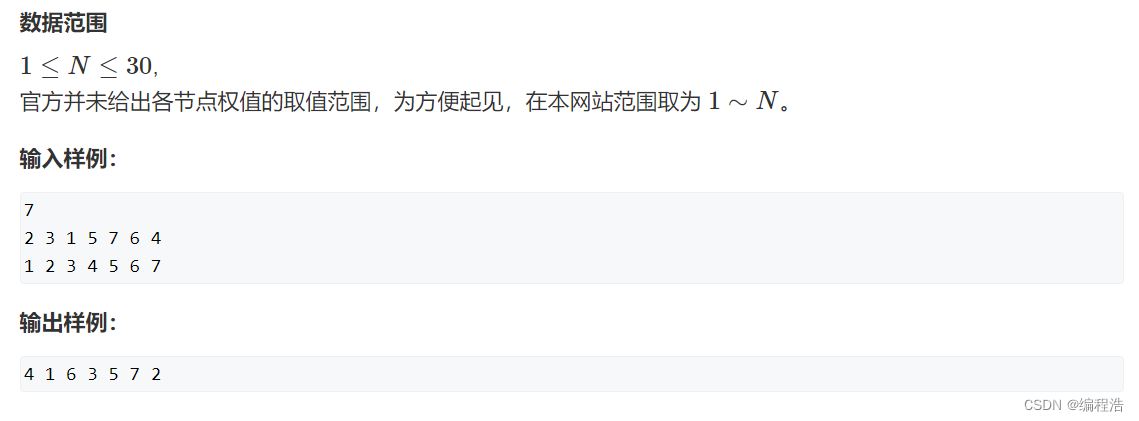
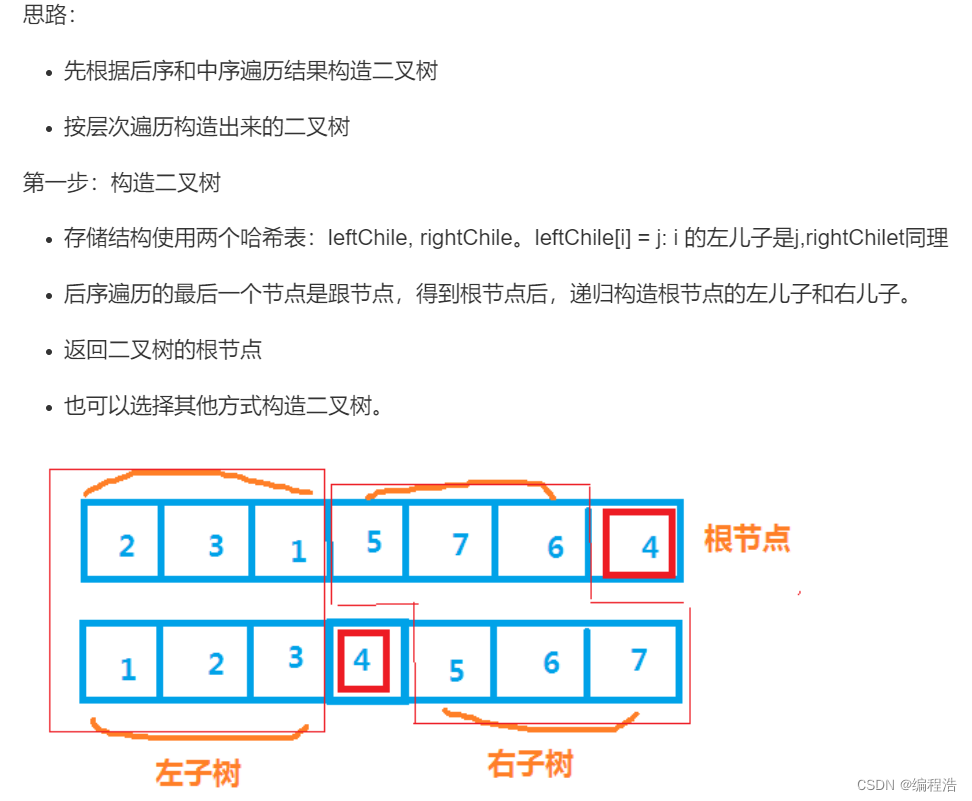
在这里插入图片描述

#include <iostream>
#include <string>
#include <unordered_map>
#include <vector>
#include <algorithm>
#include<memory>
using namespace std;

const  int N = 35;
int n;
int inorder[N], postorder[N];
unordered_map<int, int > leftChile, rightChile;//哈希表保存树，leftChile[i] = j: i 的左儿子是j,rightChilet同理
unordered_map<int, int > h;//保存中序遍历中各节点的位置

int dfs(int postorder[], int inorder[], int l1, int r1, int l2, int r2)//构造二叉树
{   
    if (l1 > r1) return 0;//没有节点，返回0
    int root = postorder[r1];//根结点为后续遍历的最后一个节点

    int k = h[root];//找到根节点在序遍历中的位置

    leftChile[root] = dfs(postorder, inorder, l1, k - 1 - l2 + l1, l2, k - 1);//构造左儿子
    rightChile[root] = dfs(postorder, inorder,r1-1 - (r2 - (k +1)) , r1 -1, k + 1, r2);//构造右儿子

    return root;
}

int main()
{
    cin >> n;//输入
    for (int i = 0; i < n; i++)
        cin >> postorder[i];

    for (int i = 0; i < n; i++)
    {
        cin >> inorder[i];
        h[inorder[i]] = i;//保存中序遍历中各个节点的位置
    }
    int root = dfs(postorder, inorder, 0, n - 1, 0, n - 1);//构造二叉树

    //数组模拟队列
    int q[N], hh = 0, tt = -1;//按层次遍历
    if (root)//非0 表示有节点
        q[++tt] = root;

    while (hh <= tt)
    {
        int t = q[hh++];
        if (leftChile[t]) q[++tt] = leftChile[t];//非0 为节点，入队列
        if (rightChile[t]) q[++tt] = rightChile[t];//非0 为节点，入队列
    }
    for (int i = 0; i <= tt; i++)//队列中保存的就是按层次遍历的结果
        cout << q[i] << " ";
    return 0;
}

7. 二叉树的下一个节点

原题链接

中序遍历：左根右

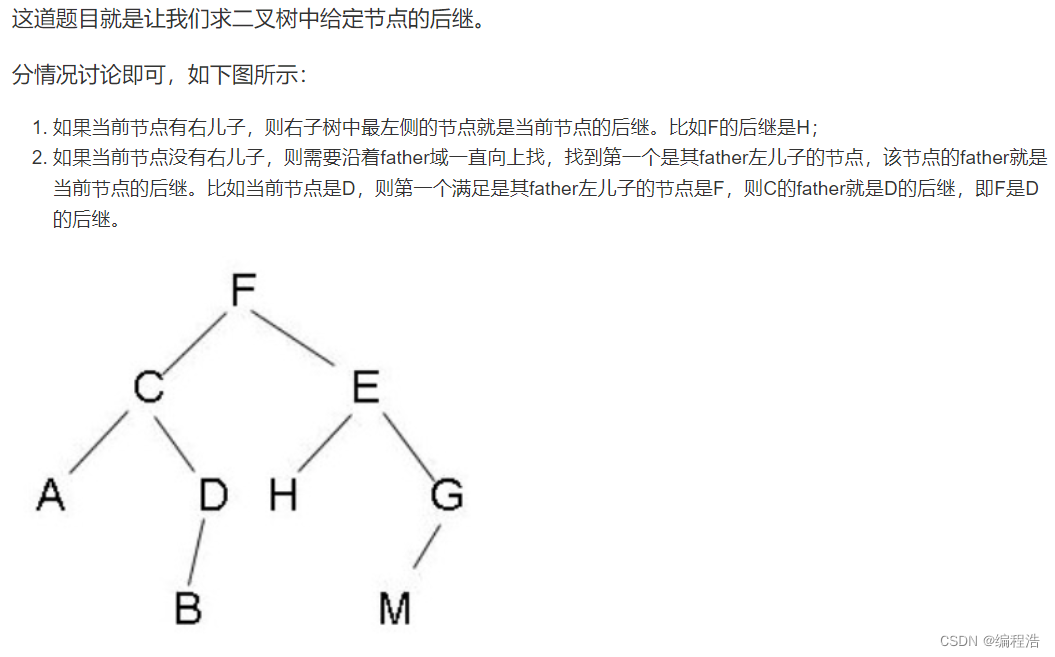
在这里插入图片描述

本题要分析节点的特点

如果节点有右子树，那么右子树的最左边的节点就是该节点后序
如果没有右子树，会有三种可能，在代码中有体现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode father;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    /**
     * 模拟
     * 时间复杂度：O(height)，height 为二叉树的高度
     * 空间复杂度：O(1)
     */
    public TreeNode inorderSuccessor(TreeNode p) {
        TreeNode node = p;
        // Case 1. 如果该节点有右子树，那么下一个节点就是其右子树中最左边的节点
        if (node.right != null) {
            node = node.right;
            while (node.left != null) {
                node = node.left;
            }
            return node;
        }
            
        if(node.father != null && node.father.left == node)
            return node.father;
        if(node.father != null && node.father == null)
            return null;
        while(node.father!=null && node.father.right == node)
        {
            node = node.father;
        }
        return node.father;
    }
}

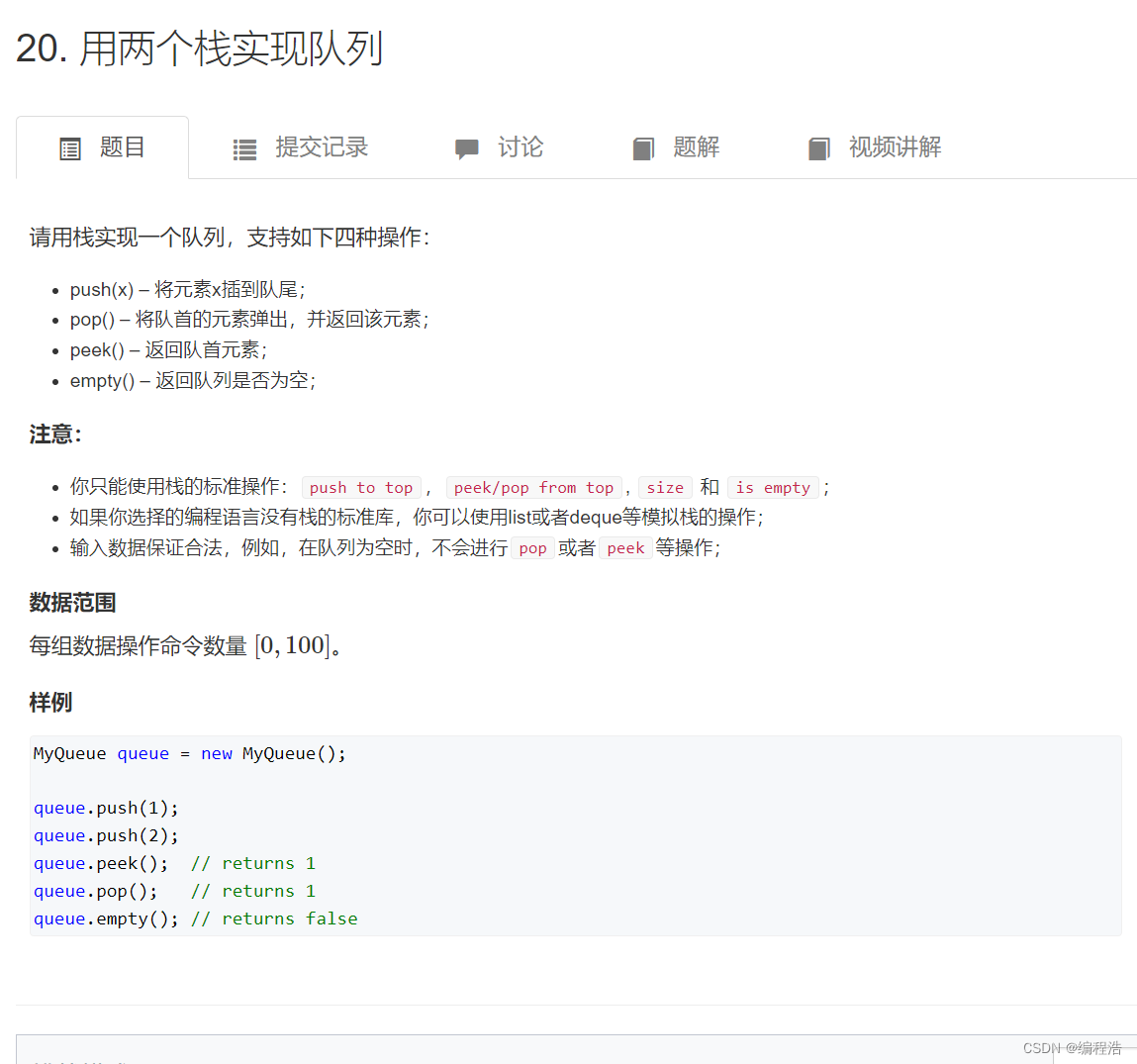
8. 用两个栈实现队列

原题链接

补充：copy(a,b) 把a赋值给b

在这里插入图片描述

class MyQueue {
public:
    /** Initialize your data structure here. */
    stack<int> stk, cache;
    MyQueue() {

    }

    /** Push element x to the back of queue. */
    void push(int x) {
        stk.push(x);
    }

    void copy(stack<int> &a, stack<int> &b) {
        while (a.size()) {
            b.push(a.top());
            a.pop();
        }
    }

    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        copy(stk, cache);
        int res = cache.top();
        cache.pop();
        copy(cache, stk);
        return res;
    }

    /** Get the front element. */
    int peek() {
        copy(stk, cache);
        int res = cache.top();
        copy(cache, stk);
        return res;
    }

    /** Returns whether the queue is empty. */
    bool empty() {
        return stk.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * bool param_4 = obj.empty();
 */

9. 斐波那契数列

原题链接

class Solution {
    public int Fibonacci(int n) {
        if(n==1||n==2)
            return 1;
         int a = 0,b = 0,c = 0;
         a = 1;
         b = 1;
         for(int i = 3; i <= n; i++)
         {
             c = a + b;
             a = b;
             b = c;
         }
         return c;
    }
}

10. 旋转数组的最小数字

在这里插入图片描述

原题链接

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size() == 0)
            return -1;
        if(nums.size() == 1)
            return nums[0];
        
        for(int i = 0; i < nums.size()-1; i++)
        {
            if(nums[i] > nums[i+1])
            {
                return nums[i+1];
            }
        }
        return nums[0];
    }
};

11. 矩阵中的路径

原题链接
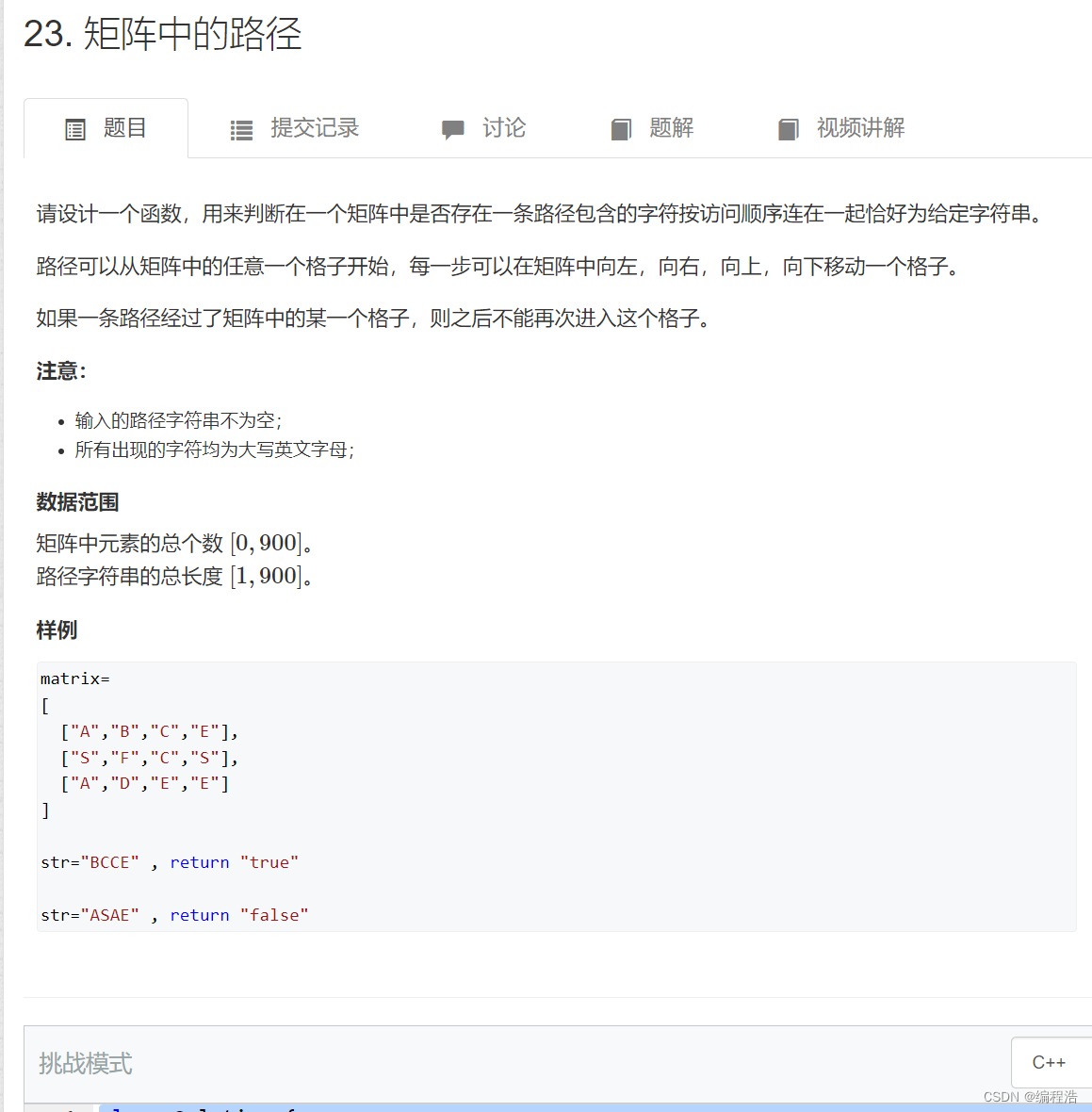
在这里插入图片描述
这道题就是一个经典的dfs问题（不懂dfs的可以csdn中搜索dfs算法经典例题）

本道题需要注意的是
行和纵坐标
行个数
matrix.size()
纵坐标个数
matrix[i].size()


class Solution {
public:
    bool st[1000][1000];
    
    bool hasPath(vector<vector<char>>& matrix, string &str) {
        memset(st,false,sizeof st);
        for(int i = 0; i < matrix.size(); i++)
        {
            for(int j = 0; j < matrix[i].size(); j++)
            {
                if(matrix[i][j] == str[0])
                {
                    st[i][j] = true;
                    if(dfs(matrix,str,i,j,1)==true)
                        return true;
                    st[i][j] = false;
                }
            }
        }
        return false;
    }
    
    bool dfs(vector<vector<char>>& matrix, string &str,int x,int y,int u)
    {
        if(str.size()==u)
            return true;
        int dx[4] = {1,-1,0,0};
        int dy[4] = {0,0,1,-1};
        
        for(int i = 0; i < 4; i++)
        {
            int a = x + dx[i];
            int b = y + dy[i];
            if(a >= 0 && a < matrix.size() && b >= 0 && b < matrix[a].size() && st[a][b] == false && matrix[a][b] == str[u])
            {
                st[a][b] = true;
                if(dfs(matrix,str,a,b,u+1)==true)
                    return true;
                st[a][b] = false; 
            }
        }
        return false;
    }
    
};

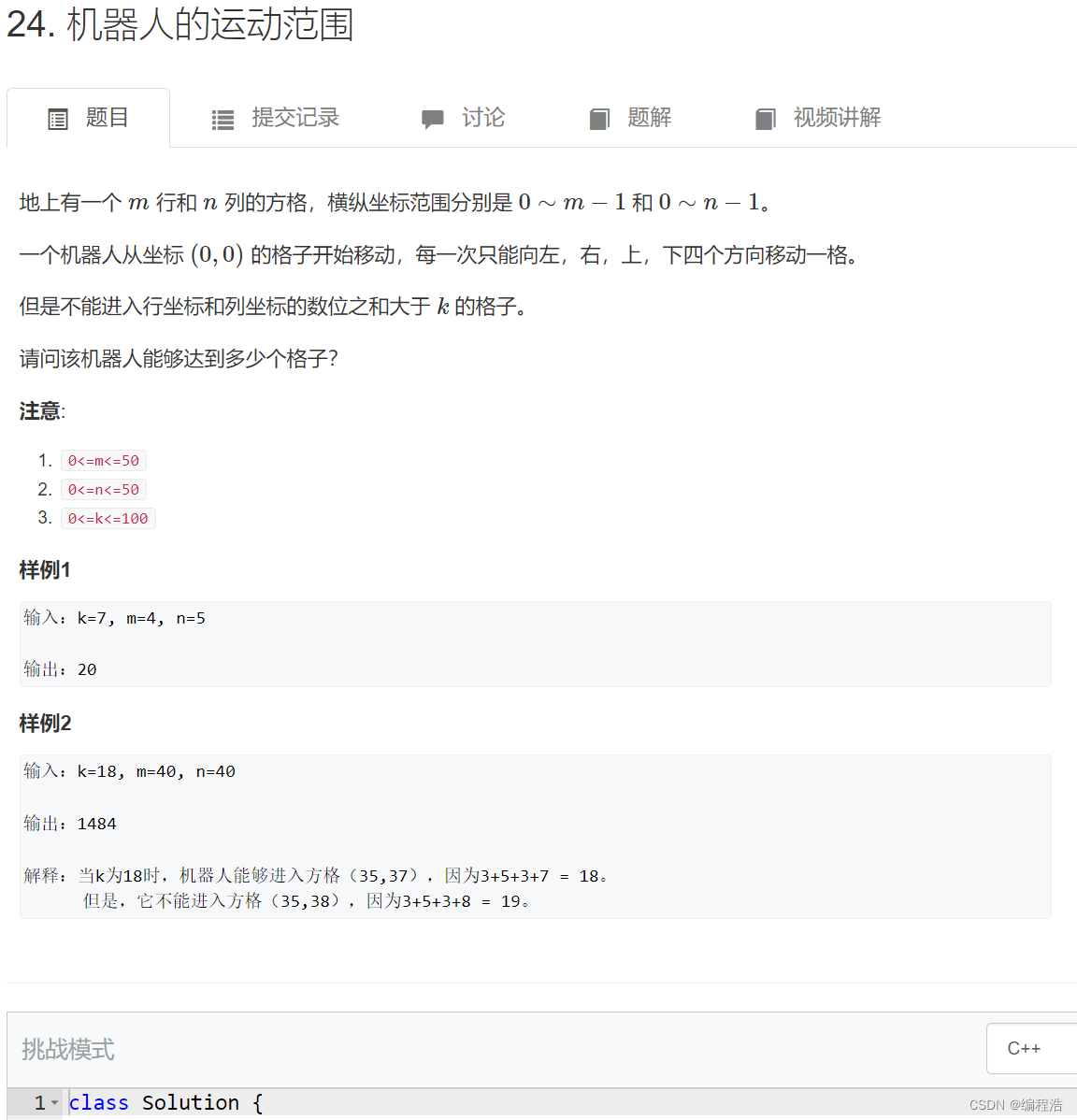
12. 机器人的运动范围

原题链接

这是一道经典的bfs问题
在这里插入图片描述

class Solution {
public:

    int check(int a,int b)
    {
        int sum = 0;
        while(a)
        {
            sum += a%10;
            a = a/10;
        }
        while(b)
        {
            sum += b%10;
            b = b/10;
        }
        return sum;
    }

    int movingCount(int threshold, int rows, int cols)
    {
        if(rows==0 || cols == 0)
            return 0;
        int cnt = 0;
        bool st[110][110];
        queue<pair<int,int>> q;
        q.push({0,0});
        st[0][0] = true;
        
        while(q.size())
        {
            auto t = q.front(); q.pop();
            cnt++;
            int dx[4] = {1,-1,0,0};
            int dy[4] = {0,0,1,-1};
            
            for(int i = 0; i < 4; i++)
            {
                int a = dx[i] + t.first;
                int b = dy[i] + t.second;
                
                if(a>=0 && a<rows && b>=0 && b<cols && check(a,b) <= threshold && st[a][b] == false)
                {
                    st[a][b] = true;
                    q.push({a,b});
                }
            }
        }
        return cnt;
    }
};