《深度学习入门:基于python的理论与实现》chap2感知机

news2024/10/1 5:27:15

文章目录

2.1 什么是感知机
2.2 简单逻辑电路 &2.3 感知机的实现
- 引入偏置
- 与门 And gate
- 与非门(NAND gate)
- 或门 OR gate
2.4 感知机的局限性(单层感知机无法分离非线性空间)
- 2.4.1 异或门
- 2.4.2 线性和非线性
2.5 多层感知机(multi-layered perception)
- 2.5.1 已有门电路的组合
- 2.5.2 异或门的实现
2.6 从与非门到计算机
2.7 小结

入坑AI的时候就是看的这本书，当时比较粗略地看到了第六章，没有记笔记，现在来重温一下，力求建立自己的知识体系

本chap学习感知机(perceptron)这一算法并利用感知机解决一些简单的问题。感知机是由美国学者Frank Rosenblatt在1957年提出来的。

严格地讲，本章中所说的感知机应该称为“人工神经元”或“朴素感知机”，但是因为很多基本的处理都是共通的，所以这里就简单地称为“感知机”。

2.1 什么是感知机

既然是再次看这本书，就尝试自己总结和概况

我觉得学习计算机要实时秉持输入经过某个function得到输出的观念，感知机，从字面上看，感知一些东西，经过某个function，做出反应，那么感知的东西就是输入，作出的反应就是输出

那么输入是什么呢？
- 感知机会接收信号，这里的信号取值是0或1
  - 0对应不传递信号
  - 1对应传递信号
function是什么？
- 使得每个输入信号乘以其固定的权重(weight)再相加
输出是什么？
- 这些信号分别与他们的权重相乘之后再相加的结果，也作为一个信号输出，也是0或1
- 那么什么情况会输出1(称为“神经元被激活”)，什么时候输出0呢
  - 前面说的相加的结果，也就是信号的总和，会和一个界限值进行比较，这个界限值称为阈值(threshold)

图示和数学表达式
- 图示
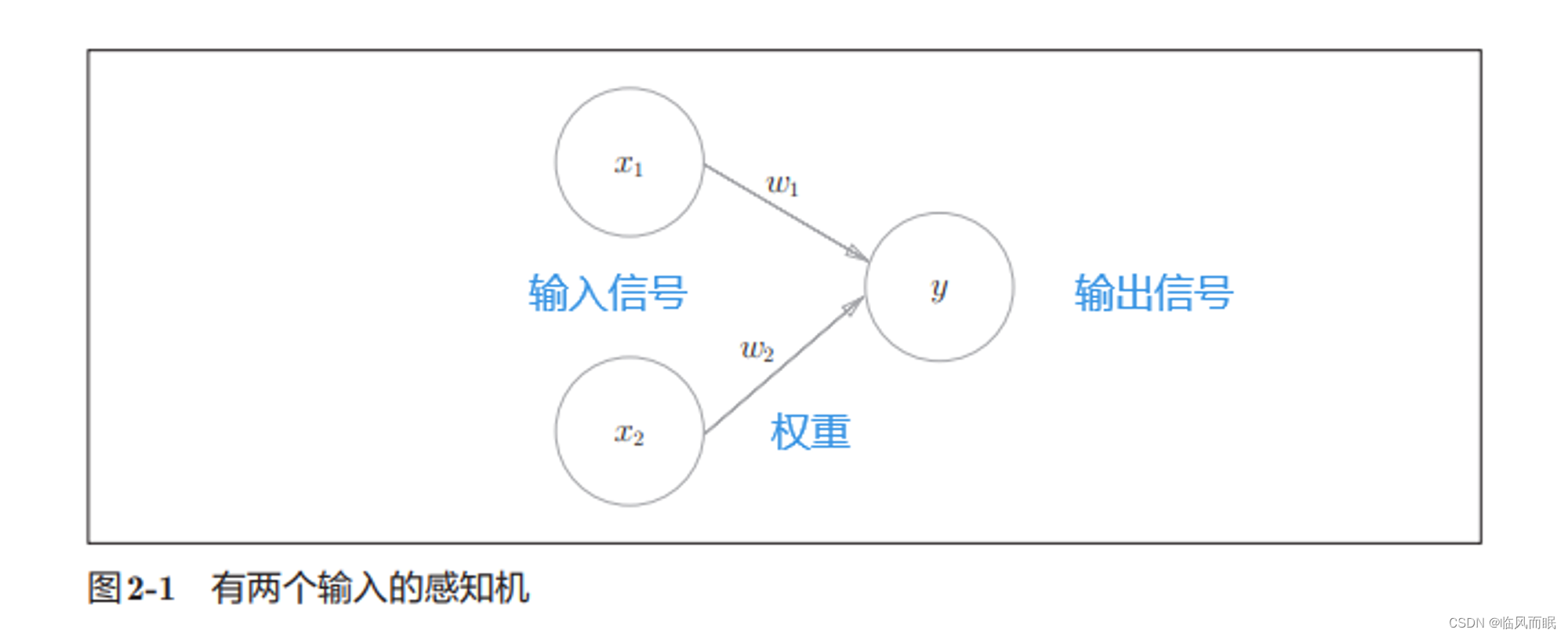
- 数学表达式

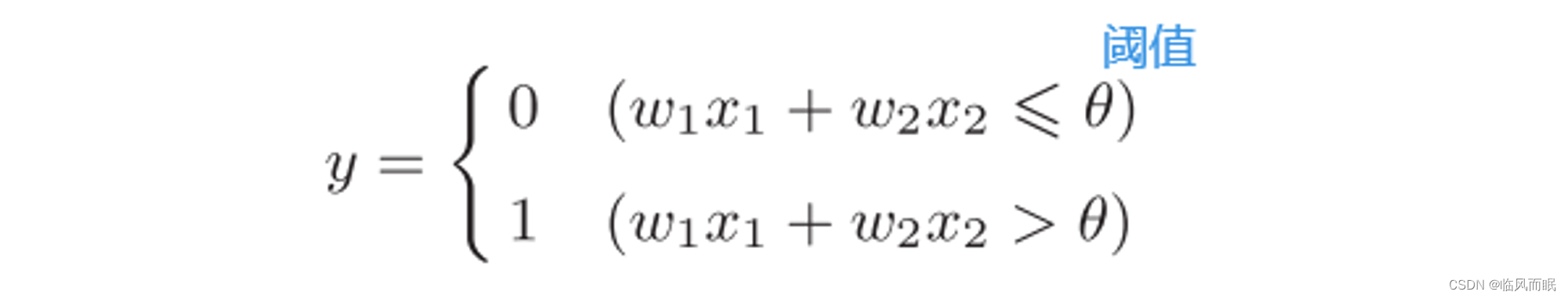
2.2 简单逻辑电路 &2.3 感知机的实现

引入偏置

把前面的式子变一变，这里把−θ命名为偏置b,偏置的值决定了神经元被激活的容易程度。

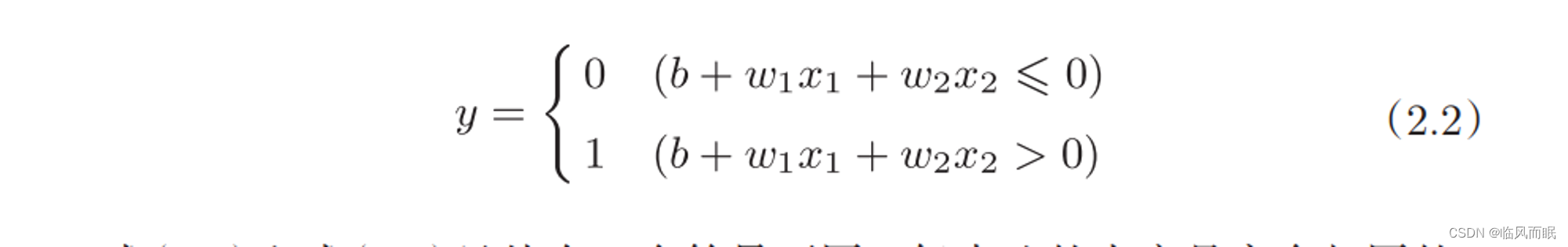
在这里插入图片描述

w1和w2是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为1的程度）的参数。

比如，若b为 −0.1，则只要输入信号的加权总和超过0.1，神经元就会被激活。但是如果b 为−20.0，则输入信号的加权总和必须超过20.0，神经元才会被激活。

哈哈在数电里面学过了这些gates，那这里就记录一些英文表达

与门 And gate

我们尝试找一个能实现与门功能的感知机，与门的输入输出我们知道了，那就是要找剩下的几个参数，两个权重和一个阈值

书上给的这个例子 0.5，0.5，0.7

tmp那里是把前面的数学公式右边减到左边来了，当且仅当x1=1,x2=1时，0.5x1+0.5x1>0.7

# coding: utf-8
import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = AND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

(0, 0)->0
(1, 0)->0
(0, 1)->0
(1, 1)->1

有无数组参数都可以做到，比如

    w = np.array([0.6, 0.5])
    b = -0.95

回忆一下数电，输入的0表示低电平，1表示高电平，输出也是两种情况，低电平or高电平
- 中间也是经历了一些计算，不过那个涉及模电了，不是这种简单的感知机

与非门(NAND gate)

NAND ，即Not AND

与非门就是颠倒了与门的输出
要表示与非门，可以用(w1, w2, θ) = (−0.5, −0.5, −0.7) 这样的组合（其他的组合也是无限存在的）。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门

代码实现

# coding: utf-8
import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

或门 OR gate

我们来思考一下参数，根据或或门的特点，w1和w2都要比θ大，然后θ>=0即可

也就是 0<=θ< min[w1,w2]

θ=-b（代码里面）

code

# coding: utf-8
import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

2.4 感知机的局限性(单层感知机无法分离非线性空间)

2.4.1 异或门

异或门也被称为逻辑异或电路，x1和x2相同时，输出0，不同时输出1

哈哈哈我记得大一学C语言的时候，异或和同或总是傻傻分不清🤣😓😓😓

前面的感知机能否实现这个异或门呢
之前在凑前几个参数的具体值的时候，我是将00,y ；01,y；10,y；11,y四种情况代入进去分析的
再来看看书上是如何分析的
- 将或门的动作形象化。或门的情况下，当权重参数 (b, w1, w2) = (−0.5, 1.0, 1.0)时可满足真值表
  - 感知机会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1，另一个空间输出0
    - 或门在(x1, x2) = (0, 0)时输出0，在(x1, x2)为(0, 1)、(1, 0)、(1, 1)时输出1。图2-6中，○表示0，△表示1
    - 如果想制作或门，需要用直线将图2-6中的○和△分开。实际上，刚才的那条直线就将这4个点正确地分开了
- 换成异或门还能找条直线来分开吗？
  
  其实和我前面推导的式子来理解也一样，直线的斜率一会儿大于0，一会儿小于0，分不开的

2.4.2 线性和非线性

图2-7中的○和△无法用一条直线分开，但是如果将“直线”这个限制条件去掉，就可以实现了。比如，我们可以像图2-8那样，作出分开○和△的空间。
感知机的局限性就在于它只能表示由一条直线分割的空间。图2-8这样弯曲的曲线无法用感知机表示。另外，由图2-8这样的曲线分割而成的空间称为 非线性空间，由直线分割而成的空间称为线性空间。线性、非线性这两个术语在机器学习领域很常见，可以将其想象成图2-6和图2-8所示的直线和曲线。

2.5 多层感知机(multi-layered perception)

虽然无法利用一个感知机直接实现异或门，但是我们能不能叠加多层来实现呢？Yes
- 异或门的制作方法有很多，其中之一就是组合我们前面做好的与门、与非门、或门进行配置
实际上，与门、或门是单层感知机，而异或门是2层感知机。叠加了多层的感知机也称为多层感知机（multi-layered perceptron）

2.5.1 已有门电路的组合

书上给了这种做法

（与非）和（或）再与

2.5.2 异或门的实现

code

# coding: utf-8
from and_gate import AND
from or_gate import OR
from nand_gate import NAND

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))