简介

前面的文章介绍了如何在已知空间点的情况下在不同坐标系中的表示（刚体的坐标变换），以及如何将空间中的点投影到相机中生成图像，但是现实中的情况却是相反的情况（空间点以及坐标系之间的变换未知），这也正是SLAM要求解的问题。我们知道的只是一张张的图像以及像素在图像中的位置（2D），或者知道空间中的点在相机坐标系下的三维位置（3D）、或者知道一部分空间位置和其在图像像素中的位置，那么如何求解图像中所有或者部分像素点的位置就是SLAM要求解的问题，针对以上三种情况，有如下几种求解方式：

1 只知道图像中的像素点（2D-2D): 对极几何
2 知道图像中的点以及深度信息（3D-3D):ICP
3 知道图像的3D点以及对应的2D点（3D-2D）：PnP

变换或者投影时我们是将同一个点映射到不同的图像中，而通过像素点来反求解运动和地图点时，我们是通过不同的图像求解同一个空间点，因此需要找到同一个点在不同图像中的位置，这就是SLAM中的数据关联问题，该文章假设已经完成了数据的关联问题。

求解相机相对位姿

概念

极平面：

空间点P、两个位置相机光心O三个点构成的平面

极线

极平面与相机成像平面的交线l

极点

相机光心和成像平面的交点e
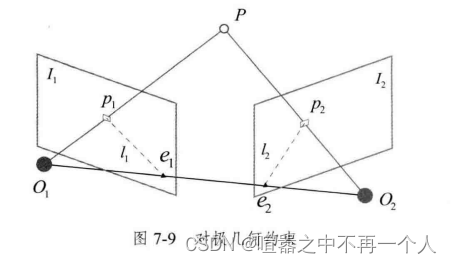
在这里插入图片描述

几何约束的作用

描述空间点、相机光心在同一平面、从而构建约束条件，求解相机运动

利用几何约束求解R/t

1 推导几何约束公式

1 建立投影模型和坐标变换模型：首先构建空间点P在两个图像中的投影关系，P为第一帧相机坐标系下的坐标
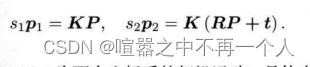
2 将P归一化，使其失去深度信息，p₁为像素点的其次坐标，归一化相当于将把P的空间位置，投影到归一化平面。
3 通过内参反求归一化坐标P（x₁、x₂代表P在两个相机的归一化平面坐标）
4 带入坐标转换模型得到约束方程
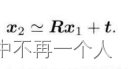
5 （处理方程）同时左乘t的反对称矩阵和x₂的转置
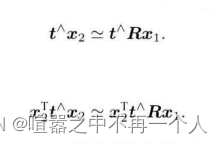
6 利用叉乘和点乘的概念得到约束方程并带入归一化投影方程得到对极几何约束

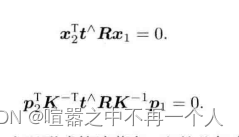
在这里插入图片描述

7 总结方程得到本质矩阵E和基础矩阵F

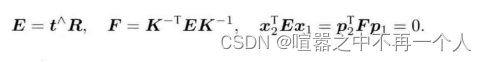
本质矩阵和基础矩阵之间只相差1个内参，只需要求解本质矩阵即可，内参一般都是已知的

2 本质矩阵E：通过本质矩阵求解R/t

几何意义：
本质矩阵是一个3x3的矩阵，用于描述两个摄像头之间的相对位置和方向。它涉及到摄像头的旋转和平移，用于将一个摄像头的点投影到另一个摄像头的图像平面上。它仅仅包含旋转和平移信息，不包含摄像头的内参（如焦距和光心）。
作用：
在SLAM系统中，当我们需要恢复场景的三维结构时，了解摄像头的相对运动是非常重要的。本质矩阵提供了一种**从两个图像中估计摄像头的相对姿态（旋转和平移）的方式。**通过本质矩阵，我们可以计算出点在两个不同视图中的对应关系，从而重建三维结构。
特点：
- 本质矩阵是一个3x3的矩阵，但它只有5个自由度（3个旋转和2个平移）。
- 由于它只描述相对运动，所以不包含尺度信息(因为是通过归一化坐标推导出来的)。
- 它是对极几何的一部分，本质矩阵中包含的信息可以用来创建对极约束，这是一种几何约束，用于找到图像之间的点对应关系。
8点法求解本质矩阵：
常见的求解本质矩阵的方法是使用八点法或五点法。这些方法基于一组点的对应关系（至少8个或5个），通过解线性方程组来计算本质矩阵。在实际应用中，为了提高精度，通常会使用RANSAC等随机抽样一致性算法来处理噪声和异常值。
通俗理解：
想象一下你用两只眼睛看同一个物体，每只眼睛看到的图像略有不同。本质矩阵就是一个工具，它告诉我们这两个视图之间的差异是如何的。具体来说，它告诉我们头部的旋转和平移是如何的。通过了解这些差异，我们可以更好地理解我们周围的三维世界。
通过本质矩阵分解求解R/t：
奇异值（SVD）分解方法
本质矩阵缺点——退化场景：

1 相机发生纯旋转：此时E的自由度会下降t为0
2 特征点在同一平面上：本质矩阵E本身不直接包含深度信息，但是它的计算和解释都依赖于3D空间中的结构和运动。
3 解决方法：使用单应矩阵

3 单应矩阵：通过单应矩阵解决退化问题

单应矩阵（Homography Matrix）：

单应矩阵是一种在计算机视觉和图像处理中常用的变换，用于描述两个平面之间的映射。它是一个3x3的矩阵，用于描述投影几何中的线性变换。它可以描述旋转、缩放、剪切和透视变换的组合。

原理：

单应矩阵H的基本原理是使用一种称为“单应性变换”或“射影变换”的方法来映射二维图像上的点。对于两个平面之间的任意点p和p’，我们有以下关系：

p’ = Hp

其中p和p’分别是在两个图像中对应的点的齐次坐标，H是单应矩阵。

作用和通俗理解：

单应矩阵用于描述在射影变换下，一个平面上的点如何映射到另一个平面上。通俗地说，你可以想象单应矩阵是描述如何从一个平面（如一张图片）到另一个平面（如另一张图片）的“变形规则”。这种变形可以包括旋转、缩放、剪切和透视变换。

在日常生活中，单应变换的一个常见例子就是在不同的视角下看同一张图片。例如，当你从不同的角度看一张贴在墙上的画时，画的形状和大小可能会变，但它们之间的关系可以由单应矩阵来描述。

应用范围：

单应矩阵在计算机视觉和图像处理中有广泛的应用，例如：

图像配准和拼接：当我们需要将多张图片拼接在一起以创建全景图时，可以使用单应矩阵来对齐图像。
增强现实：在增强现实中，我们可以使用单应矩阵将虚拟物体正确地投影到真实世界的图像上。
3D重建：在从多视图图像进行3D重建时，单应矩阵可以描述相邻图像之间的关系。

单应矩阵和本质矩阵的关系：

单应矩阵和本质矩阵都是描述图像之间关系的工具，但它们的使用场景和所包含的信息是不同的。

本质矩阵E描述的是两个相机视图之间的相对旋转和平移，适用于场景中的3D点在两个相机视图之间的变换，尤其是当两个相机有相对运

动时。本质矩阵不包含尺度信息，只能恢复到除了尺度之外的相机运动。

单应矩阵H则是描述两个平面之间的映射，适用于所有点都在同一个平面上的情况，比如地面、墙面等。单应矩阵能够描述更广泛的变换，包括旋转、平移、缩放和透视等。

总的来说，单应矩阵和本质矩阵都是在计算机视觉中描述图像间关系的重要工具，但它们的适用场景和提供的信息有所不同。在实际应用中，我们需要根据具体的任务和场景选择合适的工具。

获得地图点（通过R/t求解）

单目相机无法获取空间点的深度信息只是通过归一化坐标求得的旋转和平移，其平移t也缺失一个深度信息，而地图的构建必须要获得深度信息。

方法：

1、三角测距

原理：
三角测距法的基本原理源于几何学中的三角形性质。给定一个三角形，如果我们知道一个边长（通常称为基线）和与这个边相对的两个角度，我们可以利用三角形的性质来计算其他两个边的长度。在计算机视觉中，我们通常使用两个相机的位置作为基线，并且使用每个相机观察到的角度来计算3D点的深度。
推导公式：
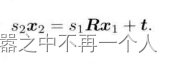
特点：
1、需要相机有一个位移（视差）纯旋转不行
2、视差太小，会导致像素匹配不准，则会导致误差大
3、视差太大，像素不确定性小，深度误差也会小，但是会丢失部分匹配特征