1.简介

主要内容：

1. 对SLAM中常见的相机模型进行介绍，包括针孔相机模型和鱼眼相机模型
2. 对每种相机模型的畸变模型进行介绍
3. 对VSLAM中常见的几种去畸变方法进行介绍
4. 对常见的几种相机标定方法进行总结

对于VSLAM来说关于相机投影模型和畸变模型暂时不需要了解过于深入，通常来说在VSLAM领域相机的投影模型主要分为针孔模型(Pinhole)和全向模型(Omni)两种，相机的畸变模型分为切向径向畸(RanTan)和等距畸变(Equidistant,EQUI)两种，也是ORBSLAM3中针对针孔相机和鱼眼相机使用的两种畸变模型。

每种相机模型又可以和畸变模型互相搭配，并对不同的搭配方式进行了命名：

• MEI Camera: Omni + RanTan
• Pinhole Camera: Pinhole + Rantan

下面将挨个对上述投影模型和畸变模型原理进行介绍。

参考链接：
[1]相机的成像模型(Pinhole + Omni)和畸变模型(RanTan, FOV, EQUI)

2 针孔相机投影模型和畸变模型

2.1 针孔相机投影模型

针孔相机投影模型本质上是根据小孔成像原理，基于相似三角形关系计算得到3D空间点在成像平面的坐标，通过将坐标系进行相应的平移和缩放，最终得到像素平面坐标。

设O-x-y-z为相机坐标系，习惯上将z轴指向相机前方,x轴向右，y轴向下，O为摄像机的光心也是针孔模型中的针孔。现实世界的点P，经过小孔O投影后，落在物理成像平面O'-x'-y'上，成像点为P’。

世界坐标系中三维点 $P={\left[X,Y,Z\right]}^T$ 和像素坐标系中二维点 $p={\left[u,v\right]}^T$ 的关系为：
$$s\tilde{p}=A\left[Rt\right]\tilde{P}$$
其中, $s$ 为缩放因子(即 $Z_c$ ),A为相机内参矩阵，${\left[R,t\right]}^T$ 为相机外参矩阵,$\tilde{m}$和$\tilde{M}$表示分别为m和M对应的齐次坐标系。

详细过程为：

1.世界坐标系到相机坐标系

2.相机坐标系到成像坐标系
根据三角形相似关系有：

整理得：

3.成像坐标系到像素坐标系

像素坐标系通常的定义方式是：原点o'位于图像的左上角，u轴向右与x轴平行，v轴向下与y轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的位移。我们设像素坐标在u轴上缩放了α倍，在v轴上缩放了β倍。同时，原点平移了 ${\left[c_x,c_y\right]}^T$ 。那么整理得，坐标之间的关系为：

其中，

• f为镜头焦距，单位为米
• α和β的单位为像素/米
• fx,fy为x,y方向的焦距，单位为像素

最终，写成矩阵的形式为：

2.2 针孔相机畸变模型

普通相机畸变通常包括径向畸变和切向畸变，如下图所示：

切向畸变表达式沿半径方向的偏移量，径向畸变的形成原因是镜头制造工艺不完美，使得镜头形状存在缺陷，通常又分为桶性畸变和枕形畸变，表现在dr上即往图像的外面偏和往图像里面偏。
${\left[x_{distorted},y_{distorted}\right]}^T$ 是畸变后点的归一化坐标。

2.2.1 径向畸变

真实的摄像头使用的并不是针孔，它们使用的是能一次性聚焦大量光线的镜头，这使得其能迅速生成图像，但是，镜头仍会产生失真，光线通常会在摄像机镜头的边缘出现较大或较小幅度的弯曲，这会产生图像边缘扭曲的效果，因此，线条或者物体会比真实情况呈现出或多或少的弯曲。这种失真被称为径向畸变，是最常见的失真类型。

实际情况中我们常用r = 0处的泰勒级数展开的前几项来近似描述径向畸变，径向畸变后的归一化坐标为：

2.2.2 切向畸变

切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致（相机的组装过程中由于不能使得透镜和成像面严格平行），切向畸变需要两个额外的畸变参数来描述，切向畸变后的归一化坐标为：

其中，$r^2=x^2+y^2$

对于相机坐标系中的一点P，我们能够通过5个畸变系数找到这个点在像素平面上的正确位置：

由于参数过多导致数值求解不稳定, 通常只使用$k_1,k_2,k_3,k_4,k_5$ 。综上，我们一共需要5个畸变参数$\left(k_1,k_2,k_3,k_4,k_5\right)$ 来描述透镜畸变。将畸变后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置：

2.3 针孔相机投影过程总结

3.全向相机模型

参考链接：
[1]相机模型-Unified Camera Model

全向相机模型又被称为统一相机模型(UNIFIED PROJECTION MODEL),因为它既可以表示一般针孔相机投影过程，也可以表示广角相机(鱼眼相机)的投影模型。这个模型的本质其实是将原始的光心在光轴方向上进行移动，得到一个虚拟的光心，从而达到模拟畸变的目的。用这个模型可以模拟针孔相机的成像过程，也可以模拟广角以及鱼眼相机的成像过程。需要注意的是，在广角或鱼眼相机中，该模型不会完全模拟畸变过程，所以还需要搭配一些其他畸变模型，比如 相机模型–针孔相机投影（pinhole camera model）中讲的Brown畸变模型。

3.1 广角相机介绍

广角相机(omnidirectional camera)： 有360度视野的相机，或视野能覆盖半个球或近似整个球的相机。根据镜头聚光方式的不同可以分为以下三种：

1. Dioptric cameras：一组shaped lenses，如鱼眼镜头，可以得到大于180度视野；通过透镜来实现, 主要是折射。
2. Catadioptric cameras：一个标准相机和一个面镜，在水平面可以提供360度视野，仰角方向大于100度；
3. polydioptric camera：组合多个相机来重叠相机视野。
   

3.2 全向相机投影模型

接下来结合示意图对投影模型进行详细说明。假设相机坐标系下的3D空间点$P=\left(x,y,z\right)$,将其归一化到以相机光心为中心的单位球面上$P_s=\left(x_s,y_s,z_s\right)$.若无畸变的情况下，可以直接得到归一化坐标$p=\left(\frac{x_s}{z_s},\frac{y_s}{z_s},1\right)$,在有畸变的情况下，可以找到一个以虚拟光心(与原光心只存在光轴上的平移，设平移量为ξ)为原点的虚拟相机坐标系，那么此时$P_s$在虚拟相机坐标系下的坐标变为$\left(x_s,y_s,z_s+\xi \right)$,投影到成像平面中可以得到畸变后的归一化坐标$p_d=\left(\frac{x_s}{z_s+\xi },\frac{y_s}{z_s+\xi },1\right)$。

1. 设相机坐标系下的3D空间点$P=\left(x,y,z\right)$,将其归一化到以相机为光心的单位球面上$P_s=\left(x_s,y_s,z_s\right)=\left(\frac{x_c}{\Vert P_c\Vert },\frac{y_c}{\Vert P_c\Vert },\frac{z_c}{\Vert P_c\Vert }\right)$.
2. 转换到虚拟成像平面上可以得到$p=\left(x_p,y_p,1\right)=\left(\frac{x_s}{z_s+\xi },\frac{y_s}{z_s+\xi },1\right)$.
3. 对p添加畸变(如针孔相机畸变模型)，得到包含畸变的归一化坐标$p_d=\left(x_d,y_d,1\right)$.
4. 根据针孔模型可以到像素坐标$u=f_x{x}_d+c_x,v=f_y{y}_d+c_y$.

3.3 全向相机反投影模型

反投影就是已知图像平面的一点$p_{uv}=\left(u,v\right)$求解得到相机坐标系下的坐标$P_c$或者单位球坐标

1. 设图像上存在某个点$p=(u,v)$.
2. 根据内参得到归一化平面坐标$p_d=\left(\frac{u-c_x}{fx},\frac{v-c_y}{fy},1\right)$.
3. 根据畸变模型进行去畸变处理，得到畸变前的归一化坐标$p_{ud}=\left(x_{ud},y_{ud},1\right)$.
4. 将归一化坐标转换到相机坐标系下$P_c=\left(x_{ud},y_{ud},1-\frac{\xi \left(r^2+1\right)}{\xi +\sqrt{1+r^2\left(1-{\xi }^2\right)}}\right)$
5. 将相机坐标系坐标转换为单位球坐标.

对于第4步相机坐标系3D点的z值计算过程如下：
对于上述全向相机投影模型图示，可以假设$O{P}_s$上存在一点$P^{\prime }=\left(x_d,y_d,z^{\prime }\right)$,将其归一化后就是$P_s$,可见$P^{\prime }$和$P_s$对应同一像素点。按照上述投影过程可以得到$p_d$,即：
$$\left(\frac{x_d}{z^{\prime }+\xi \sqrt{z^{\prime 2}+r^2}},\frac{y_d}{z^{\prime }+\xi \sqrt{z^{\prime 2}+r^2}},1\right)=\left(x_d,y_d,1\right)$$

从而：
$$z^{\prime }+\xi \sqrt{z^{\prime 2}+r^2}=1$$

解得：
$$z^{\prime }=\frac{\xi \sqrt{1+r^2(1-{\xi }^2)}-1}{{\xi }^2-1}$$

4.常见去畸变方法

4.1 基于Opencv的去畸变方法

1. 直接对整副图像进行remap
   对图像进行remap的操作在ros节点中实现，首先将带有畸变信息的图像根据标定的参数对整副图像进行映射得到去畸变后的图像，然后再送入SLAM系统。

对于EuRoC这种图像带有畸变信息的数据集，一般采用该操作。对于zed,Realsense相机以及kitty数据集，图像本身是已经矫正过得，无需去畸变操作。

2. 只对特征点进行去畸变
   ORBSLAM3中对特征点去畸变在构造Frame时完成，基于OpenCV函数cv::undistortPoints()实现，关键部分代码如下：

// 将mat变为N行4列，前两列为含有畸变的坐标，后两列为对应去畸变坐标
mat=mat.reshape(2);
// 参数依次为：输入矩阵，输出矩阵，相机内参矩阵，畸变系数，R参数是用在双目里的单目里置为空矩阵，相机内参 
cv::undistortPoints(mat,mat, static_cast<Pinhole*>(mpCamera)->toK(),mDistCoef,cv::Mat(),mK);
mat=mat.reshape(1);

4.2 逐渐逼近式去畸变方法

参考链接：https://blog.csdn.net/qq_33733356/article/details/124356158
畸变的程度越靠近图像边缘越高，这点是VINS中去畸变的主要依据思想。VINS采用一种逐渐逼近式去畸变方法.

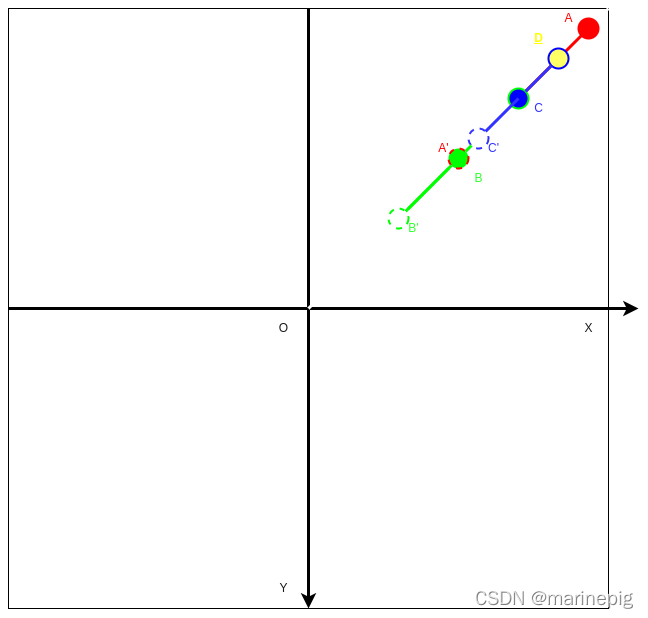
根据畸变强度越靠近图像边缘越大 AA’ > BB’ > CC’

已知含有畸变的A'坐标，需要求出发生畸变前的真实坐标A
根据畸变公式可以由真实坐标得到包含畸变坐标是比较容易计算的，反之要复杂很多。
因此VINS中将已知的A'当做真实的坐标B，通过畸变公式得到畸变后的B'。得到畸变强度（近似表示）BB'，从A'移动BB'，得到更加靠近A的C点。然后以C继续推导出更靠近A点的D。反复迭代，即可得到在接受范围内无限靠近A的点。

5.常见相机标定方法和标定工具

目前使用过的相机标定工具主要有以下几种：

1. Kalibr工具
2. 基于Opencv的标定
3. 基于ROS的标定

目前来说基于ROS的标定感觉效果最好，可以实现单目和双目相机的标定。

对于相机和IMU的联合标定可以使用Kalibr工具，或者使用港科大imu_utils工具标定好IMU数据再进行联合标定。

参考链接：
[1]使用kalibr标定工具进行单目相机和双目相机的标定
[2]基于opencv进行双目相机的标定
[3]相机和IMU联合标定参考链接notes
[4]ROS下采用camera_calibration进行单目相机标定
[5]ROS下采用camera_calibration进行双目相机标定