线性规划：定义：¹

线性规划（Linear programming,简称LP），是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，是辅助人们进行科学管理的一种数学方法，是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。

线性规划是运筹学的一个重要分支，广泛应用于军事作战、经济分析、经营管理和工程技术等方面。为合理地利用有限的人力、物力、财力等资源作出的最优决策，提供科学的依据。

建模流程²

1. 理解要解决的问题，目标及限制条件
2. 定义决策变量(x1, x2, …, xn)，每一组值表示一个方案。
3. 用决策变量的线性函数形式写出目标函数，确定最大化目标或最小化目标。
4. 用一组决策变量的等式或不等式表示解决问题过程中必须遵循的约束条件。

目标函数：Max(Min)z=c1x1+c2x2+…+cnxn
约束条件：
a11x1+a12x2+…+a1nxn≤b1
a21x1+a22x2+…+a2nxn≤b2
am1x1+am2x2+…+amnxn≤bm
x1，x2，…，xn≥0，bi≥0

python模块

使用python工具包：from scipy.optimize import linprog

def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)

变量解释：

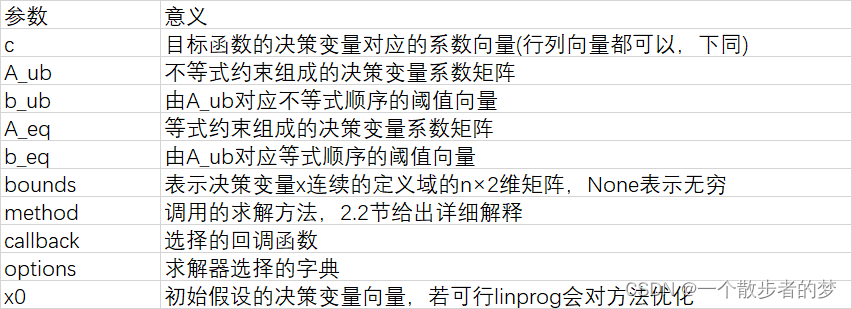
Python的SciPy库中的linprog函数是用来解决最小化问题的，因此，对于最大化问题，有必要对原始目标函数进行转换。通过将目标函数的系数乘以-1（改变其符号），可以将最小化问题转化为一个最大化问题。

案例

工厂生产产品1和产品2，产品1每台获利50元，产品2每台获利100块，资源限制产品1+产品2总共不超过300台；材料A不超过400千克，材料B不超过25千克；问：产品1和产品2分别生产多少台获利最大？

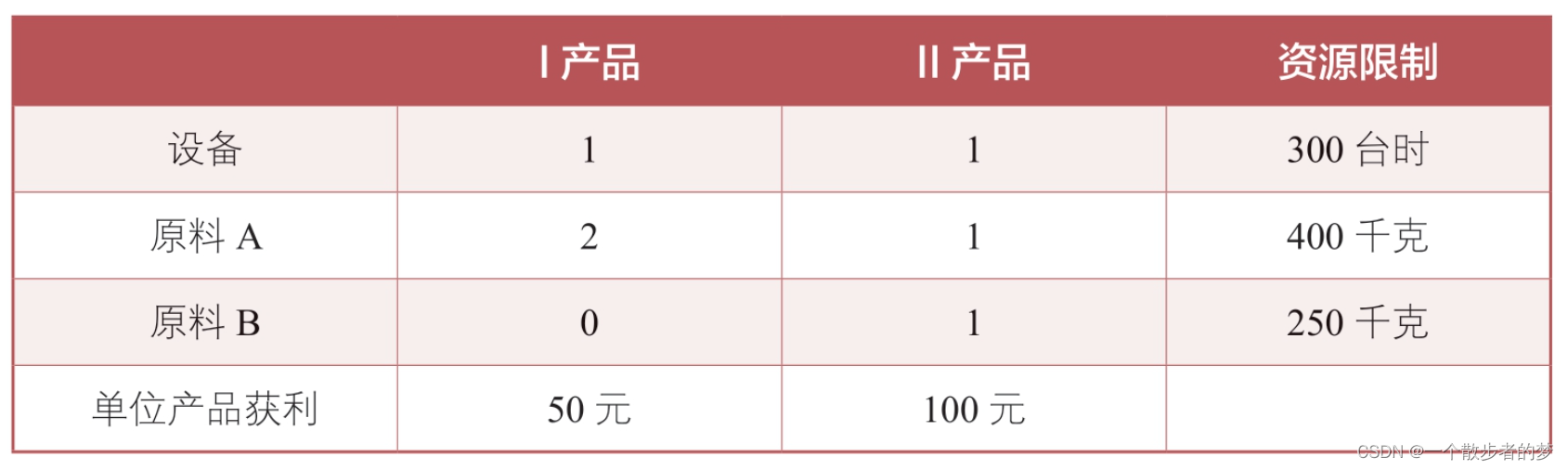
目标函数（获利）：
maxz = 50 * x1 + 100 * x2

限制条件：
x1 + x2 <= 300
2 * x1 + x2 <= 400
x2 <= 250(0x1 + 1x2<=250)
x1 > 0 (1x1 + 0x2>0)
x2 > 0 (0x1 + 1x2>0)

python求解：

from scipy.optimize import linprog
import numpy as np

a = np.array([[1,1],[2,1],[0,1],[-1,0],[0,-1]])
b = np.array([300,400,250,0,0])
c = np.array([-50,-100])
res = linprog(c,A_ub=a,b_ub=b)
print(res)

fun为最优解，因为求的最小值，-x1-x2<=-27499，翻转过来：x1+x2>=27499，即最优解为27500，产品1个数50，产品2个数250台；

---

1. 百度百科-线性规划定义 ↩︎

2. 《商业策略数据分析》 ↩︎