算法题之数字处理
- 一、统计各位数字之和为偶数的整数个数
- 1.1、题目
- 1.2、理解题目
- 1.3、解题思路(暴力枚举)
- 1.4、解题思路2(数学公式)
- 1.5、小结
- 二、替换空格
- 2.1、题目
- 2.2、解题:遍历原地修改
- 三、旋转数组的最小数字
- 3.1、题目
- 3.2、思路
- 3.3、代码实现
- 3.4、小结
- 总结
一、统计各位数字之和为偶数的整数个数
1.1、题目
给你一个正整数 num ,请你统计并返回 小于或等于 num 且各位数字之和为 偶数 的正整数的数目。
正整数的 各位数字之和 是其所有位上的对应数字相加的结果。
示例 1:
输入:num = 4
输出:2
解释:
只有 2 和 4 满足小于等于 4 且各位数字之和为偶数。
示例 2:
输入:num = 30
输出:14
解释:
只有 14 个整数满足小于等于 30 且各位数字之和为偶数,分别是:
2、4、6、8、11、13、15、17、19、20、22、24、26 和 28 。
来源:力扣(LeetCode)
1.2、理解题目
也就是给一个int型的整数num,统计大于0小于num范围内的满足要求的数字个数,这个数字的要求是其各位数字之和为偶数(比如10的个位数之和为1+0=1,不满足要求;13的个位数之和为1+3=4,满足要求)。
1.3、解题思路(暴力枚举)
首先想到的解题思路:
将num逐步减一(满足小于或等于 num要求),用一个循环对当前值的计算值取模和求余(,每次的取模得到的数(就是各位数)相加,直到求余得到的数为0时退出循环,然后判断取模得到的数(就是各位数)相加是否为偶数。
代码:
class Solution {
public:
int countEven(int num) {
int count=0;//统计数量
while(num>1)// 判断
{
int pre=num;// 保存要计算的数值
int cur=0; // 记录
while(pre)
{
cur+=pre%10;//取模并相加
pre/=10;//取余
}
if(cur%2==0)//偶数
count++;//统计
num--;//递减
}
return count;
}
};
测试结果:
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:5.8 MB, 在所有 C++ 提交中击败了40.59%的用户
通过测试用例:71 / 71
时间复杂度: O(n log n) 。
空间复杂度: O(1)。
1.4、解题思路2(数学公式)
首先,位于区间[0, 10)的奇数和偶数的个数都是5个。将 num表示为 10y+x的形式,其中 x大于等于0小于10且y大于等于0 ,那么位于区间 [0,num]的整数可以分为两个部分:区间[10y+0,10y+x]和区间[0,10y+0]
。
总结就是一个公式:将 num表示为10y+x,y=num/10,x=num%10;然后计算y的各个数之和是否为偶数,如果是偶数则结果为 y5+x/2+1 ,如果是奇数则结果为 y*5+(x+1)/2 。
上述区间中多计入了整数0,因此结果应该是位于上述区间且各位数字之和为偶数的个数减1。
class Solution {
public:
int countEven(int num) {
// num=10*y+x
int y=num/10;
int x=num%10;
int res=y*5;
int ysum=0;
while(y)
{
ysum+=y%10;
y=y/10;
}
if(ysum%2==0)
res+=x/2+1;
else
res+=(x+1)/2;
return res-1;
}
};
测试结果:
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:5.8 MB, 在所有 C++ 提交中击败了30.07%的用户
时间复杂度: O(log n)。
空间复杂度:O(1)。
1.5、小结
暴力枚举各位数之和的核心:
while(...){
sum+=num%10;
num/=10;
}
- 数学公式: num表示为10y+x , y=num/10,x=num%10 。result=y5+(y的各位数之和是偶数吗)?(x/2+1) : (x(+1)/2) -1 。
二、替换空格
2.1、题目
实现一个函数,把字符串s中的每个空格替换成"%20"。
示例 1:
输入:s = “We are happy.”
输出:“We%20are%20happy.”
来源:力扣(LeetCode)
2.2、解题:遍历原地修改
在 C++ 语言中, string 被设计成「可变」的类型,因此可以在不新建字符串的情况下实现原地修改。
class Solution {
public:
string replaceSpace(string s) {
int len=s.length();
string ret="";
int i=0;
while(i<len)
{
if(s[i]==' ')
ret+="%20";
else
ret+=s[i];
i++;
}
return ret;
}
};
时间复杂度 O(N) 。
空间复杂度 O(1) 。
三、旋转数组的最小数字
3.1、题目
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
示例 1:
输入:numbers = [3,4,5,1,2]
输出:1
示例 2:
输入:numbers = [2,2,2,0,1]
输出:0
来源:力扣(LeetCode)
3.2、思路
排序数组的查找问题首先考虑使用二分法解决,其可将遍历法的线性级别时间复杂度降低至对数级别。
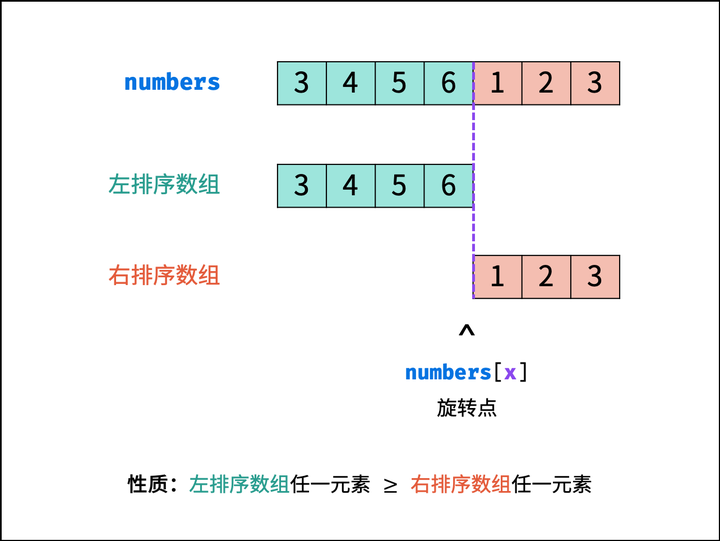
二分法算法流程:
- 初始化:声明两个指针low、hight分别指向numbers的首元素和尾元素。
- 使用一个循环来二分,每次循环都计算中心位置inv=low+(hight-low)/2。
- 调整low和hight的位置:如果中心点inv位置的元素小于最高点hight位置的元素,则hight=inv;如果中心点inv位置的元素大于最高点hight位置的元素,则low=inv+1;否则hight=hight+1。
- 返回值: 当low==hight时跳出二分循环,并返回 旋转点的值 nums[low] 即可。
3.3、代码实现
class Solution {
public:
int minArray(vector<int>& numbers) {
int hight=numbers.size()-1;
int low=0;
while(low<hight)
{
int inv=low+(hight-low)/2;
if(numbers[inv]>numbers[hight])
{
low=inv+1;
}
else if(numbers[inv]<numbers[hight])
{
hight=inv;
}
else
hight-=1;
}
return numbers[low];
}
};
时间复杂度 O ( l o g 2 N ) O(log_2 N) O(log2N) : 在特例情况下(例如 [1, 1, 1, 1]),会退化到 O(N)。
空间复杂度 O(1) : 变量使用常数大小的额外空间。
当然,还有暴力枚举法,这种方法不建议。
class Solution {
public:
int minArray(vector<int>& numbers) {
int n=numbers.size();
if(n==0)
return 0;
int res=numbers[0];
for(int i=1;i<n;i++)
{
if(numbers[i]<numbers[i-1])
return numbers[i];
}
return res;
}
};
3.4、小结
二分法可以解决排序数组的查找问题,降低时间复杂度。
二分法步骤:
- 初始化:定义两个指针low、hight,分别指向开头和末尾。
- 循环二分:每次循环都计算中间点(hight-low)/2,根据题意比较中心点和边沿的关系进行low和hight的变化。
- 当low==hight时跳出二分循环,并返回low对应的结果即可。
总结
一定要做好总结,特别是当没有解出题来,没有思路的时候,一定要通过结束阶段的总结来反思犯了什么错误。解出来了也一定要总结题目的特点,题目中哪些要素是解出该题的关键。不做总结的话,花掉的时间所得到的收获通常只有 50% 左右。
在题目完成后,要特别注意总结此题最后是归纳到哪种类型中,它在这种类型中的独特之处是什么。