力扣动态规划专题（六）编辑距离与回文问题 步骤及C++实现

news2024/11/8 0:43:20

文章目录

  • 392. 判断子序列
    • 动态规划
    • 双指针
  • 115.不同的子序列
  • 583. 两个字符串的删除操作
    • 方法一
    • 方法二
  • 72. 编辑距离
  • 647. 回文子串
    • 动态规划
    • 双指针
  • 516.最长回文子序列

392. 判断子序列

在这里插入图片描述

动态规划

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度。判断s是否为t的子序列。即t的长度是大于等于s的

  2. 确定递推公式
    和题1143一样，不同的是只有t可以删除元素，1143题两个字符串都可以删除元素

  • t中找到一个在s中有的字符，if (s[i - 1] == t[j - 1])，相当于t要删除元素，继续匹配，dp[i][j] = dp[i - 1][j - 1] + 1;
  • t中没有找到s中有的字符，if (s[i - 1] != t[j - 1])，相当于t要删除元素，如果删除当前元素t[j - 1]，那么dp[i][j]的数值就是看s[i - 1]与 t[j - 2]的比较结果了，dp[i][j] = dp[i][j - 1];

  1. dp数组如何初始化
    dp[i][j]依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，dp[0][0]和dp[i][0]都要初始化的，dp[i][0] 表示以下标i-1为结尾的字符串与空字符串的相同子序列长度，所以dp[i][0]=0，同理dp[0][j]=0。
    和题718一样，如果dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，需要对第一行和第一列单独初始化，dp[i][0]=1，dp[0][j]=1

  2. 确定遍历顺序
    dp[i][j]依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，遍历顺序从上到下，从左到右

  3. 举例推导dp数组
    以示例一为例，输入：s = “abc”, t = “ahbgdc”，如果过dp[s.size()][t.size()] 与 字符串s的长度相同说明：s与t的最长相同子序列就是s，s 就是 t 的子序列

  4. C++实现
    时间复杂度mn，时间复杂度mn

class Solution {
public:
    bool isSubsequence(string s, string t) {
        //动态规划
        vector<vector<int>> dp(s.size()+1, vector<int>(t.size()+1, 0));
        for(int i=1; i<=s.size(); i++)
        {
            for(int j=1; j<=t.size(); j++)
            {
                if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = dp[i][j-1];
            }
        }
        if(dp[s.size()][t.size()] == s.size()) return true;
        return false;
    }
};

双指针

两个指针i和j分别指向s和t的起始位置，如果s[i]==t[j]，双指针同时后移；如果不相等，i不移动，j后移。如果i到达s的末尾，说明s是t的子序列。
时间复杂度n，空间复杂度1

class Solution {
public:
    bool isSubsequence(string s, string t) {
        //双指针
        int i=0, j=0;
        for(; i<s.size() && j<t.size(); j++)
        {
            if(s[i] == t[j]) i++;
        }
        //if(i == s.size()) return true;
        return i == s.size();
    }
};

115.不同的子序列

在这里插入图片描述

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数

  2. 确定递推公式
    1）如果s[i - 1] = t[j - 1]，dp[i][j]可以有两部分组成。

  • 用s[i - 1]来匹配，个数为dp[i - 1][j - 1]，即不需要考虑当前s子串和t子串的最后一位字母，只需要 dp[i-1][j-1]
  • 不用s[i - 1]来匹配，个数为dp[i - 1][j]
  • 例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的。不用s[3]来匹配的话就是用s[0]s[1]s[2]组成的bag，用s[3]来匹配的话就是s[0]s[1]s[3]组成的bag。所以，if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

2）如果s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成

  • 不用s[i - 1]来匹配，相当于模拟在s中删除这个元素，if(s[i - 1] != t[j - 1]) dp[i][j] = dp[i - 1][j];
  • 注意题目求的是 s 中有多少个 t，而不是t中有多少个s，所以只考虑 s中删除元素的情况，故不用s[i - 1]来匹配 的情况。
  1. dp数组如何初始化
  • dp[i][0]：以i-1为结尾的s出现空字符串的个数，s删除所有元素出现空字符串的个数只能是1，dp[i][0]=1
  • dp[0][j]：空字符串s出现以j-1为结尾的字符串t的个数，s子序列不可能组成t，dp[0][j]=0，
  • dp[0][0]：空字符串s，可以删除0个元素，变成空字符串t，dp[0][0]=1

  1. 确定遍历顺序
    dp[i][j]依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，遍历顺序从上到下，从左到右

  2. 举例推导dp数组
    输入，s：“baegg”，t：“bag”

  3. C++实现

class Solution {
public:
    int numDistinct(string s, string t) {
        //三种情况初始化 dp[0][0] dp[i][0] dp[0][j]
        //s匹配t  dp[i][j] 以i-1为结尾的s子序列中出现以j-1为结尾的t的个数

        vector<vector<uint64_t>> dp(s.size()+1, vector<uint64_t>(t.size()+1));//不能用int
        for(int i=0; i<s.size(); i++) dp[i][0] = 1;//初始化 dp[0][0] dp[i][0]
        for(int j=1; j<t.size(); j++) dp[0][j] = 0;//初始化dp[0][j]
        //dp
        for(int i=1; i<=s.size(); i++)
        {
            for(int j=1; j<=t.size(); j++)
            {
                //s匹配t s:bagg t:bag s[0]s[1]s[2]或者s[0]s[1]s[3] 组成t
                if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                else dp[i][j] = dp[i-1][j];
            }
        }
        return dp[s.size()][t.size()];
    }
};

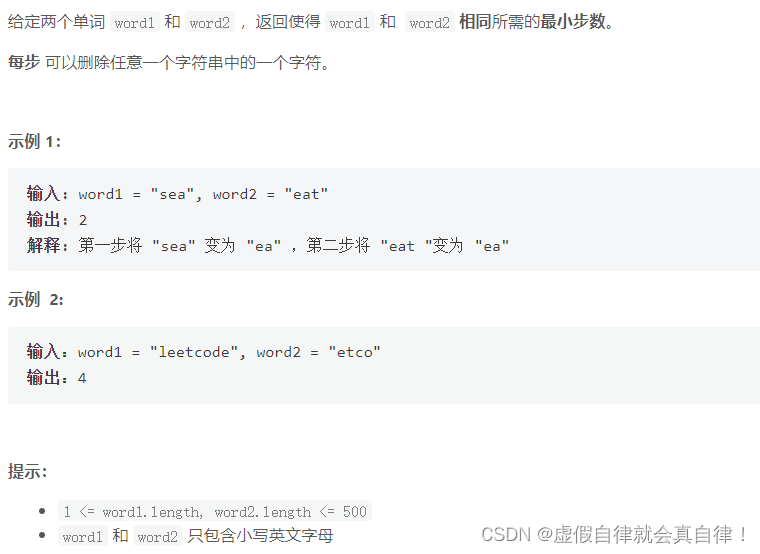
583. 两个字符串的删除操作

在这里插入图片描述

方法一

和题115思路一致，两个字符串都可以删除操作。

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，达到相等需要删除元素的最少次数。

  2. 确定递推公式
    1）if(word1[i - 1] == word2[j - 1])，dp[i][j] = dp[i - 1][j - 1];

2）if(word1[i - 1] != word2[j - 1])，dp[i][j]有三种情况

  • 情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
  • 情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
  • 情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
  • 最少删除次数，取最小值，dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});。
  • dp[i][j-1]是以i-1为结尾的字符串word1和以j-2位结尾的字符串，不考虑word2[j - 1]，那么在dp[i][j-1]基础上再删除 word1[i - 1]，相当于同时删除word1[i - 1]和word2[j - 1]，即dp[i][j-1] + 1 = dp[i - 1][j - 1] + 2，递推公式简化dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);。

  1. dp数组如何初始化
    dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除i个元素才能和word2相等，因此dp[i][0] = i。同理，dp[0][j] = j

  2. 确定遍历顺序
    dp[i][j]依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，遍历顺序从上到下，从左到右

  3. 举例推导dp数组
    输入，word1:“sea”，word2:“eat”

  4. C++实现

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1));
        //初始化
        for(int i=0; i<=word1.size(); i++) dp[i][0] = i;
        for(int j=0; j<=word2.size(); j++) dp[0][j] = j;
        //dp数组更新
        for(int i=1; i<=word1.size(); i++)
        {
            for(int j=1; j<=word2.size(); j++)
            {
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1);
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

方法二

和题1143.最长公共子序列一样，只要求出两个字符串的最长公共子序列长度即可。除了最长公共子序列，其他字符都是必须删除的，用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

class Solution {
public:
    int minDistance(string word1, string word2) {
        //方法2
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));
        for(int i=1; i<=word1.size(); i++)
        {
            for(int j=1; j<=word2.size(); j++)
            {
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return word1.size()+word2.size() - dp[word1.size()][word2.size()]*2;
    }
};

72. 编辑距离

在这里插入图片描述

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离

  2. 确定递推公式
    1）if(word1[i - 1] == word2[j - 1])，字符相同，不操作，dp[i][j] = dp[i - 1][j - 1];

2）if(word1[i - 1] != word2[j - 1])，字符不同，插入、删除、替换三种操作

  • 操作一：word1删除一个元素，相当于是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离dp[i - 1][j] 加一个操作，最少操作次数为：dp[i][j] = dp[i - 1][j] + 1;
  • 操作二：word1删除一个元素，同理dp[i][j - 1]加一个操作，最少操作次数为：dp[i][j] = dp[i][j - 1] + 1;
  • 操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同。此时相当于字符相同时不操作，那么在此基础上再加一次替换操作即可，dp[i][j] = dp[i - 1][j - 1] + 1;
  • 添加元素相当于删除元素，例如word1 = “ad” ，word2 = “a”，word1删除元素’d’ 和 word2添加一个元素’d’，变成word1=“a”, word2=“ad”， 最终的操作数是一样的。
    因此，当 if (word1[i - 1] != word2[j - 1]) 时，最小的操作数为：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

  1. dp数组如何初始化
    dp[i][0]表示以下标i-1为结尾的字符串word1和空字符串word2的最近编辑距离。相当于把word1里的元素全部删除，dp[i][0] = i;。同理，dp[0][j] = j;

  2. 确定遍历顺序

  • dp[i][j] = dp[i - 1][j - 1]
  • dp[i][j] = dp[i - 1][j - 1] + 1
  • dp[i][j] = dp[i][j - 1] + 1
  • dp[i][j] = dp[i - 1][j] + 1
    从递推公式来看，有四个推导公式，也就是有三个方向可以推出dp[i][j]，所以要从前向后，从上到下来遍历

  1. 举例推导dp数组
    以示例1为例，输入：word1 = “horse”, word2 = “ros”

  2. C++实现

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));
        //初始化 dp[i][0] dp[0][j]
        for(int i=0; i<=word1.size(); i++) dp[i][0] = i;
        for(int j=0; j<=word2.size(); j++) dp[0][j] = j;
        //dp数组更新
        for(int i=1; i<=word1.size(); i++)
        {
            for(int j=1; j<=word2.size(); j++)
            {
                if(word1[i-1] ==word2[j-1]) dp[i][j] = dp[i-1][j-1];//字符相同不操作
                //字符不相同 替换dp[i - 1][j - 1] + 1
                //或者 删word1 dp[i-1][j]+1
                //或者 删word2 dp[i][j-1]+1
                else dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

647. 回文子串

在这里插入图片描述

动态规划

时间、空间复杂度：O(n^2)

字符串s=“cbabc”， 如果s[1]、s[2]、s[3]组成的字符串是回文，那么进一步要判断s[0]与s[4]是否相等，如果相等，s就是回文字符串。

步骤

  1. 确定dp数组以及下标的含义
    布尔类型的dp[i][j]：表示左闭右闭区间范围[i,j]的子串是否为回文子串，如果是，dp[i][j]为true，否则为false。

  2. 确定递推公式
    1）s[i]与s[j]不相等，dp[i][j]一定是false。
    2）s[i]与s[j]相等时，有如下三种情况

  • 情况一：下标i 与 j相同，同一个字符，例如a，回文子串
  • 情况二：下标i 与 j相差为1，例如aa，回文子串
  • 情况三：下标i 与 j相差大于1时，例如cabac，此时s[i]与s[j]都是“c”，再看[i, j]区间是不是回文子串，也就是看aba是否为回文。aba的区间[i+1, j-1]是否为回文，就看dp[i + 1][j - 1]是否为true。

  1. dp数组如何初始化
    dp[i][j]初始化为false

  2. 确定遍历顺序
    情况三中dp[i][j]依赖于dp[i + 1][j - 1]，dp[i + 1][j - 1] 在 dp[i][j]的左下角，所以从下到上，从左到右遍历

  3. 举例推导dp数组
    输入：“aaa”，j一定是大于等于i的，那么在填充dp[i][j]的时候一定是只填充右上半部分

  4. C++实现

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));//包括初始化
        int result = 0;
        for(int i=s.size()-1; i>=0; i--)
        {
            for(int j=i; j<s.size(); j++)
            {
                if(s[i] == s[j])
                {
                    if(j - i <= 1)//情况1 2
                    {
                        result++;
                        dp[i][j] = true;
                    }
                    else if(dp[i+1][j-1])//情况3
                    {
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
};

优化

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));//包括初始化
        int result = 0;
        for(int i=s.size()-1; i>=0; i--)
        {
            for(int j=i; j<s.size(); j++)
            {
                if(s[i] == s[j] && (j - i <= 1 || dp[i+1][j-1]))
                {
                        result++;
                        dp[i][j] = true; 
                }
            }
        }
        return result;
    }
};

双指针

时间复杂度：O(n^2)，空间复杂度：O(1)

class Solution {
public:
    int countSubstrings(string s) {
        //双指针
        int result = 0;
        for(int center=0; center<2 * s.size() - 1; center++)
        {
            int left = center / 2;
            int right = left + center % 2;
            while(left>=0 && right<s.size() && s[left]==s[right])
            {
                left--;
                right++;
                result++;
            }
        }
        return result;
    }
};

516.最长回文子序列

在这里插入图片描述

回文子串是要连续的，回文子序列不是连续的

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度

  2. 确定递推公式

  • 如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;
  • 如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
  • 加入s[j]的回文子序列长度为dp[i + 1][j]，加入s[i]的回文子序列长度为dp[i][j - 1]。那么dp[i][j]取最大的长度，dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

  1. dp数组如何初始化
    从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出，递推公式是计算不到 i == j的情况，需要手动初始化。当i与j相同时，dp[i][j]=1，一个字符的回文子序列长度就是1。其他情况dp[i][j]初始为0。

  2. 确定遍历顺序
    dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，从下到上，从左向右遍历。

  3. 举例推导dp数组
    输入s:“cbbd”

  4. C++实现

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for(int i=0; i<s.size(); i++) dp[i][i] = 1;
        for(int i=s.size()-1; i>=0; i--)
        {
            for(int j=i+1; j<s.size(); j++)
            {
                if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2;
                else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
            }
        }
        return dp[0][s.size()-1];
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/683986.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Json数据 通用提取工具 Web版

Json数据 通用提取工具 Web版

问题来源 楼主使用Golang 实现了一款通用型 JSON 数据提取工具&#xff0c;支持自动识别 JSON 数据节点并有序提取为 CSV 文件。 看到大家有这样的评论&#xff0c;顺手实现下&#xff0c;~~ 尴尬的是搞完了 &#xff0c;发现 这个论坛注册不足15天&#xff0c;不能回复评论。晕…
阅读更多...
迅为RK3568开发板系统编程手册全新升级

迅为RK3568开发板系统编程手册全新升级

iTOP-3568开发板C应用编程手册全新升级&#xff0c;《iTOP-RK3568开发板系统编程手册》旨在帮助刚入门的用户进行入门规划和学习&#xff0c;为系统编程基础指导手册。 第1部分 系统编程初探 第1章 系统编程初探 1.1 什么是系统编程 1.2 系统编程的作用 1.3 系统调用和C语言库函…
阅读更多...
R语言使用xlsx包、安装包的经验以及切换工作目录的方法

R语言使用xlsx包、安装包的经验以及切换工作目录的方法

R语言使用xlsx包 首先不同于读取txt和csv文件&#xff0c;R语言读取xlsx文件需要安装xlsx包 使用下面命令进行安装xlsx install.packages(“xlsx”) 安装过程非常顺利&#xff0c;需要附带安装其它几个包。如果安装出现错误&#xff0c;可以尝试切换网络&#xff0c;使用手机热…
阅读更多...
2-css-1

2-css-1

一 CSS 初体验 CSS 定义&#xff1a;层叠样式表 (Cascading Style Sheets&#xff0c;缩写为 CSS&#xff09;&#xff0c;是一种样式表语言&#xff0c;用来描述HTML文档的呈现&#xff08;美化内容&#xff09; CSS 书写在什么位置&#xff1f; title 标签下方哪个标签里面…
阅读更多...
2-css-5

2-css-5

一 定位 1 认识 作用&#xff1a;灵活的改变盒子在网页中的位置 实现&#xff1a; 定位模式&#xff1a;position边偏移&#xff1a;设置盒子的位置 left right top bottom 2 相对定位 position: relative 特点&#xff1a; 不脱标&#xff0c;占用自己原来位置显示模式…
阅读更多...
如何将JSON对象转化为java对象，如何将java对象转化为JSON对象

如何将JSON对象转化为java对象，如何将java对象转化为JSON对象

如何将JSON对象转化为java对象&#xff0c;如何将java对象转化为JSON对象 一、在java中如何构建一个JSON对象 在java中我们可以通过创建JsonObject对象的方式来为其添加相应的参数属性&#xff0c;进而构造JSON对象 1、导入JsonObject的依赖 JsonObject是Gson库中的一个类&…
阅读更多...
数据结构--数据结构的基本概念

数据结构--数据结构的基本概念

数据结构–数据结构的基本概念 知识总览&#xff1a; 数据结构的三要素 #mermaid-svg-jflLhauniFK26Yxb {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-jflLhauniFK26Yxb .error-icon{fill:#552222;}#mermaid-svg-…
阅读更多...
软件测试已经人员饱和了？是否选择退出这个行业？

软件测试已经人员饱和了？是否选择退出这个行业？

铺天盖地的职场内卷文章充斥我们眼球&#xff0c;给大家带来山大压力&#xff0c;内心焦虑。据闻&#xff0c;2023年有1070万高校应届毕业生涌入用人市场&#xff0c;其中有多少人将卷入软件测试行业呢&#xff1f;而最近大厂毕业之风盛行&#xff0c;对外输出人才&#xff0c;…
阅读更多...
从小白到大神之路之学习运维第46天---第三阶段----Ceph分布式存储系统（CentOS7.9版本下安装部署ceph）

从小白到大神之路之学习运维第46天---第三阶段----Ceph分布式存储系统（CentOS7.9版本下安装部署ceph）

第三阶段基础 时 间&#xff1a;2023年6月25日 参加人&#xff1a;全班人员 内 容&#xff1a; Ceph分布式存储系统 目录 一、Ceph概述 二、Ceph 的工作原理和工作流程 三、Ceph 组件包括 1. RADOS 2. OSD 3. MON 4. MDS 5. RGW 6. RBD 7. CephFS 四、安装部…
阅读更多...
文心一言 VS 讯飞星火 VS chatgpt （47）-- 算法导论6.1 5题

文心一言 VS 讯飞星火 VS chatgpt （47）-- 算法导论6.1 5题

五、一个已排好序的数组是一个最小堆吗? 文心一言&#xff1a; 一个已排好序的数组不一定是一个最小堆。最小堆是一种特殊的二叉树&#xff0c;它满足以下性质&#xff1a;对于任意节点 x&#xff0c;其父节点 y 的值都小于等于 x 的值。而一个已排好序的数组只是一个有序数…
阅读更多...
【FFmpeg实战】压缩数据AVPacket解析

【FFmpeg实战】压缩数据AVPacket解析

因为FFmpeg更新的比较快&#xff0c;API也会跟着有所变动&#xff0c;所以声明一下&#xff0c;本文使用的FFmpeg版本为V3.3.5。 1.AVPacket简介 AVPacket是FFmpeg中很重要的一个数据结构&#xff0c;它保存了解复用&#xff08;demuxer)之后&#xff0c;解码&#xff08;dec…
阅读更多...
TS格式视频的使用

TS格式视频的使用

什么是TS文件格式 TS&#xff08;Transport Stream&#xff0c;传输流&#xff09;是一种封装的格式&#xff0c;它的全称为MPEG2-TS。MPEG2-TS是一种标准数据容器格式&#xff0c;传输与存储音视频、节目与系统信息协议数据&#xff0c;主要应用于数字广播系统&#xff0c;例…
阅读更多...
在加密数据时，如何选择合适的算法？

在加密数据时，如何选择合适的算法？

我们将分解两种主要类型的加密 - 对称和非对称 - 然后深入研究 5 种最常用的加密算法列表&#xff0c;以前所未有的方式简化它们 加密经常被指责为政治实体隐藏恐怖活动&#xff0c;是始终成为头条新闻的网络安全话题之一。任何对不同类型的加密有充分了解的人都可能会觉得对这…
阅读更多...
内网穿透工具cpolar——将内网站点发布至公网、远程连接公司内网电脑

内网穿透工具cpolar——将内网站点发布至公网、远程连接公司内网电脑

在现代互联的时代&#xff0c;我们经常需要将局域网中的服务器或提供给外部网络进行访问。然而&#xff0c;由于内网通常使用私有IP地址&#xff0c;在没有合适的配置和设置的情况下&#xff0c;对外部网络是不可见的。这就引出了内网穿透技术&#xff0c;它允许我们在不暴露真…
阅读更多...
从三个角度分析B端产品帮助中心的发展趋势和创新思路

从三个角度分析B端产品帮助中心的发展趋势和创新思路

随着企业级&#xff08;B端&#xff09;产品在市场上的快速增长&#xff0c;优秀的帮助中心对于提升用户体验和满意度变得尤为重要。本文将从三个维度讨论B端产品帮助中心的发展趋势和创新思路&#xff0c;以帮助企业构建更优秀的帮助体系。 个性化化的帮助体验 在B端产品帮助…
阅读更多...
基于瑞芯微camera学习原创文章汇总pdf分享给大家

基于瑞芯微camera学习原创文章汇总pdf分享给大家

前面一段时间基于瑞芯微3568平台编写了camera系列文章&#xff0c; 一共12篇&#xff0c;目前更新完毕。 《瑞芯微文章合集》 camera系列文章编写前后一共花费2个月时间&#xff0c; 期间查阅了很多资料&#xff0c;做了很多实验&#xff0c; 根据自己的理解&#xff0c; …
阅读更多...
实训笔记6.25

实训笔记6.25

实训笔记6.25 6.25一、座右铭二、知识回顾2.1 JavaSE2.1.1 基本语法2.1.2 数组2.1.3 JVM内存2.1.4 面向对象2.1.5 Java常用类2.1.6 Java异常机制2.1.7 Java泛型2.1.8 Java集合2.1.9 JavaIO流2.1.10 Java注解2.1.11 Java反射机制2.1.12 Java多线程2.1.13 Java网络编程 三、Java多…
阅读更多...
利用SpringBoot和javafx进行桌面开发

利用SpringBoot和javafx进行桌面开发

原文合集地址如下&#xff0c;有需要的朋友可以关注 本文地址 合集地址 众所周知&#xff0c;SpringBoot是一款强大的Javaweb开发程序&#xff0c;这得益于其构造了一个Spring容器&#xff0c;然后通过依赖注入和控制反转&#xff0c;维护起一套Java对象和实例的管理机制&…
阅读更多...
Chatgpt三大新功能曝光：记住你是谁/文件上传/切换工作区

Chatgpt三大新功能曝光：记住你是谁/文件上传/切换工作区

今日&#xff0c;一张神秘的截图&#xff0c;曝光了chatgpt还没发布的三个新功能&#xff1a; 除截图外&#xff0c;其对应的源代码也被扒了出来&#xff0c;甚至还有人为此建立了GitHub仓库&#xff0c;以此来追踪代码的变化情况。 根据观察&#xff0c;相关部分代码正在更新…
阅读更多...
制作看大片一样的推拉镜头效果，刚一个月AI绘图神器 Midjourney 又又更新了

制作看大片一样的推拉镜头效果，刚一个月AI绘图神器 Midjourney 又又更新了

5.1 版本刚更新一个月&#xff0c;官方又宣布 5.2 版本更新了&#xff1a;改进的美观性、连贯性、更好的文本理解、更清晰的图像、更高的变化模式、缩小绘画&#xff0c;以及用于分析提示符号的新命令 /short 命令‍‍‍‍‍‍‍‍‍ 视觉效果最神奇的功能要数 “Zoom Out” 缩…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023