目录
对于这三类问题的去重我总结的模板,直接用:
组合:
子集:
排列:
总结:
三类回溯问题框架都是
if ...终止
for 遍历
递归三类问题都抽象成树 dfs
- 对于组合和子集问题,需要用到index
- 对于排列问题不用index,但是要用used数组,来标记已经选择的元素,可以放全局,也能以引用放到参数里
- 为啥?因为排列不用index,就是每次从0开始遍历,used就是记录当前选择的这个值,然后递归进去之后还是从0开始遍历,是一定会再次碰到已选择的这个数的,used就是判断如果这个数已选择了,就continue
- 三类问题,子集问题好比取所有结点,所以if里面不用return,因为还要向下继续去取,,组合和排列if说明取到符合条件的了,那就return,返回上层,再找别的
- 对于三类问题的去重问题,注意 要去重,一定要把数据数组排序
去重的话,其实都是树层上需要去重,举个例子 1 2 1 , 目标和是3,,排序 1 1 2 ,比如求组合选定了第一个1 ,递归进去,再选择就是树枝上,就是往下延伸,懂吗。然后就得到 1 2,拿到结果了 ,递归返回去,到了for取第一个1这块,ok完了for遍历下一个,又是1 那肯定这个1就不能取了,,如果取的话又是 会取到第二个1 和2组成的一组结果,,但是这个其实是重复的
- 其实发现了没,这个树层抽象的就是for循环这个 当前循环里面++所变化, for循环遍历 0 1 2 3,这就是同一层
- 树枝向下就是进到递归
对于这三类问题的去重我总结的模板,直接用:
组合的:

组合去重:
用used数组初始化false,记录当前层这个值用过没
used数组最好别用bool,用int好点,我后面出文章说为啥少用vector<bool>

我推荐的写法: 不用used了
for里面加
// 要对同一树层使用过的元素进行跳过
if (i > index&& nums[i] == nums[i - 1]) {
continue;
}也能用set去重
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
for i=index
if (uset.count(nums[i])) {
continue;
uset.insert(candidates[i]); // 记录元素
递归
注意递归完了set不用erase,,因为set是记录每层,每层都会创建一个的子集:
if..
不return
for i=index...
递归 子集要去重的:
和组合没啥区别,组合的去重方法根子集的是一样的,三种都可以
而且他俩都用index, 唯一的区别就是if 有没有return的问题
所以子集我还是推荐这种去重写法:
for里面加
// 要对同一树层使用过的元素进行跳过
if (i > index&& nums[i] == nums[i - 1]) {
continue;
}排列:
不用index了,但是额外加个used判定数组,used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次。其实就是前面两类用来去重的used数组,只不过对于排列他,哪怕不去重也得用

排列去重:
用他本身的used数组

或者用set去重:
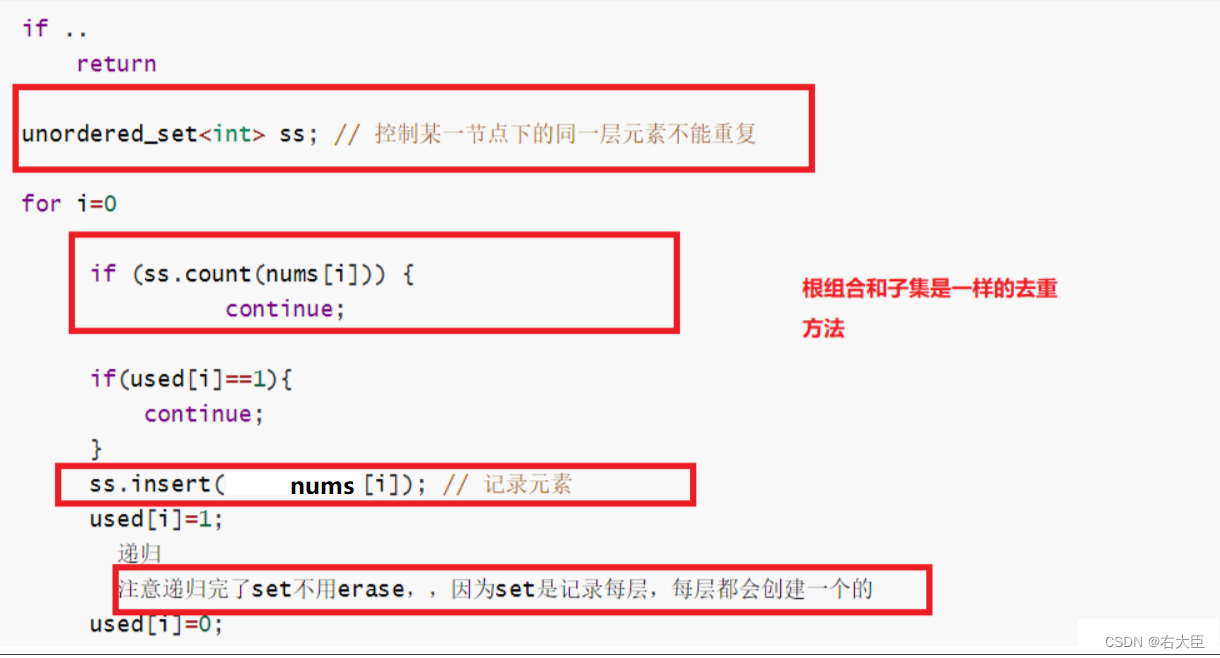
总结:
组合和子集,三种不同的去重方式,个人推荐,这种,代码少
if(i>startindex&&nums[i]==nums[i-1])
{
continue;
}排列,两种去重,哪个都行
其实看完会发现,就他们的去重方式都是一模一样的,理解抽象什么时候去重同一层数据,三种方式,自然而然就写出来了