计算物理专题：薛定谔方程的有限元解法

简单边值问题的有限元解法

$\left\{\begin{matrix} -(py')'+qy=f(x)&(a<x<b)\\ y(a)=d_1,y(b)=d_2&\end{matrix}\right.(1)$

其中： $p(x),q(x),f(x)$ 都是 $\begin{bmatrix} a,b \end{bmatrix}$ 上已知的连续函数，且 $p'(x)$ 也连续， $p(x)> 0;q(x)\ge 0$

等价性定理

如果y(x)是边值问题(1)的解，则y(x)是\mu 中使得泛函I(z)取极小值的函数；反正，如果y(x)是\mu 中使得泛函I(z)取极小值的函数，则y(x)一定是边值问题(1)的解。

$\left\{\begin{matrix} I(z)=\int_a^b\begin{bmatrix} pz'^2+qz^2-2fz \end{bmatrix}dx&(2)\\ I(y) = \min_{z\in \mu}I(z) &(3) \end{matrix}\right.$

一个常用的线性插值公式

$\begin{matrix} y(x)\approx \lambda_1(x)y_{i-1}+\lambda_2(x)y_{i}\\ \lambda_1=\frac{x_i-x}{x_i-x_{i-1}}\\ \lambda_2=\frac{x-x_{i-1}}{x_i-x_{i-1}} \\ (4) \end{matrix}$

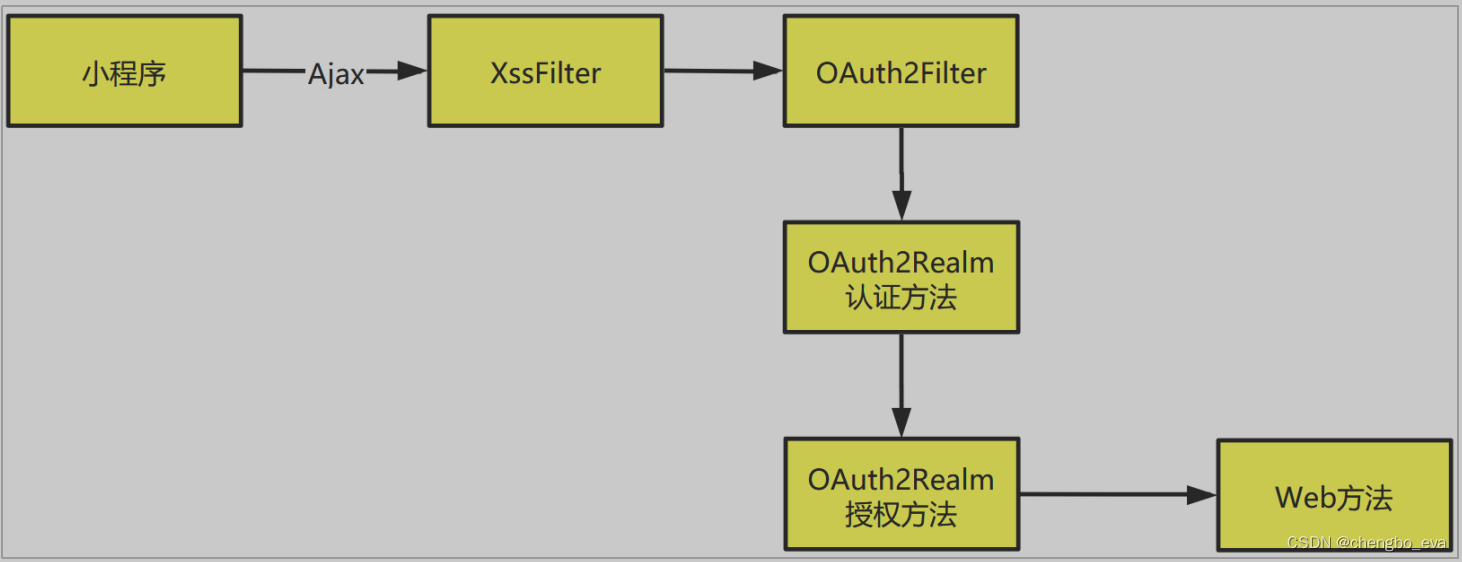
有限元法

step one

等价性定理说明，边值问题可以转换为一个变分问题。我们需要求解的是这个变分问题的数值解，反而得到边值问题的数值解。

将求解区间[a,b]剖分为n个小区间。a=x_0,x_1,x_2,...x_{n-1},x_n=b

(2) = \sum_{i=1}^n I_i;I_i = \int_{x_{i-1}}^{x_i} [[py'^2 + qy^2 - 2fy] dx

利用(4)，注意到在一系列推导后有：

$I_i \approx (y_{i-1},y_i) \begin{pmatrix} K_{11}^{(i)} &K_{12}^{(i)} \\ K_{21}^{(i)} & K_{22}^{(i)} \end{pmatrix}\begin{pmatrix} y_{i-1}\\ y_i \end{pmatrix}-2\begin{pmatrix} b_1^{(i)} &b_2^{(i)} \end{pmatrix}\begin{pmatrix} y_{i-1}\\ y_i \end{pmatrix}$

$\begin{pmatrix} K_{11}^{(i)} &K_{12}^{(i)} \\ K_{21}^{(i)} & K_{22}^{(i)} \end{pmatrix}=K^{(i)}=\frac{p_i}{l_i}\begin{pmatrix} 1 & -1\\ -1& 1 \end{pmatrix}+\frac{l_iq_i}{6}\begin{pmatrix} 2 &1 \\ 1&2 \end{pmatrix}$

$b^{(i)}=\frac{l_if_i}{2}\begin{pmatrix} 1\\ 1 \end{pmatrix}$

step two

令：

$y=(y_0,y_1,...y_n)^T;C^{(i)}=\begin{pmatrix} 0 & \dots &1 & 0& \dots & 0\\ 0 &\dots &0 &1 & \dots &0 \end{pmatrix}$

其中：

$\begin{pmatrix} y_{i-1}\\ y_i \end{pmatrix}=C^{(i)}y$

类似的，我们使：

$K=\sum_{i=1}^n C^{(i)}K^{(i)}C^{(i)};b=\sum_{i=1}^nb^{(i)}$

则可以得到

$I(y)=y^TKy-2b^Ty$

step three

由极值原理，得 $\frac{d}{dy_i}(y^TKy-2b^Ty)=0$ .

化简后可得： $\left\{\begin{matrix} \sum_{r=0}^n K_{ir}y_r = b_i(i=0,1,...,n)\\ Ky=b \end{matrix}\right.$

程序实现

import numpy as np
import matplotlib.pyplot as plt

#finite element method
def FEM(p,q,f,x0,x1,y0,y1,n=1000):
    n *= (x1-x0)
    x = np.linspace(x0,x1,n+1)
    h = (x1-x0)/n

    K = np.zeros((n+1,n+1))
    b = np.zeros(n+1)
    for i in range(1,n+1):
        xi = x[i]
        pi = p(xi)
        qi = q(xi)
        fi = f(xi)

        Ki = (pi/h) * np.array([[1,-1],[-1,1]]) + (qi*h/6) * np.array([[2,1],[1,2]])
        bi = (h*fi/2) * np.array([1,1])

        K[i-1:i+1,i-1:i+1] += Ki
        b[i-1:i+1] += bi

    K[0,0] = 1
    K[n,n] = 1
    b[0] = y0
    b[n] = y1

    y = np.linalg.solve(K,b)
    return x,y

x0 = 0
x1 = 1
y0 = 0
y1 = 0

def p(x):
    return 1

def q(x):
    return x**2

def f(x):
    return np.sin(x)*x**2

x,y = FEM(p,q,f,x0,x1,y0,y1)
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Result : FEM ')
plt.pause(0.01)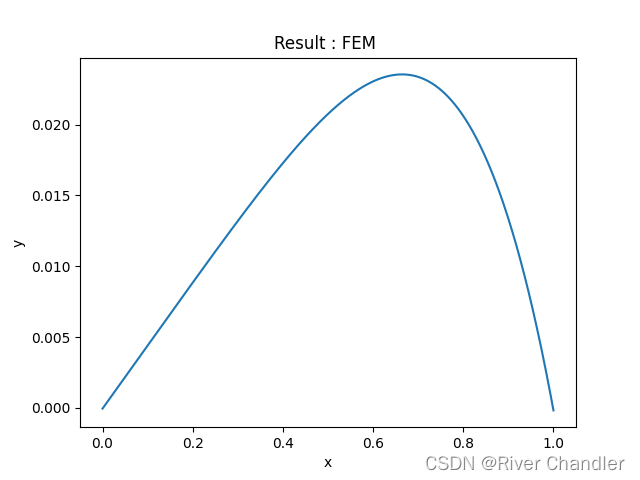

特征值问题的求解思路

一路算下去就好，寻找在端点处符合要求的值即可。

大气通讯中应用自适应光学的基本原理

自适应光学大气光学通信系统产生的激光束经过发射端的光学系统准直后平行射出。光束的波前受到大气湍流的影响发生畸变。由于像差的存在，接收端接收到的光信号无法耦合进单模光纤。波前控制器通过Zernike多项式拟合波前畸变，指导波前校正器变形。下图是激光通信自适应校正原理图：

自适应光学理论的核心是相位共轭原理。平面光波在通过湍流等折射率大于1的介质中，波前畸变可表示为：

其中A为光场振幅，是光场相位也是波前探测器采集到的信息，经过波前控制器传递给变形镜与畸变相位共轭的光场可以表示为：

通过叠加两个光场，畸变的波前将恢复平面波的状态，从而实现自适应校正像差。

湍流下的波前表示

大气湍流将导致光束在传输过程中产生波前畸变，它的Zernike多项式表达式为

Zernike多项式第一项为相位平移，对整个光束来说是相位的固定延迟或者超前。第二项，第三项式倾斜，占湍流方差的86.9%。可以用跟踪系统消除。第四到六项是离焦和像散，占湍流方差的6.7%。第四项以上的Zernike像差需要用自适应系统来校正。

而Zernike多项式系数的求解是波前模拟的目标。工程上认为是均值为0的高斯随机变量。通过校正前几项Zernike模式数达到所需的耦合效率，最终满足通信链路的性能要求。

湍流对单模光纤耦合效率的影响

光束扩展和波前畸变会导致能量弥散最终导致激光通信耦合效率的降低。对于单模光纤，自由空间传输来的激光与光纤耦合的流程图往往如下：

在大气激光通信系统中，信号光首先由大气信道输送到接收端进行探测，并经过光学透镜聚焦，与放置在焦点处的单模光纤耦合进行光电转换进而完成通信。假如大气中不存在湍流，到达光纤接收端面的信号光将形成艾里斑，则可以探测到整个接收靶面上的能量峰值，耦合效率也达到最大

在大气湍流的影响下，光波相位发生一系列的畸变最终破坏成像。

未加载自适应光学系统时的耦合效率

耦合透镜到单模光纤的距离为透镜的焦距。耦合透镜前接收到的信号光光强分布可以表示为

其中x,y是垂直于光传播方向的平面上的坐标,是湍流引入的波前相位，是孔径函数，代表光场强度。

单模光纤反向传输到镜头所在平面上的模场又可表示为：

其中为镜头平面上的光纤模场半径，是光纤接收平面上的光纤模场半径。耦合效率是指进入单模光纤的平均功率与镜头平面接收到的平均功率的比值，可以表示为，这里

由于湍流的存在，波前相位畸变导致入射光束和单模光纤的模场匹配程度下降。在这种情况下，光束经过大气湍流和自适应系统之后，和单模光纤耦合的平均功率可以表示为，其中表示波前像差的均方根，D表示接收孔的半径。

自适应光学系统对修正激光通信耦合的作用

我们用表征自适应光学系统的闭环带宽，表示大气湍流随时间变化的频率。自适应光学系统的闭环传递函数可以表示为

通过Zernike多项式拟合后得到的波前残差，可以在通信系统性能与自适应光学系统参数之间建立联系，得到平均耦合效率的公式

经过数值模拟，可以观察到校正的泽尼克模式数越多，耦合效率就越高。在弱湍流下，仅仅校正前两项即可使耦合效率达到0.4。在较强的湍流影响下，校正前50项泽尼克系数之后耦合效率能够接近0.2511。

在工程应用中，首先需要确定的是耦合效率这一指标，随后根据数值模拟的结果即可确定所需校正的最少Zernike模式数。这一模式数与哈特曼测波器的子孔径数，变形镜元数等有关。因此，在设计中，可以根据此反推出光学系统的子孔径数

大气通讯中应用自适应光学

LCRD项目

LCRD 项目实现了两台地面站(OGS1和OGS2)通过同步轨道卫星(STPSat-6)进行的激光通信中继传输。OGS1为OCTL（美国光通信望远镜实验室），OGS2 为位于夏威夷的0.6m口径望远镜。该项目也可实现国际空间站通过同步轨道卫星与地面站之间的通信。

LCRD项目在OCTL中建成了一套集成光学系统以满足观测需要。下表是IOS系统的设计指标

信标发散角	280 μrad
信号发散角	20 μrad
工作俯仰角	20°
单模光纤耦合效率	55%

图24.IOS 光机布局

LCRD采用的自适应光学系统的波前探测采用 Shack-Hartmann 传感器，波前探测相机选用的是比利时 Xenics 生产的高速 InGaAs 相机，每个子孔径照亮像元为 2×2，帧频为 10 kHz。变形镜包括低阶变形镜 LODM（Low Order Deformable Mirror）和高阶变形镜 HODM（High Order Deformable Mirror），分别用于校正低空间频率大幅度像差和高空间频率小幅度像差。InGaAs设计主镜直径上分布 28 个促动器，选用的是美国 Boston 公司 32×32 MEMS DM，行程 1.5 μm，直径约为1 cm，LODM 为 12×12 MEMS DM，行程为 3.5 μm。

大气激光通信对程序处理时长有很高的要求，处理时间越长，丢失的信息越多。数据通过DMA在帧捕获器、DSP卡和有源镜像元件之间交换，而不经过CPU，这会增加定时抖动并增加控制环路延迟，导致性能下降。

图像从帧抓取器中被逐行读出。当有两行数据可用时，它被运送到DSP板。板上的八个DSP芯片中的每一个都包含八个内核。64个内核中的每一个都测量所有小透镜的质心，但每个内核都分配了特定的DM执行器来计算命令。当计算命令时，每个DSP芯片上的DMA控制器通过DMA将DM命令传输到适当的DM。上述所有步骤都是通过DMA完成的，DMA绕过了中央处理单元（CPU），消除了CPU定时抖动。这使得对56x64像素帧的图像处理速率超过20kHz并将处理延迟保持在一位数微秒范围内。

MéO 望远镜

MéO 望远镜利用安装于 SOCRATES 微小卫星的 SOTA 终端进行了 AO 校正实验。

法国格拉斯的 MéO望远镜位于海拔1270m处，接收直径为1.5 m，指向精度小于2″，指向重复精0.1″，最大速度 5°/s。该系统采用 Shack-Hartmann 波前传感器，子孔径为 8×8，波前传感相机采用的是 First Light Imaging 公司生产的 OCAM2 相机，分辨率为 240×240。变形镜采用的是 CILAS 公司的 88 单元变形镜，stroke 大小为±5 μm，带宽达到 10 kHz。

MeO望远系统包括两个 Tip-Tilt 反射镜，一个为了光瞳稳定，带宽为10 Hz，一个为了校正大气湍流引起的倾斜，带宽为 2 kHz。校正后光斑图像可通过像素大小为 6.5 μm 的 sCMOS 相机记录。