在关系R<U,F>中,U=ABCDEG
F={BG->C,BD->E,DG->C,ADG->BC,AG->B,B->D}
先进行第一大步:
先看右边:
如果有BG->C,G-->C,因为单G就可以推出C了就不需要BG--->C了,可以把BG--->C这个冗余的去掉,根据F中的关系,没有此项,就可以跳过此步。
再看中间:
第一个:BG--->C以外的推导式能否推出BG--->C
G=F-(BG-->C)=BC-->E,DG---->C,ADG-->C,AG-->B,B--->D
注:若BG为x0,则x1表示能从BG推出来的字母...
x0=BG(G+) x1=BG+D=BGD x2=BGD+EC=BCDEG x3=BCDEG 推不出新字母了,停止
我们发现BCDEG中包含C,所以BG---->C冗余
第二个:BD-->E同理
G=F-(BD-->E)=DG-->C,ADG-->C,AG--->B,B--->D
x0=BD(G+) x1=BD+D=BD 停止
BD中不包含E,不能将此推导式删除
第三个:DG-->C
F=BD→E,DG→C,ADG→C,AG→B,B→D
G=F-(DG→C)=BD→E,ADG-->C,AG→B,B→D
x0=DG(G+) x1=DG+NULL=x0 停止
DG中不包含C,不能将此推导式删除
以此类推得到以下推导式不能删除:
F=BD→E,DG→C,AG→B,B→D
所以F={BD→E,DG→C,AG→B,B→D}
现在进行第二大步:
再进行逐个细化:
BD--->E
先划掉B,则x0=D x1=D
再划掉D,则x0=B,x1=BD,x2=BDE,发现包含E,所以删除B-->E
所以F={D--->E,DG--->C,AG-->B,B--->D}
DG-->C同理
先划去D,x0=G,x1=G
再划掉G x0=D,x1=D
以此类推得到F={D--->E,DG--->C,AG-->B,B--->D}
重复以上第一大步和第二大步,直到无法删除任意一个字母
所以候选码,根据这个F找(重点)
1.如果这个属性只在左端出现了,那么必定是候选码(即候选码至少要包含A,G)
2.如果这个属性只在右端出现了,那么必定不是候选码
3.如果属性在两端出现了,那么是后备(如果主属性A,G足以推出全局,那么候选键就是A,G,如果不能,那么就在后备中找,一个一个试,看能否推出全集)
4.还有两端都不在的字母
具体做法如下
设定左端为L,右端为R,既在左端又在右端为LR,两端都不在N
令X=L N,求X的闭包
1.如果包含了R的所有属性,那么X为R的唯一候选键。
2.如果没有包含,那么从后备,即两端都有的字母中加入候选键一个一个试
接上面的例子:F={D--->E,DG--->C,AG-->B,B--->D}
x0=L N=AG x1=AG+B=AGB x2=AGB+D=ABGD x3=ABGD+EC=ABCDEG=U
AG(F+)=U:AG在F上的闭包=全集U,所以AG是候选码
再来几个例题:
例1:
设关系模式R(ABCD)
F={AB-->C,C-->A,C--->D}
L=B,R=D,LR=A,C,N=空集
x0=L N=B x1=B,不等于U
先选择A
x0=AB x1=ABCD,等于U
再选择C
x0=BC x1=ABCD,等于U
所以候选键是AB,AC
例2:
F={A-->BC,C-->AD}
L=空集,R={B,D} LR={A,C}
x0=A x1=ABCD ,等于U
x0=C x1=ABCD,等于U
所以候选键是A,C
例3:
关系模式R{A,B,C,D,E,F,G},函数依赖F={A--->BC,BC--->A,BCD--->EF,E---->C},求R的候选键
L={D} R={F} LR={A,B,C,E} N={G}
x0=DG x1=DG,不等于U
先从LR中选择一个字母:
A x0=ADG x1=ADGBCEF=U 所以候选键可以是ADG
B x0=BDG x1=BDG,不等于U
C x0=CDG x1=CDG,不等于U
E x0=EDG x1=EDGC,不等于U
注意A一定要划去,现在选2个
BC x0=BCDG x1=BCDGAE=U 所以BCDG是候选键
BE x0=BEDG x1=BEDGCAF=U 所以BEDG是候选键
CE x0=CEDG x1=CEDG,不等于U
所以候选键是ADG,BCDG,BEDG
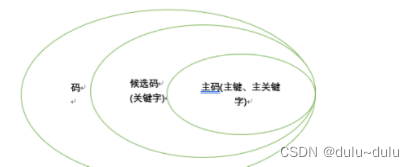
补充:这里一定要区分主属性和候选码:
1.候选码的定义:如果关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码;
2.主码的定义:如果一个关系有多个候选码,则选定其中一个为主码;
3.主属性定义:候选码的主属性称为主属性;
4.非主属性定义:不包含在任何候选码中的属性称为非主属性;
补充:将这个属性集的依赖关系规范为三范式:
对于范式我这里不细讲,如果不清楚可以看:http://t.csdn.cn/79MwB
U1=AGB(F=AG--->B)
U2=BDE(F=BD-->E,B-->D)
U3=CDG(F=DG---C)
分解成这样,才能既没有部分依赖也没有传递依赖。