题目

在 LeetCode 商店中，有n件在售的物品。每件物品都有对应的价格。然而，也有一些大礼包，每个大礼包以优惠的价格捆绑销售一组物品。
给你一个整数数组price表示物品价格，其中price[i]是第i件物品的价格。另有一个整数数组needs表示购物清单，其中needs[i]是需要购买第i件物品的数量。还有一个数组special表示大礼包，special[i]的长度为n + 1，其中special[i][j]表示第i个大礼包中内含第j件物品的数量，且special[i][n]（也就是数组中的最后一个整数）为第i个大礼包的价格。
返回确切满足购物清单所需花费的最低价格，你可以充分利用大礼包的优惠活动。你不能购买超出购物清单指定数量的物品，即使那样会降低整体价格。任意大礼包可无限次购买。

示例

输入：price = [2,5], special = [[3,0,5],[1,2,10]], needs = [3,2]
输出：14
解释：有 A 和 B 两种物品，价格分别为 ¥2 和 ¥5 。大礼包 1 ，你可以以 ¥5 的价格购买 3A 和 0B 。大礼包 2 ，你可以以 ¥10 的价格购买 1A 和 2B 。需要购买 3 个 A 和 2 个 B ，所以付 ¥10 购买 1A 和 2B（大礼包 2），以及 ¥4 购买 2A 。

题解

该问题就跟平时我们去商场购物一样，大礼包就是多种商品凑一起的打折方式。这里以上题示例来进行说明，price=[2,5]表示有两个商品A与B
其中A商品的单价是2，B商品的单价是5。special就是所谓的大礼包，special = [[3,0,5],[1,2,10]]，表示其一共有两个大礼包或是打折方式，一种是[3,0,5]表示A商品3个B商品0个的打折价是5，这明显比直接买3个A商品6的价格要便宜。[1,2,10]表示买1个A商品2个B商品的打折价是10显然要比单独买1个A商品2个B商品要便宜。needs=[3,2]中需要购买的商品数，其中需要A商品3个B商品5个。这里的问题是购买购物清单里的商品最少花费多少。这里有一个限制是所有商品的数量不能超过购物清单的数量，即使打折的价位很便宜。

思考过程

我比较喜欢通过人为的判断过程来整理思路。因为题目给出的special并一定都比单独买便宜，因为需要确定有效的special。示例中的两个special显然要比单独买便宜，因此均有效。

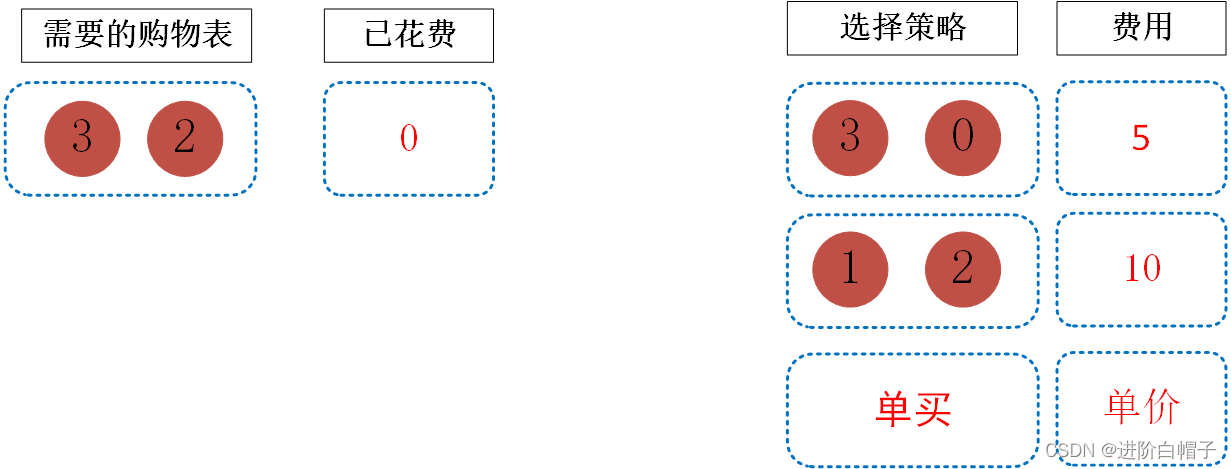
在这里插入图片描述

如上图所示为初始状态，需要的购物表为needs列表。其中的选择策略要么是大礼包，要么是单买。那么接下来我们如何选择呢，如果大礼包有效的话，那么肯定首选大礼包。
在这里插入图片描述

大礼包1明显满足要求，在选择大礼包1后，购物列表减少变为[0,2]，当前花费了大礼包1的价格5。我们也发现其实也可以选择大礼包2。
在这里插入图片描述

选择大礼包2的情况如上图所示。但是到这里我们没办法判断是选择大礼包1好些还是选择大礼包2好些。这里还有一个单买为什么不一起考虑，之前讨论过，有效的大礼包是肯定要比单买便宜的，因此有大礼包可选择就不需要考虑单买。

在这里插入图片描述

继续分别考虑，由于需要购物的列没有满足要求的大礼包因此只能单买，这两种情况的价位分别是15与14。到此，其实思路已经很明确了。整个过程改变的量只有需要的购物表，求得的最小的花费。由于购物表的状态变化是可以自底向上的，我一开始考虑的是使用动态规划。但是在写代码的过程中发现dp中的维度是一个变量，也就是购物表中的物品是一个不确定量，这导致无法自底向上的构建状态矩阵。我个人一直认为动态规划=递归+记忆化搜索。因此，这里直接考虑使用递归+记忆化搜索。
递归的思路：

输入：需要的购物表
输出：最小花费
过程：首先是边界判断，最坏的情况就是所有物品都单买，这里作为上界。遍历每个大礼包，考虑选择该大礼包的花费

初始代码：

class Solution:
    def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:
        #过滤掉无用的大礼包
        usefull_special=[]
        for sub_spe in special:
            spe_price=sum([item[0]*item[1] for item in list(zip(sub_spe[:-1],price))])
            print(spe_price,sub_spe[-1])
            if spe_price>sub_spe[-1]:
                print(sub_spe)
                usefull_special.append(sub_spe)

        #递归函数dfs(need_list)返回need_list的最小
        def dfs(needs_list):
            # 不购买任何大礼包人情况下，所有物品单独买是购物价格的上限
            min_price = sum(need * price[i] for i, need in enumerate(needs_list))
            #终止条件所有needs_list均为0
            if all(item==0 for item in needs_list):
                return min_price
            #分情况讨论，首先是判断能使用大礼包的情况
            for special in usefull_special:
                #判断大礼包是否可使用
                curr_needs=[needs_list[i]-special[i] for i in range(len(needs_list))]
                if all(item>=0 for item in curr_needs):
                    min_price=min(min_price,special[-1]+dfs(curr_needs))
            return min_price
        return dfs(needs)

优化

可以使用装饰器 @lru_cache(None) 实现记忆化搜索，由于记忆化搜索不支持list输入，把list转换成tuple。

代码如下：

class Solution:
    def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:
        #过滤掉无用的大礼包
        usefull_special=[]
        for sub_spe in special:
            spe_price=sum([item[0]*item[1] for item in list(zip(sub_spe[:-1],price))])
            print(spe_price,sub_spe[-1])
            if spe_price>sub_spe[-1]:
                print(sub_spe)
                usefull_special.append(sub_spe)

        #递归函数dfs(need_list)返回need_list的最小
        @lru_cache(None)
        def dfs(needs_list):
            # 不购买任何大礼包人情况下，所有物品单独买是购物价格的上限
            min_price = sum(need * price[i] for i, need in enumerate(needs_list))
            #终止条件所有needs_list均为0
            #if all(item==0 for item in needs_list):
                #return min_price
            #分情况讨论，首先是判断能使用大礼包的情况
            for special in usefull_special:
                #判断大礼包是否可使用
                curr_needs=[needs_list[i]-special[i] for i in range(len(needs_list))]
                if all(item>=0 for item in curr_needs):
                    min_price=min(min_price,special[-1]+dfs(tuple(curr_needs)))
            return min_price
        return dfs(tuple(needs))

复杂度分析

时间复杂度： $O(n×k×m^n)$ ，其中 $k$ 表示大礼包的数量， $m$ 表示每种物品的需求量的可能情况数（等于最大需求量加 1）， $n$ 表示物品数量。我们最多需要处理 $m^n$ 个状态，每个状态需要遍历 $k$ 种大礼包的情况，每个大礼包需要遍历 $n$ 种商品以检查大礼包是否可以购买。
空间复杂度： $O(n×m^n)$ ，用于存储记忆化搜索中 $m^n$ 个状态，每个状态需要存储n个商品的需求。