(这里写自定义目录标题)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、树的概念?
- 二、树的表示方法
- 三、树的实际应用
- 四、二叉树概念以及结构
- 1.概念
- 2.特殊的二叉树
- 3.二叉树的性质
- 4.二叉树的存储结构
- 5.引入堆的概念以及结构
- 6.堆的实现以及堆排序
- 7.时间复杂度问题
- 8.TPopk问题
- 总结
前言
树形结构是一种非线性的数据结构,其应用非常广泛,由树形结构可以引申出二叉树、堆等等的特殊树。
学习树对我们今后的工作帮助非常大。
一、树的概念?
树是一种非线性的数据结构,它是n(n>=0)个有限结点组成的一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它根朝上,而叶朝下。简单来讲就是–>树+人类亲缘关系描述
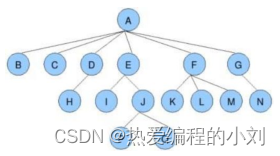
**- 根结点:没有父结点,且为所有结点的祖先的结点,如上图的A
- 节点的度:一个节点含有的子树个数称为该节点的度,如上图:A-6、D-1、E-2
- 叶子节点:度为0的结点,如上图的B、C
- 分支节点:度不为0的结点,如上图的D、E、F
- 父节点:一个节点含有子节点的节点,称为父节点,如:A为B、C、D、E的父节点
- 子节点:一个节点有父节点的节点称为子节点,如:B、C、D、E为A的子节点
- 兄弟节点:具有相同父节点的节点,如:I、J的父节点都为E,则I和J为兄弟节点
- 树的度:一棵树中,最大的节点度,如上图:树的度为6
- 节点的层次:从根节点开始算,根为1,依次往下计算
- 树的高度或深度:树的节点最大层,如上图:4
- 堂兄弟:处于同一层,但又不是兄弟节点的节点
- 节点的祖先:从根节点到所经分支上的所有节点
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙,如:所有节点都是A的子孙
- 森林:由多棵不相交的数组成**
二、树的表示方法
树的存储表示既要保存值域,也要保存节点和节点之间的关系,实际中树的表示方法有很多种,如:双亲表示法、孩子表示法等等,但我们最常用的还是孩子兄弟表示法。

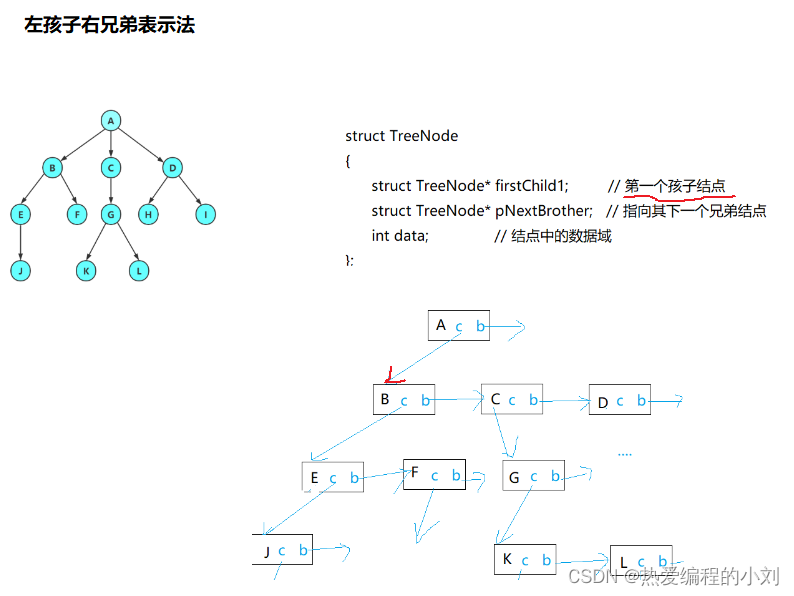
三、树的实际应用
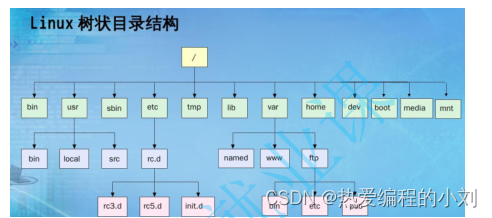
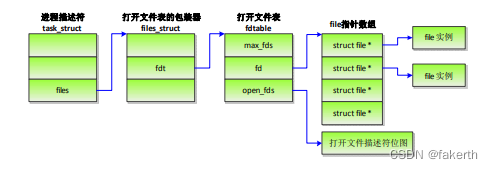
在实际应用中,树结构常常用于制作文件目录
四、二叉树概念以及结构
1.概念
一棵二叉树是结点的一个有限集合,构成二叉树有规定:
1.一定是由一个根节点加上两棵左子树和右子树组成
2.二叉树不存在大于2的节点
3.二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2.特殊的二叉树
- 满二叉树
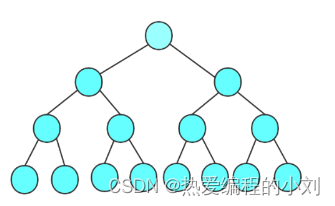
每一层的节点数都达到最大值,则称这个二叉树为满二叉树,就是说,如果一个二叉树层数为h,且节点总数为2^h-1,则为满二叉树
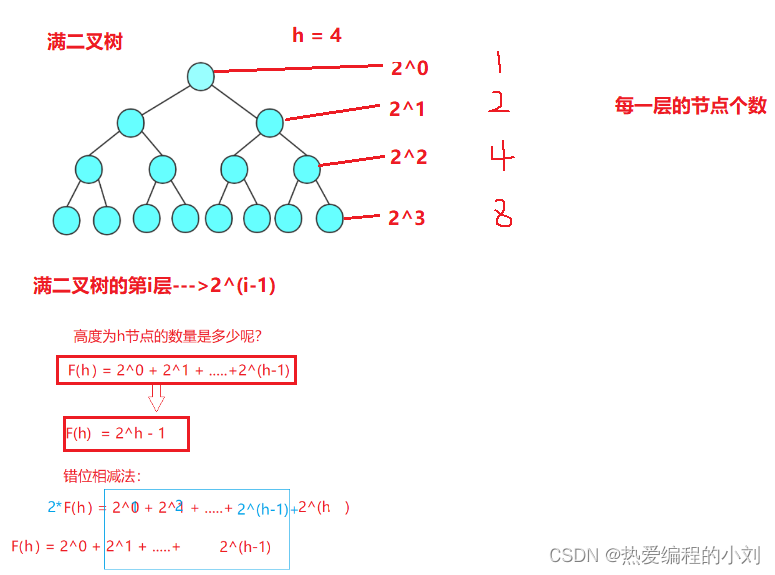
2.完全二叉树
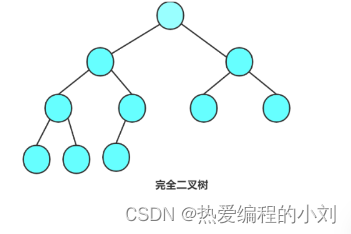
完全二叉树为(最后一层-1)层必须为满节点,最后一层可以没有分支节点,若有,则需要有序。
注意:满二叉树是一种特殊的完全二叉树
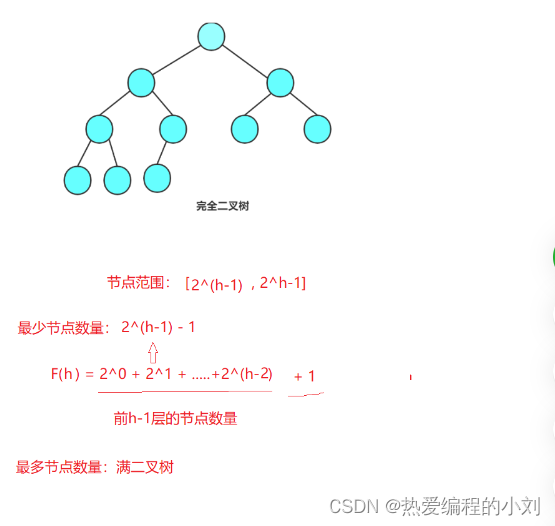
3.二叉树的性质
3.1 如何计算高度为h的节点个数?
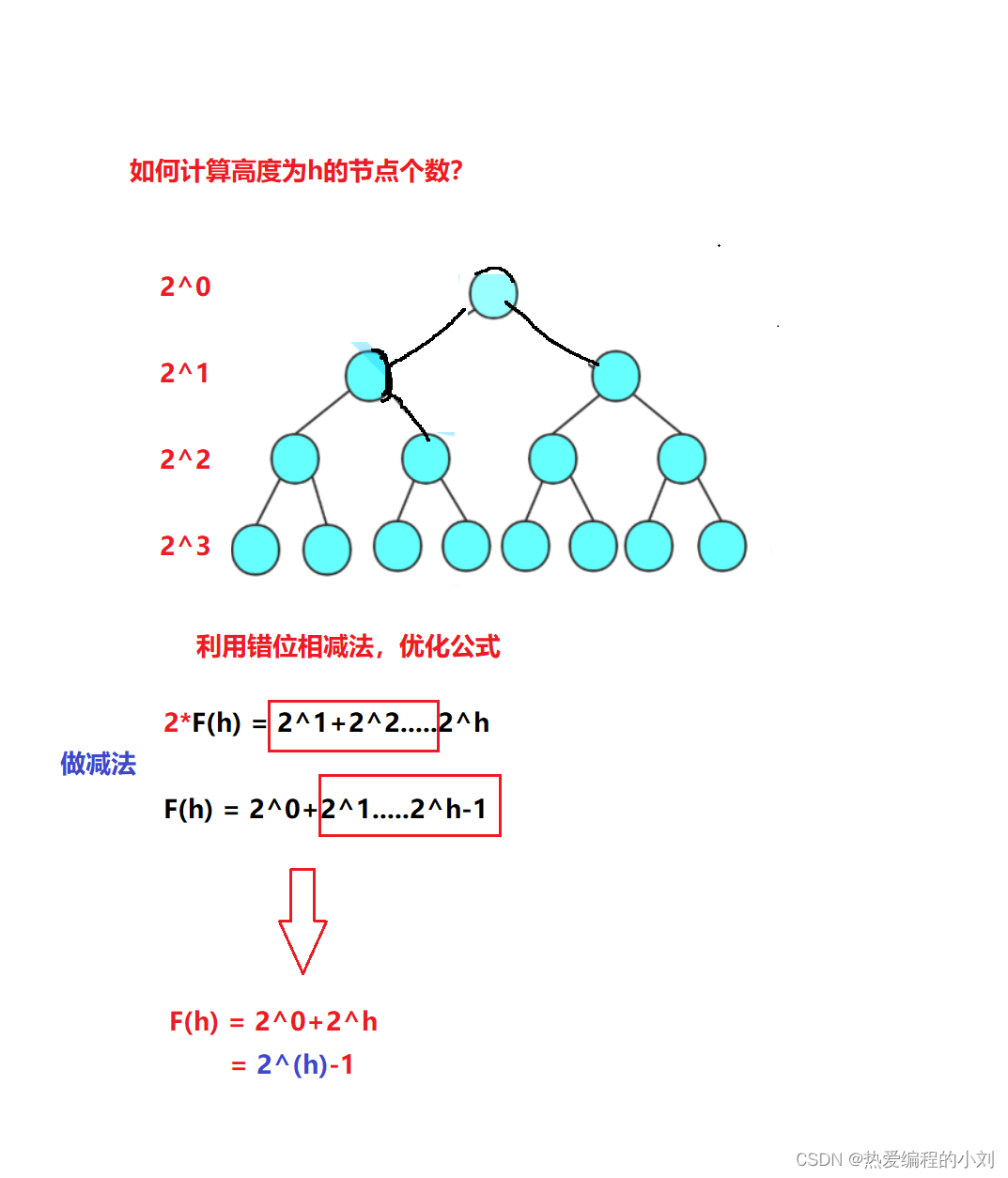
3.2 如何计算二叉树的高度(h)
已知节点个数,求高度(h)
N为节点个数
公式:(2^h)-1 = N ⇒ F(h) = log N+1;
4.二叉树的存储结构
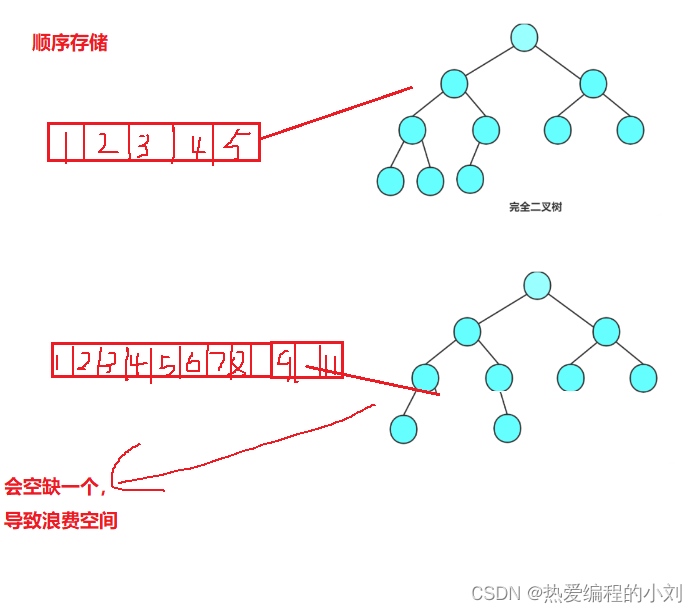
- 顺序存储
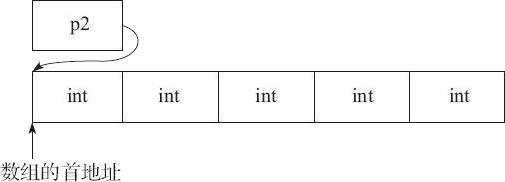
顺序结构存储就是用数组进行存储,但一般用数组进行存储只用来存储完全二叉树,因为不是完全二叉树会有空间浪费,起原因是完全二叉树的子树必须是一个接着一个的,而其它形式的没这种规定
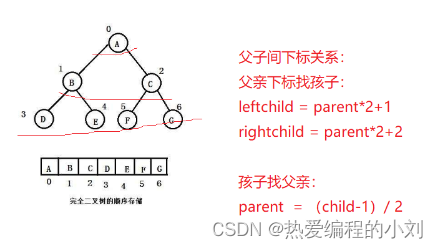
父子间下标关系:
5.引入堆的概念以及结构
1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为会浪费大量的空间,而往往在现实中,我们会把堆(一种二叉树)使用顺序结构的数组进行存储。
2.堆
2.1、是一种完全二叉树。
2.2、大堆:树中任何一个父亲都大于或等于孩子
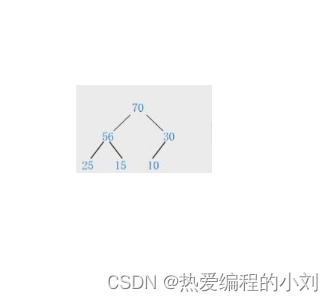
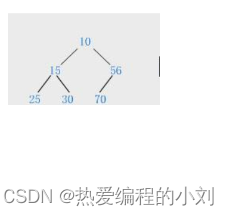
小堆:树中任何一个父亲都小于或等于孩子
6.堆的实现以及堆排序
核心算法:
6.1 向上调整算法
前提:是一个堆

6.2 向下调整算法
前提:左右子树是一个堆

7.时间复杂度问题
向上调整建堆:
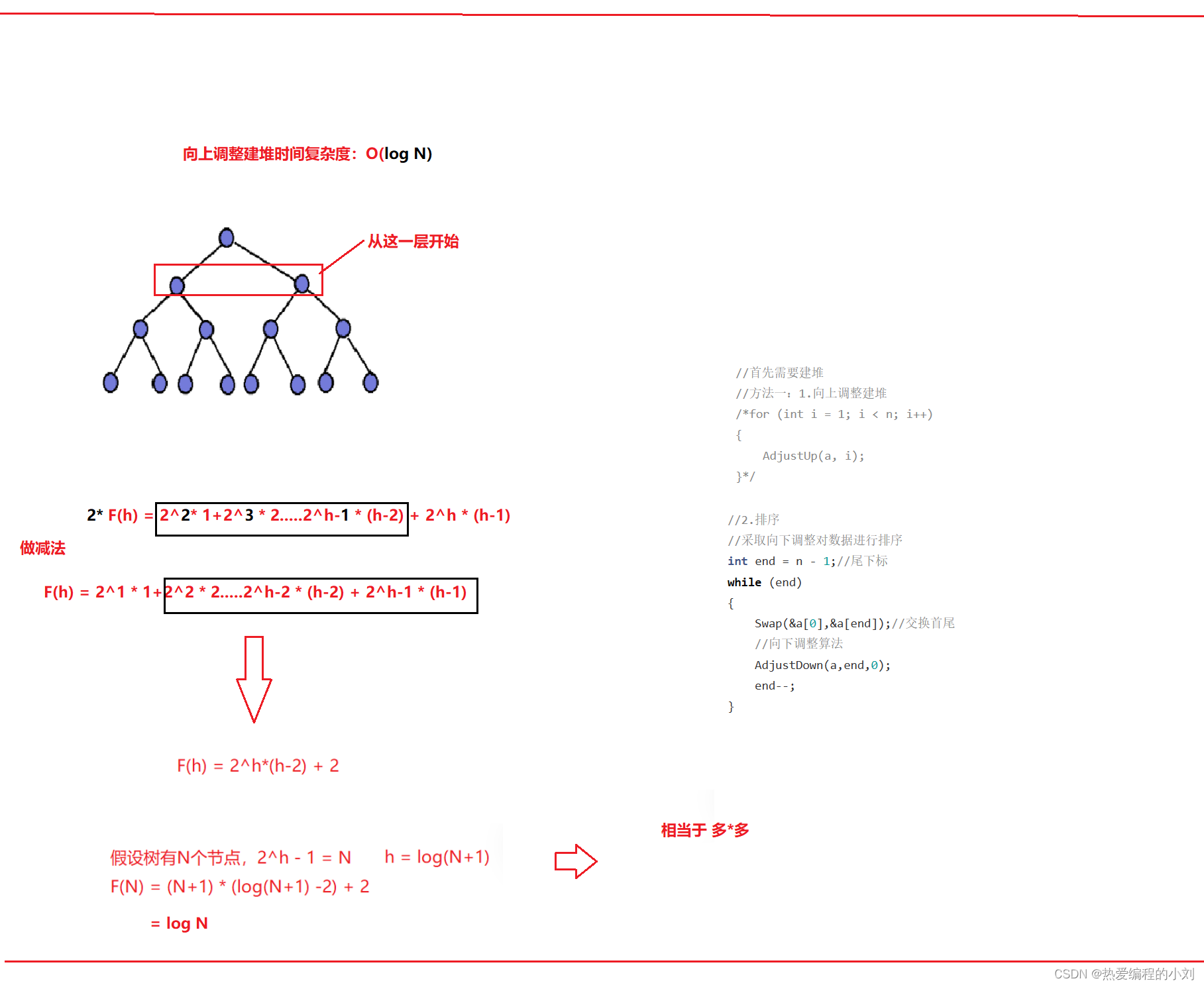
向下调整建堆
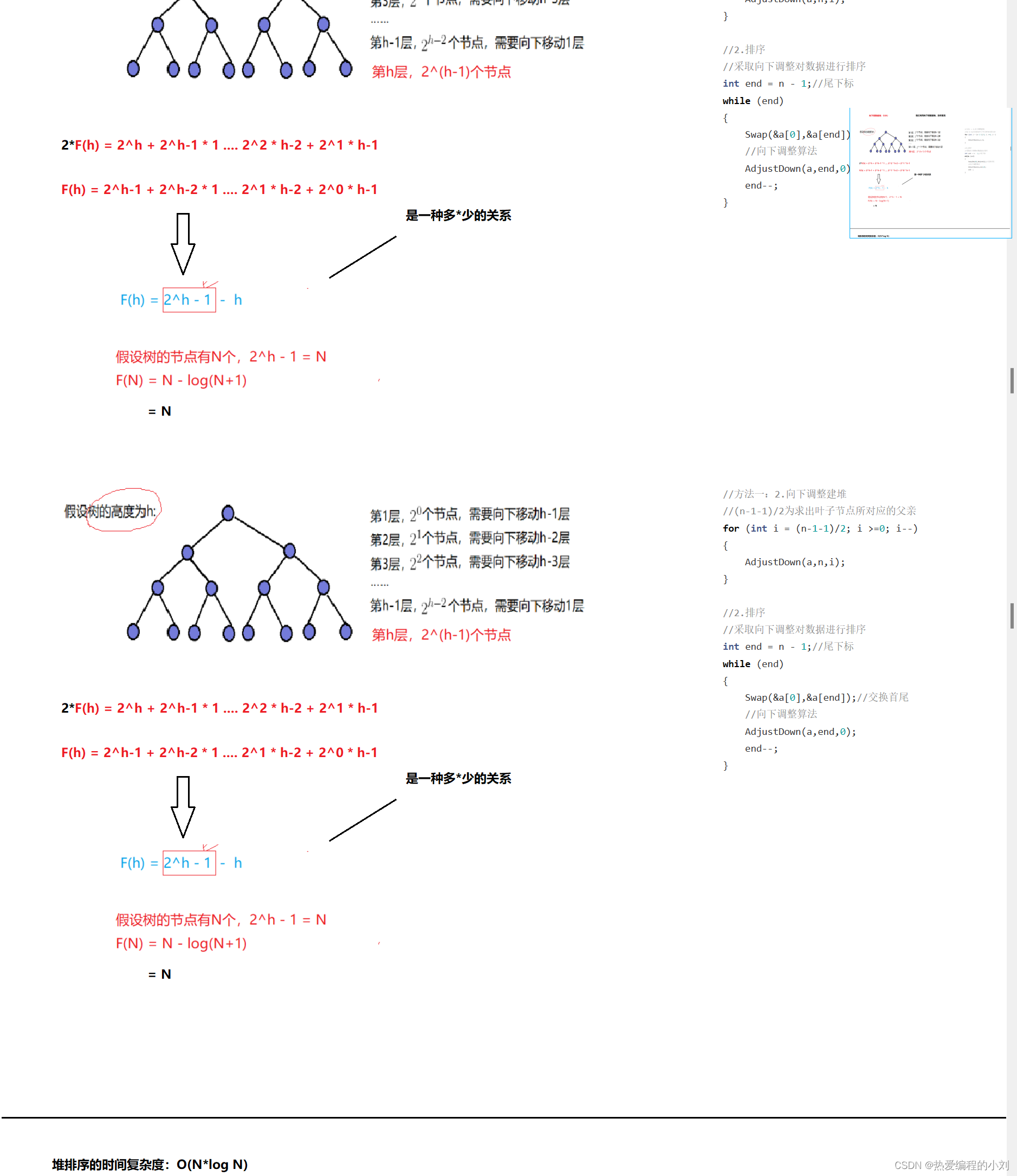
堆排序
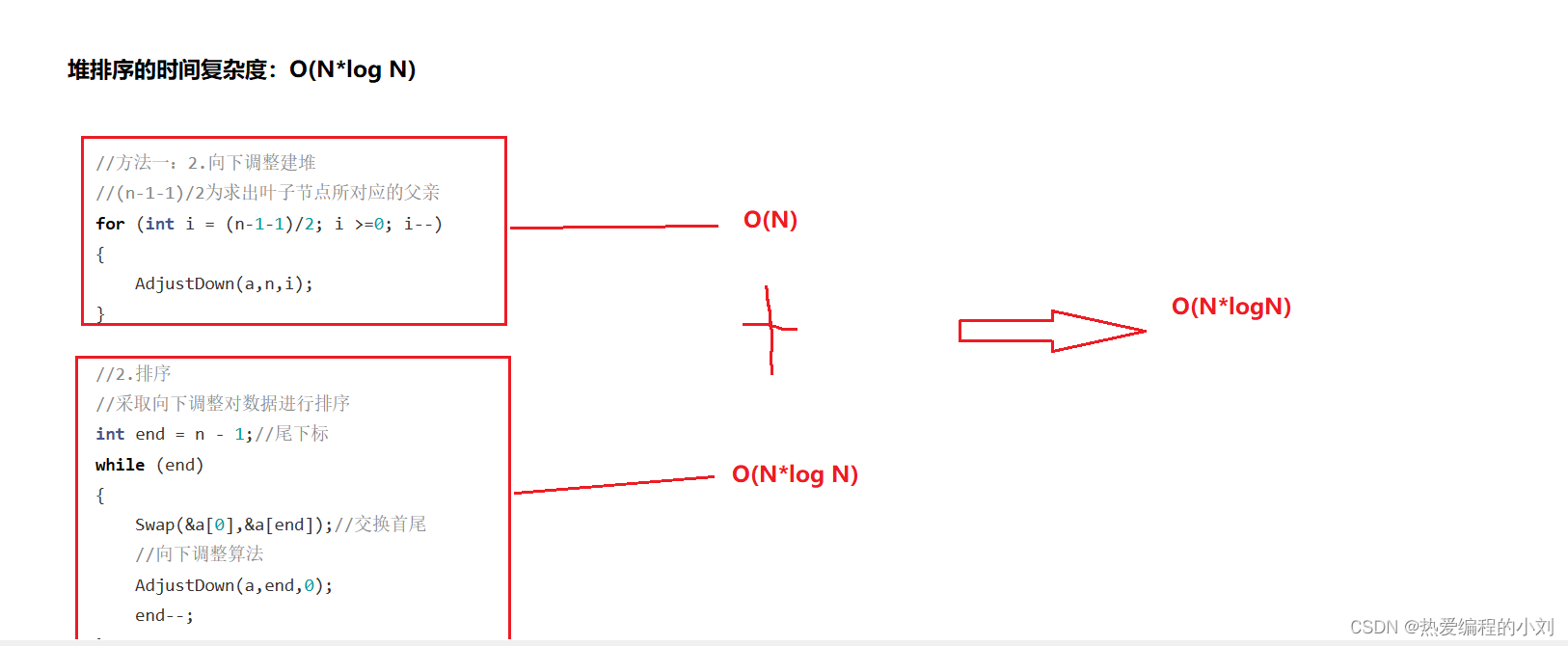
8.TPopk问题
什么是TPopk问题?
TPopk问题是堆的应用之一,其是要实现N个数中找出最大/最小数的前K个.
实现方法:
1.用于简单场景,如N的值不大的情况

//找出前k个最大的数
void Swap(int* father, int* child)
{
int tmp = *father;
*father = *child;
*child = tmp;
}
void AdjustDown(int* tpopk, int n,int father)
{
int child = (father * 2) + 1;
while (child<n)
{
if (child+1<n && tpopk[child]<tpopk[child+1])
{
child++;
}
if (tpopk[father] < tpopk[child])
{
Swap(&tpopk[father], &tpopk[child]);//交换
father = child;
child = (father * 2) + 1;
}
else
{
break;
}
}
}
void Adjustcreate(int* tpopk,int n)
{
for (int i = (n-1-1)/2; i >=0; i--)
{
AdjustDown(tpopk,n,i);
}
}
void AdjustPop(int* tpopk,int n)
{
//交换首尾元素
Swap(&(tpopk[0]), &(tpopk[n - 1]));
n--;
AdjustDown(tpopk, n, 0);
}
void TPopk(int* tpopk, int n)
{
//1.建堆
//采用向下调整建堆
Adjustcreate(tpopk,n);
//2.Tpop数据后,Pop数据
printf("%d ", tpopk[0]);
for (int i = 0; i < 4; i++)
{
AdjustPop(tpopk, n--);
printf("%d ", tpopk[0]);
}
}
int main()
{
int tpopk[] = {5,2,9,6,1,4,10,50};
int size = sizeof(tpopk) / sizeof(int);
TPopk(tpopk,size);
return 0;
}
2.用于复杂场景,如N的值太大的情况
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void Swap(int* child,int* father)
{
int tmp = *child;
*child = *father;
*father = tmp;
}
void AdjustDown(int* a,int k,int father)
{
int child = (father * 2) + 1;
while (child<k)
{
if (child+1<k && a[child] >a[child+1])
{
child++;
}
if (a[child]<a[father])
{
Swap(&a[child],&a[father]);
father = child;
child = (father * 2) + 1;
}
else
{
break;
}
}
}
void AdjustDownC(int* a,int k)
{
for (int i = (k-1-1)/2; i >=0; i--)
{
AdjustDown(a,k,i);
}
}
void PrintTopK(int* a,int n,int k)
{
//1.将前K个数建堆
AdjustDownC(a,k);
//2.将N-K的数,依次与堆顶元素比较
for (int i = k; i < n; i++)
{
if (a[0] < a[i])
{
Swap(&a[0],&a[i]);
AdjustDown(a,k,0);
}
}
}
void Topk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int) * n);
if (a == NULL)
{
perror("malloc fail:");
return;
}
srand((unsigned int)time(0));
for (int i = 0; i < n; ++i)
{
a[i] = rand() % 100;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
}
int main()
{
Topk();
return 0;
}
总结
这就是我对堆的应用与理解,谢谢观看!
![指针与数组--动态数组(2)[1、长度可变的一维动态数组 2、长度可变的二维动态数组]](https://img-blog.csdnimg.cn/7fb31292063940e4bdbe1d39a5bc8117.png)