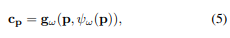0. 简介

现有的视觉SLAM很多的算法让仍然是基于特征提取的方法来完成地图的建立，而RGB-D传感器的算法仍然是主要基于稀疏点的SLAM系统，这就导致在构建稠密点云地图的时候需要保持大量的地图点来建模环境。大量的地图点给我们带来了很高的计算复杂性，使其难以部署在移动设备上。另一方面，平面是人造环境中常见的结构，特别是在室内环境中。我们通常可以使用少量的平面来表示一个大的场景。《VIP-SLAM: An Effificient Tightly-Coupled RGB-D Visual Inertial Planar SLAM》一文就解决了这一问题，通过降低基于稀疏点的SLAM的高复杂性。我们建立了一个由几个平面和地图点组成的轻量级后端建图，以实现具有相同或更好精度的高效捆集调整（BA）。在优化过程中，利用单应性约束消除了多个平面点的参数，降低了BA的复杂性。对单应性约束和点到平面约束中的参数和测量值进行分离，并对测量部分进行压缩，进一步有效地提高BA的速度。我们还将平面信息集成到整个系统中，以实现鲁棒的平面特征提取、数据关联和全局一致的平面重建。

1. 主要贡献

在本文之前，有很多融合IMU的工作表明，IMU有助于提高系统的鲁棒性，而结构化平面有助于提高系统的精度和鲁棒性。此外，与线和点特征相比，平面可以使用更少的参数来模拟环境。基于此，我们充分利用多个传感器的特点，提出了一种高度鲁棒和精确的系统，它集成了IMU，RGB，Depth和Plane信息。本文有三个贡献:

1. 我们首先提出了一个完整的紧耦合的多传感器融合SLAM系统，以融合RGB、深度、IMU和结构化平面信息。将所有信息集成到一个统一的非线性优化框架中，共同优化关键帧姿态、IMU状态、点和平面的参数；

2. 我们引入平面信息来减少地图点的数量，加快BA的优化。我们使用单应性去除优化过程中该点的状态，并将多个约束同时压缩为一个约束。这些措施减少了优化时间，图4(a)和图4(b)显示了这个过程；

3. 将平面信息集成到整个SLAM系统中，实现高精度跟踪。我们使用纯几何单帧点到平面约束来提高无纹理场景平面估计的精度和稳定性。此外，我们将平面点的重投影转换为单应性约束，以建立多帧与平面之间的关系，以进一步纠正漂移。

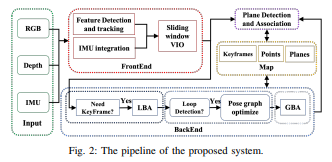
2. 系统概述

图2显示了所提出系统的概述。我们的系统以RGB，深度和IMU为输入，具有三个主要组件，包括前端，平面模块和后端。
前端模块是基于滑动窗口的VIO系统，可实时估计6-DoF姿态。我们的VIO类似于[7]，只是我们不考虑SLAM特征并添加额外的深度测量。
平面模块接收前端和后端数据作为输入。高频前端信息仅用于扩展平面。低频但高精度后端信息用于新平面检测，平面扩展，点到平面关联和平面到平面合并。由于室内环境的大多数平面是水平的或垂直的，因此我们只考虑水平和垂直平面的检测。然而，关于平面的融合优化适用于一般平面。
后端模块使用局部束调整（LBA）或全局束调整（GBA）来联合优化平面、点、IMU状态和关键帧姿态，并纠正前端姿态的漂移。

3. 文章中各种符号标记

我们首先定义本文中使用的符号。我们将$(\cdot {)}^W$视为世界坐标系。 $(\cdot {)}^C$是相机坐标系，$(\cdot {)}^I$是IMU坐标系。我们用$T\in SE(3)$表示姿态，其由旋转$R\in SO(3)$和平移$t\in R^3$组成。我们使用$\pi =[n;d{]}^T$表示平面，其中$n$是平面法线，$d$是原点与平面之间的距离。我们采用CP[28]向量来参数化平面$\pi$，即$\eta =nd$。$X$是需要估计的状态，包括姿态，速度，IMU偏差，点和平面地标。

4. 前端

当收到新图像时，我们检测ORB特征[1]点并计算相应的描述符。首先，我们使用KLT将它们从上一幅图像跟踪到当前图像。然后，我们将具有3D信息的特征投影到当前图像上，并使用汉明距离来找到最近的ORB特征点。其余的特征通过使用KLT跟踪的结果作为初始值来找到最佳观察来匹配。最后，我们使用基于RANSAC的基本矩阵来去除异常值。
运动估计是基于滑动窗口的VIO，它紧密地集成了RGB，深度和IMU。我们的VIO类似于[7]，它使用平方根逆滤波器来融合所有测量值。主要区别在于我们不考虑SLAM特征，并在视觉测量中添加深度信息。

5. 平面识别与关联

5.1 平面检测和合并

平面检测 平面模块只能使用后端数据检测平面。检测到平面后，平面模块使用前端和后端数据扩展平面并将平面与地图地标相关联。类似于[17]，我们使用Delaunay三角剖分来创建3D网格和直方图来检测平面。我们只检测垂直和水平平面，通过检查网格法向量是否垂直或平行于重力。我们的平面模块采用一些额外的方法来提高平面精度。当从直方图中检测到平面时，我们将使用数据和直方图中的3D平面点来细化其参数，而不是直接使用直方图的比例值。对于水平平面，我们只需设置$n=[0,0,1{]}^T$并将平面距离设为平面点的z轴的平均值。对于垂直平面，我们设置$n=[n_x,n_y,0{]}^T$，并使用以下方程细化垂直平面参数:

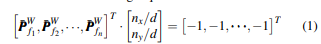
其中，$n$是平面点的数量，$P_{f_k}^W$ 是世界坐标系下第$k$个地标的位置，${\bar{P}}_{f_k}^W=[P_{f_k}^W(0),P_{f_k}^W(1){]}^T$。我们使用QR分解来解决方程(1)。当检测到平面参数时，平面可以通过角度和距离与3D网格相关联。我们的角度和距离阈值约为10度和5厘米。图3显示了这个过程。

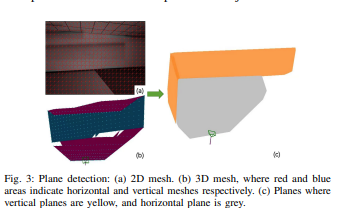
图3.平面检测：(a)2D网格。(b)3D网格，其中红色和蓝色区域分别表示水平网格和垂直网格。©垂直平面为黄色，水平平面为灰色。

5.2 点与平面关联

我们使用3D网格将更多的地图点与平面相关联。 一旦深度图中的3D网格与一个平面相关联，我们就会找到它的2D网格。如果地图点的2D坐标在2D网格内并且地图点与平面的距离小于10厘米，则将地图点添加到与平面相关联的候选集合中。如果候选集合上的点在3个关键帧以上被观察到，我们将检查其几何一致性。我们计算点的重投影误差，强制将点与平面相关联，然后计算另一个重投影误差。如果两个重投影误差相似，并且最大重投影误差低于某个阈值，则认为该点是平面点。如果一个点多次未能通过几何一致性检查，则将其从候选点集合中删除。

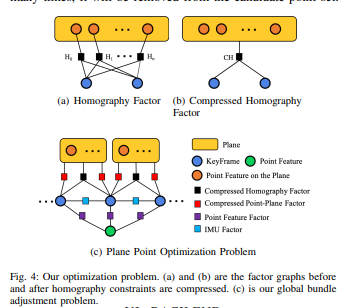
图4.我们的优化问题。(a)和(b)是压缩单应性约束前后的因子图。©是我们的全局BA问题。

6. 后端优化

6.1 测量值

IMU和点特征测量：连续两个关键帧之间的IMU数据使用预积分方法处理[8]，[9]。我们定义了基于预积分的IMU数据的代价项，与[9]相同。由于深度图有效，我们将深度信息集成到视觉点特征测量中。

…详情请参照古月居