🦁 前言

狮子最近做的项目都需要使用到JDK1.8，但是狮子常用的JDK版本是11，所以项目都不兼容！！！经过多方打探，终于发现了不改变原来环境的情况下，在新项目使用JDK1.8，特此发个文章记录一下。

🦁 基础环境

Windows: 10 家庭中文版
IDEA: 2020.2.4
JDK版本：11
JDK新增版本：1.8

🦁 安装JDK1.8

Ⅰ. 下载

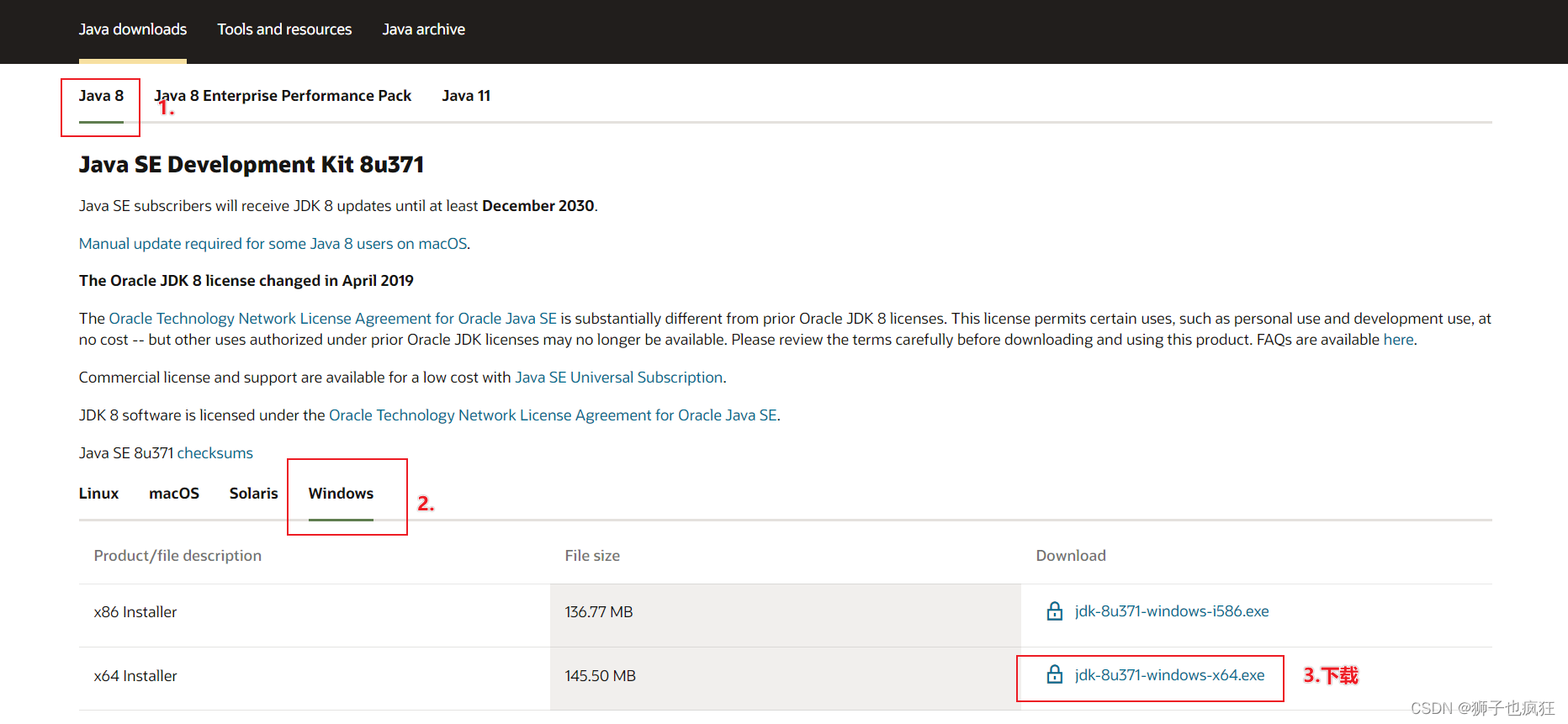
好，现在我们先来新增一个JDK版本，官网下载（需要登录）

1. 点击Products
   
2. 拉到最后，点击Java
   
3. 点击立即下载Java，就可以进入选择版本了
   
4. 下载
   

Ⅱ. 安装

1. 双击.exe文件，一直点击下一步，期间有需要更换安装路径的，根据自己的需要更换即可。

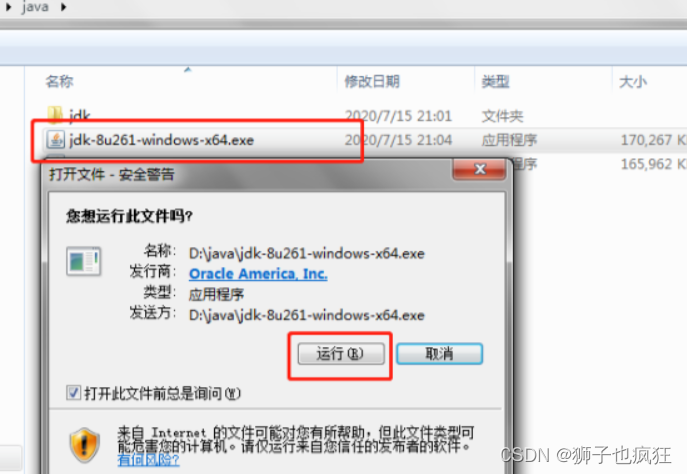
到这里就算安装完成了，不要改动计算机——系统属性——高级系统设置——高级——环境变量

🦁 在项目里更改JDK版本

1. 打开自己不同环境变量的Java项目，打开Project Structure——>Modules——>Sources
   更改Language level为：8 - Lambdas, type annotations etc.
   

2. 然后点击右上角的Project Structure——>Modules——>Dependences
   更改JDK为1.8
   

3. 打开File——>Settings——>Build——>Java Compiler，更改Module下方文件版本为8
   

这样你的环境就改好啦，还不会冲突！！！

---------------------------------------------福利在下面--------------------------------------------------

🦁 福利（送书两本）.

1. 《ChatGPT时代：ChatGPT全能应用一本通》

在AI时代，善用chatgpt会给生活和工作带来很大的帮助，现在狮子来给大家推荐一本书，为您更好地掌握chatgpt科技，如下图：

这本书的好处

• 实用性强：本书通过实际案例和操作技巧，使读者能够快速上手并灵活运用ChatGPT技术，提升职场竞争力。
• 深入浅出：本书以通俗易懂的语言解释ChatGPT的原理和应用，即使是职场新手也能轻松掌握。
• 高效学习：本书结构紧凑，内容精炼，便于读者快速吸收和理解，无需花费大量时间。
• 融合行业经验：本书结合了作者多年的经验，为读者提供了独到的见解和实用建议。

2. 内容简介

本书从ChatGPT等自然语言大模型基础知识讲起，重点介绍了ChatGPT等语言大模型在生活中的实际应用，让每一个人都能了解未来的生活和工作。
本书分为16章，涵盖的主要内容有人工智能、OpenAI、ChatGPT的介绍、ChatGPT的使用技巧，向大家展现ChatGPT在学术教育、商业管理、新媒体、办公、求职、法律、电商等不同领域的应用，以及ChatGPT当下的问题、大模型的未来。
本书通俗易懂，用最简单的语言解释人工智能的入门知识，案例丰富，实用性强，适合每一个想要了ChatGPT等自然语言处理大模型的读者和进阶爱好者阅读，也适合想要通过API打造新时代语言模型应用的开发者。

3. 作者简介

江涵丰，10年科技行业从业者，科技/人工智能领域知名自媒体人。北美工商管理学硕士，获麻省理工人工智能与商业战略相关认证，注册供应链管理师。曾是硅谷科技企业运营管理层，后担任前亚洲第一科技展会CES Asia项目主管，拥有丰富的北美与国内科技行业市场研究、运营管理、数字营销等领域的理论基础和实战经验。
当当自营购买链接：http://product.dangdang.com/29564315.html

---

🦁 抽奖活动 🦁

本次活动赠书2本，评论区抽取2位小伙伴送书

活动时间：截止到 2023-6-13 10：00
参与方式：点赞、收藏本文章，并评论“人生苦短，我用AI !!!”
抽奖时间：2023.6.13
公布时间：2023.6.13
通知方式：交流群内公布或私信通知