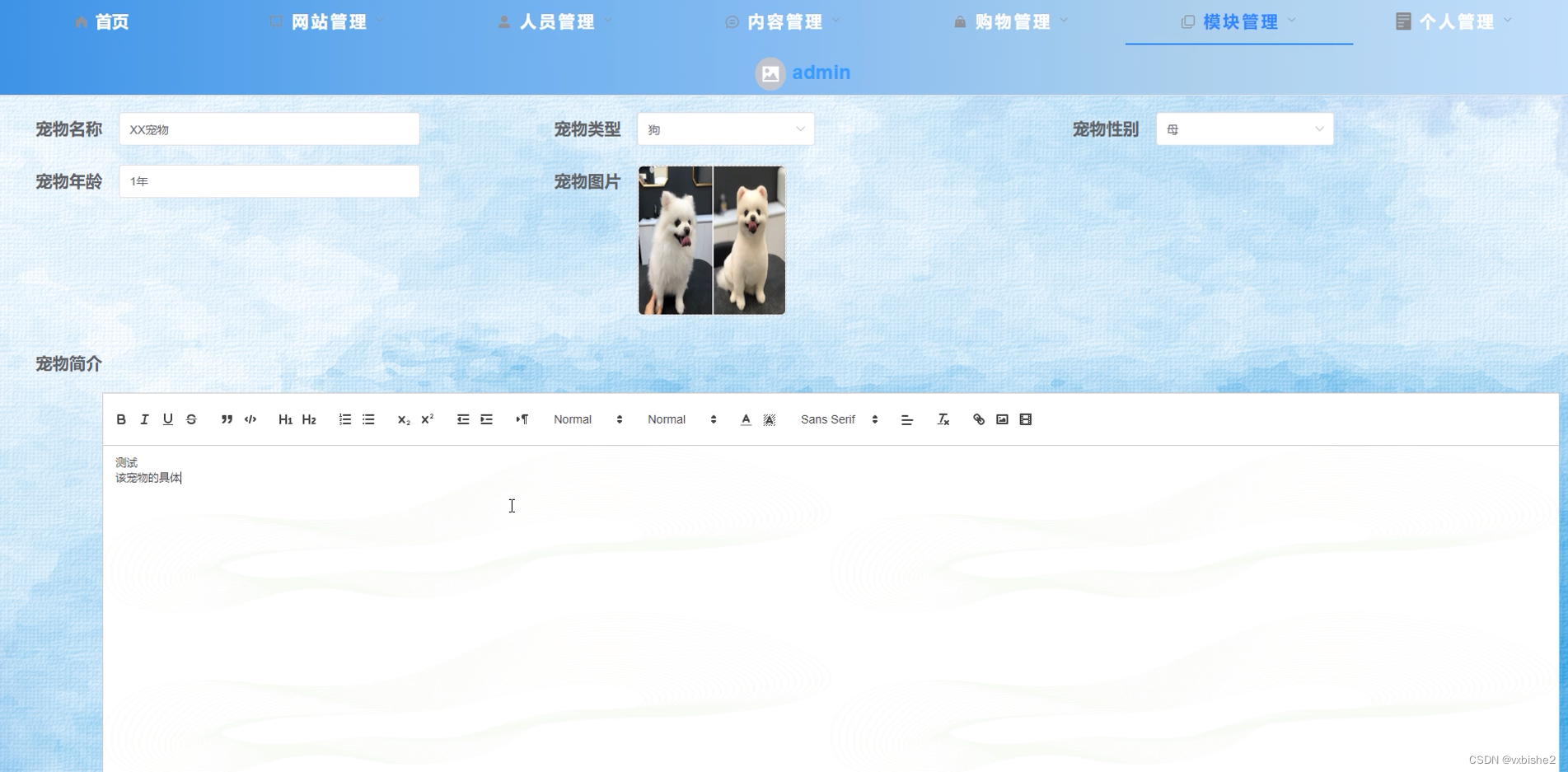
预测模型-灰色预测模型

- 灰色预测是对既含有已知信息又含有不确定信息的系统进行预测,就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
- 灰色预测对原始数据进行生成处理来寻找系统变动的规律,并生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展超势的状况。
灰色预测模型
-
灰色预测模型(Gray Forecast Model)是通过少量的、不完全的的信息,建立数学模型并做出预测的一种预测方法.当我们应用运筹学的思想方法解决实际问题,制定发展战略和政策、进行重大问题的决策时,都必须对未来进行科学的预测.预测是根据客观事物的过去和现在的发展规律,借助于科学的方法对其未来的发展趋势和状况进行描述和分析,并形成科学的假设和判断。
-
灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论.灰色预测是对灰色系统所做的预测。
目前常用的一些预测方法(如回归分析等),需要较大的样本,若样本较小,常造成较大误差,使预测目标失效。灰色预测模型所需建模信息少,运算方便,建模精度高,在各种预测领域都有着广泛的应用,是处理小样本预测问题的有效工具。 -
灰色系统理论是由华中理工大学邓聚龙教授于1982年提出并加以发展的。二十几年来,引起了不少国内外学者的关注,得到了长足的发展。目前,在我国已经成为社会、经济、科学技术在等诸多领域进行预测、决策、评估、规划控制、系统分析与建模的重要方法之一。特别是它对时间序列短、统计数据少、信息不完全系统的分析与建模,具有独特的功效,因此得到了广泛的应用.
灰色系统
- 白色系统
系统的信息是完全明确的。 - 灰色系统
系统的部分信息已知吗,部分信息未知。 - 黑色系统
系统的内部信息是未知的。 - 灰色系统特点:
(1)用灰色数学处理不确定量,使之量化.
(2)充分利用已知信息寻求系统的运动规律.
(3)灰色系统理论能处理贫信息系统.
GM(1,1)模型概述


建模过程




模型检验


模型结果分析

灰色预测模型的使用要点


案例

GM(1,1) code
function gm11 = GM11_model(X,td)
%GM11_model用于灰色模型c(1,1)的建立和预测
%输入参数x为原始数据,td为未来预测期数
%输出参数gm11为一个结构体,包括。
%Coeff_a为发展系数,Coeff_u为灰作用量,
%Predict_Value为预测值,包括当前值和未来td期预测值
%AbsoluteBrror为绝对误差,RelativeErrorMean为相对误差均值
%C为方差比,P误差为小概率,R为关联度
%% 输入参数的控制与默认值
if nargin < 2
warning('输入参数为2个,td将默认使用默认值5')
td = 5;
elseif td < 0
warning('未来预测期数td不能为负值,td将默认使用默认值0')
td = 0;
end
%%数据预处理:累加,平均
n = length(X); %%获取原始数据个数
Ago = cumsum(X); %% 原始数据一次累加 获取新1-AGO序列xi(1)
% Z(i) 为xi(1)的紧邻均值生成序列
% Z = (Ago(1:n-1)+Ago(2:end))/2;
Z = (Ago(1:end-1) + Ago(2:end) ) / 2; % 计算紧邻均值生成数列(长度为n-1)
%%构造B和Ynz矩阵
Yn = X(2:end)'; %Yn是常数项向量 X(2),x(3)
B= [-Z;ones(1,n-1)]'; %% 累加生成数据作均值
%% 最小二乘法求解发展系数a和灰色作用量u
LS_solution = (B'*B)\(B'*Yn); %% 利用公式求解a,u
a = LS_solution(1); %%发展系数a
u = LS_solution(2); %%灰色作用量u
%%建立灰度GM(1,1)模型,白化一元一阶微分方程
F = [X(1),(X(1)-u/a)./exp(a*(1:n+td-1))+u/a];
%% 还原序列,得到预测数据
PreData = [F(1),F(2:end)-F(1:end-1)];
%% 数据可视化
t = 1:n;
plot(t,X,'ko-','MarkerFaceColor','k') %%原数据图像
hold on;
grid on
%%预测当前数据图像
plot(t,PreData(1:n),'b*-','LineWidth',1.5)
%% 未来td期数据图像
plot(n:n+td,PreData(n:n+td),'r*-','LineWidth',1.5)
title('GM(1,1) model --- Original VS Current And Future Predict');
legend('OriginalData','ForecastData','ForecastFutureData','Location','best')
legend('boxoff')
set(get(gca, 'XLabel'), 'String', 'Time');
set(get(gca, 'YLabel'), 'String', 'Value');
%% 模型校验
Err = abs(X-PreData(1:n)); %真实值与预测值误差
q = mean(Err./X);%真实值与预测值误差
XVar = std(X,1);%原数据的标准方差,前置因子1/n
ErrVar = std(Err(2:end):1);%残差(2:end)的标准方差,前置因子1/n
C = ErrVar/XVar; %后验方差比
%小误差率
P = sum(abs(Err-mean(Err))<0.6745*XVar)/n;
R_k = (min(Err)+0.5*max(Err))./(Err+0.5*max(Err)); %rho=0.5
R = sum(R_k)/length(R_k); %关联度
%%计算变量组合,生成输出结构体变量
gm11.Coeff_a = a;
gm11.Coeff_u = u;
gm11.Predict_Value = PreData;
gm11.AbsoluteError = Err;
gm11.RelativeErrorMean = q;
gm11.R = R;
gm11.C = C;
gm11.P = P;
end
X = [174,179,183,189,207,234,220.5,256,270,285,300,320,344,365];
gm11 = GM11_model(X,5)
%%未来预测值
prd = gm11.Predict_Value(end-5+1:end)
%{
gm11 =
包含以下字段的 struct:
Coeff_a: -0.0621
Coeff_u: 156.7876
Predict_Value: [1×19 double]
AbsoluteError: [0 6.1049 0.9646 6.7429 1.2753 12.3899 15.2986 5.1045 3.0410 0.9490 2.2373 1.5880 1.8225 0.9147]
RelativeErrorMean: 0.0185
R: 0.7182
C: NaN
P: 1
根据模型评价标准
p=1,C=0.0724,预测等级为:好;
相对误差均值0.085,合格
关联度0.7182,勉强合格
由于-a系数小于0.3,适合中长期预测。
从运行结果看,对于线性的数据使用GM(11)预测,其拟合效果还是不错。
%%未来预测值
prd =
387.3958 412.1987 438.5896 466.6702 496.5486
%}
![Linux学习[19]管线命令详解1---cut, grep, sort, wc, uniq](https://img-blog.csdnimg.cn/19f1fdcb7adc4fd0b8096e8968165879.png)