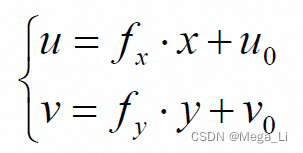计算物理专题：主值积分

• 吴式枢理论

主值积分

• 设在以及上可积，其中为任意小的正数，当两者独立地趋于零，极限存在。如果，这个极限存在，则称它为瑕积分的主值，记作
• 无界函数的改造
• 则该瑕积分的主值为：

• 结合起来即得函数积分的主值公式

寻找瑕点

        with warnings.catch_warnings():
            warnings.filterwarnings("error")

with warnings.catch_warnings() :创建一个上下文管理器，用于临时控制警告的行为

warnings.filterwarnings("error") :设置警告过滤器为"error"，这意味着将所有的警告都转换为异常

import numpy as np
import warnings

def Divergent_points(f,a,b,h=0.01,threshold=10000):
    
    x = np.arange(a,b+h,h)
    #print(x)
    divergent_points = []
    for xi in x:
        with warnings.catch_warnings():
            warnings.filterwarnings("error")
            try:
                a = f(xi)
                if abs(a) >= threshold:
                    divergent_points.append(xi)
            except RuntimeWarning:
                divergent_points.append(xi)
            except (ZeroDivisionError, OverflowError):
                divergent_points.append(xi)
    return divergent_points


f = lambda x:1/(x-3.0)/(x-3.4)
a = 2.9  
b = 3.42 

divergent_points = Divergent_points(f,a,b)
print("瑕点：",divergent_points)

主值积分的计算设计

#龙贝格积分
def Romberg(f, a, b, n=4):
    R = np.zeros((n, n))
    h = b - a
    R[0, 0] = (f(a) + f(b)) * h / 2
    for i in range(1, n):
        h /= 2
        sum_f = 0
        for k in range(1,2**i,2):
            sum_f += f(a+k*h)
        R[i,0] = 0.5*R[i-1,0] + sum_f*h
        for j in range(1,i+1):
            R[i,j] = R[i,j-1] + (R[i,j-1]-R[i-1,j-1])/(4**j-1)
    return R[n-1, n-1]

def VP_integration(f,a,b,epr=100000):
    eprsilon=(b-a)/epr
    divergent_points = Divergent_points(f,a,b)
    print("瑕点：",divergent_points)

    Sum = 0
    for k in divergent_points:
        Sum += eprsilon * (f(k+eprsilon)+f(k-eprsilon))
        
    divergent_points.append(b)
    divergent_points.insert(0,a)
    new_list = [divergent_points[0]]
    for i in range(1, len(divergent_points)-1):
        new_list.append(divergent_points[i] - eprsilon)
        new_list.append(divergent_points[i] + eprsilon)
    new_list.append(divergent_points[-1])

    print("new_list",new_list)
    Num = len(new_list)
    for i in range(0,Num,2):
        c = Romberg(f,new_list[i],new_list[i+1])
        Sum += c
        print("Romberg:",c)        
    
    return Sum

f = lambda x:x*np.sin(x)*np.cos(x)/(x-3.0)
a = 1
b = 5
I = VP_integration(f,a,b)
print(I)

•  提示：我们一般选择积分区间的10w分之一作为eprsilon(epr)
• 主值积分方法不同，得出的结论也不太同，比如使用mma的结果：

•  相信自己，mma在处理主值积分这方面效果确实不好。

自适应光学概述

        传统的光学技术无法解决动态波前扰动对光波质量的影响。1953年，美国天文学家H.W.Babkock 提出了Adaptive Optics 的概念。自适应光学技术现已应用在天文学，空间光学，激光，生物等领域。自适应光学系统器件主要包括波前校正器，波前传感器和波前控制器。

        波前校正器通过改变折射率与光路长度实现波前校正，分为 Tip-Tile Mirror 与 Deformable Mirror两大类。Tip-Tile Mirror 用于波前畸变整体倾斜校正，Deformable Mirror可用于校正高阶项畸变。

        波前传感技术分为直接测量与间接测量两类。直接测量通过测量波前斜率或者测量波前曲率获得波前相位信息。1972年，R.N.Smartt 提出了点衍射干涉仪，可以直接测量波前的相位分布。点衍射干涉仪的光能利用率较低，只适用于发射强激光的自适应光学系统。

        间接波前测量法通过测量与光波波前存在一定数学关系的物理量间接获得波前信息。1972年，Gerchberg-Saxton 提出从已知像平面和衍射平面上的光强分布计算出两个平面上的相位分布的GS算法。

        波前控制器接收和处理波前传感器的输出信息，输出校正波前信号。1979年，R.Cubalchini 提出了用Zernike多项式重构波前的算法。

自适应光学在天文观察中的应用

        1998年，美国国家太阳天文台的Rimmele等研制了第一个实用化的太阳自适应光学系统，该系统实现了以太阳米粒结构为信标的自适应光学校正。2009年成都光电技术研究所将37单元自适应光学系统用于云南天文台的26cm精细结构望远镜中，获得了高分辨率的太阳表面图像。[]2017年，中科院光电技术研究所研究员使用多层共轭自适应光学技术获得了对太阳活动区的大视场高分辨力实时图像，提高了对太阳爆发性活动的预警预报能力[]。

        随着深度学习技术的快速发展，自适应光学的盲复原有了更多的选择。一种全新的基于动态滤波网络的自适应光学图像盲复原方法更好得解决了移除空变模糊的问题。其中的时空卷积神经网络PPL-STCNN不仅可以移除已知模糊，也可以很好的移除未知模糊，提升了基于自适应光学的地基太阳观察的观测性能。

        1985年, 首次有人提出了人造激光导引星应用于天文自适应观测的概念。自适应光学系统需要足够亮度的导引星作为波前探测的信标, 可以利用目标本身作为信标, 也可以在目标的等晕区范围内寻找一颗合适亮度的自然导引星作为信标, 这样的系统称为自然导引星自适应光学系统。

自适应光学在生物成像中的应用

        2002年，Rooda等首次将自适应光学技术应用与飞点电视检眼镜，用以校正人眼的高阶像差。2011年，程少园等提出了一套液晶自适应光学扫描激光检眼镜的光学系统。[]该系统能较好得消除人眼像差与光学系统自身的像差，能使得观测水平接近系统的衍射极限。

        荧光显微成像技术通过观察和追踪活体内不同尺度的荧光信号，获得活体组织内小分子的位置，结构，变化等信息。荧光显微成像技术像差主要有三个来源：显微镜盖玻片与样本承载介质之间的折射，样本厚度，光学元件。

        双光子显微成像中，波前像差的存在导致荧光信号强度和空间分辨率下降。2016年，哈尔滨工业大学针对单层折射率不匹配球差和多层折射率不匹配问题分别提出了两套矫正方案，提升了荧光处理方法的检测效率[]。        

自适应光学在惯性约束可控核聚变中的应用

        惯性约束聚变驱动器对焦斑形态具有特殊的要求。自适应光学作为一种成熟的相位控制技术，基于衍射叠加原理，通过建立一种新型压电薄膜变形镜，应用G-S算法可以较好得解决这个问题。[]

1.2.3.1远场评价参数

        定义实际焦斑与目标焦斑的RMS差值，用来描述焦斑轮廓相似性，该值越小，说明实际焦斑与目标焦斑轮廓相似度越高，表达式为。。。

        在ICF过程中，必须尽可能实现靶面均匀辐照，因此焦斑均匀性也是评价ICF驱动装置性能的重要指标。n表示平均光强的倍数。在间接驱动中，一般用超过概率密度的统计曲线来描述焦斑的均匀性：

变形镜和哈特曼波前探测器的Matlab仿真

        波前校正器对入射的畸变波前进行校正补偿畸变，是自适应光学系统的核心器件。常见的波前校正器一般有空间光调制器和变形镜（DM）两种。

        变形镜通过改变反射面的形状对波前进行校正（即光程差中的传播路径），空间光调制器通过改变材料折射率改变光程。反射的过程中能量损失较少，因此变形镜更适用于光强较低的情况。根据反射面的类型，可以将变形镜分为分段式和连续式两种。

        连续式DM由一个连续的反射镜薄膜和薄玻璃组成，镜面的背面与驱动器相连，以推、拉的方式使与其相连的薄镜面产生形变。连续式DM缺点是相邻驱动器间存在的耦合使驱动器之间的控制复杂化。某一个驱动器作用会使得相邻位置处的镜面也会有一定的形变。

        分段式DM每个驱动器的末端都由可独立控制的微小反射镜组成，因此更适合校正具有更高空间频率的像差。由于相邻镜子之间没有相互作用，故分段式DM具有零耦合的性质。

        可以使用二维高斯函数来描述变形镜驱动器的响应函数

大气湍流效应

        地球各维度受到的太阳辐射差异，昼夜更替等因素使得大气层流在部分转化为湍流运动并形成相应的涡旋。湍流大气中，温度，湿度，气压等参数的变化周期小则毫秒大则几天，几年甚至更长。一般用一些表征参数来描述大气湍流的特征，如相位结构函数，大气相干长度，等晕角以及相位功率谱密度1。

1.4.1相位结构函数。

        相位结构函数表示相位空间平面上两点间光程差的统计信息，是分析湍流波前相位的重要参数。

1.4.2大气相关长度

        大气相干长度是反映大气湍流强度的一个特征尺度，用于表征波前相位的空间相干尺度。对于平面波，大气相干长度可以表示为

        其中，的物理意义是任何光学系统对经过大气湍流的光波成像，其分辨率不会超过口径为的光学系统的衍射极限分辨率。光波波长越长，越大。因此自适应光学系统在红外波段校正要比在可见光波段校正更容易实现。

        表示积分路径所对应的天顶角，即入射光线与天顶方向的夹角。

        表示折射率结构常数，总体上随着高度的增加而减小，一般需要通过实验测量来描述。其在一定程度上反应了大气湍流的程度。越大，湍流越长。

等晕角

        激光相位差依赖于大气环境的诸多特性。依赖于天顶角的特性被称为大气的非等晕性。若依据空间中两点的相位差能否近似于与天顶角无关，从而将大气中的一小部分与其他部分割裂开来，这一小部分则被称为等晕区。

        等晕角指的是两个夹角为 的目标发出的光经过大气湍流同时到达接收孔径，不同路径引入的光波相位差方根值小于1rad时所对应的夹角。对于Kolmogorov湍流，等晕角的表达式为

大气激光通信概述

        在大气激光通信中，信号被加载到激光上在大气环境中进行传输。大气激光通信具有传输速率高、保密性好、指向性好等特点，可以被用于地面通信、卫星通信等领域。光信号在大气信道中传输时，容易受到大气湍流效应等的影响发生功率衰减，光束漂移，波前畸变等劣化通信质量的事件。

        目前，大气激光通信技术面临的最紧要问题就是大气通信中湍流对光信号的影响。自适应光学技术正加入到激光通信系统中以改善大气湍流扰动的影响。