论文:https://arxiv.org/abs/2012.11879
中文版:FcaNet: Frequency Channel Attention Networks
源码:https://github.com/cfzd/FcaNet或https://gitee.com/yasuo_hao/FcaNet
一、论文背景和出发点
问题:许多工作都集中在如何设计高效的通道注意机制上,而忽略了一个基本问题,即由于大量的信息丢失,通道注意机制使用标量来表示通道会很困难。(传统的GAP操作,即“平均”操作会极大的抑制特征的多样性,而且会造成大量信息的丢失。)
出发点:在这项工作中,我们从不同的角度出发,将信道表示问题视为使用频率分析的压缩过程。基于频率分析,我们从数学上证明了传统的全局平均池是频域特征分解的一个特例。(为使用离散余弦变换压缩信道提供了可能性。)
有了这些证明,我们自然地推广了信道注意机制在频域中的压缩,并提出了我们的多谱信道注意方法,称为FcaNet。(传统的GAP操作压缩通道的效果不好,因此作者提出使用离散余弦变换(DCT)来压缩信道。)
简单地来说,作者将通道注意力视为一个压缩问题,传统的方式使用全局平均化池会造成大量信息丢失,所以作者建议在信道注意力机制中使用离散余弦变换(DCT)来压缩通道。
二、创新点
1. 证明了传统GAP(全局平均化池)是DCT(离散余弦变换)的特例。
2. 提出了三种频率分量选择标准以及建议的多光谱信道注意力框架,以实现FcaNet。
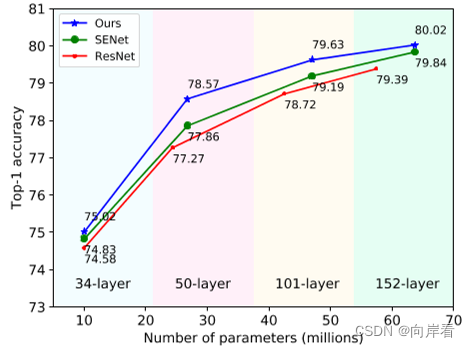
3. 大量实验表明,该方法在ImageNet和COCO数据集上都取得了最先进的结果,计算成本与SENet相同。在ImageNet数据集上的结果,如下图所示:
三、离散余弦变换(DCT)和通道注意力
1. 离散余弦变换DCT
作用:
(1)2维DCT的基函数
![]()
(2)2维DCT
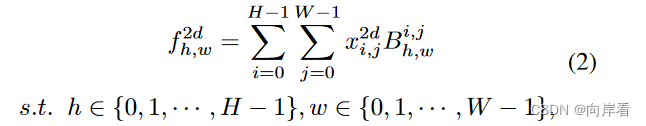
其中是2维DCT频谱,
是输入图像,
是
的高度,
是
的宽度,
是2维DCT的基函数,
∈ { 0, 1, · · · , H−1 },
∈ { 0, 1, · · · , W−1 }。
(3)逆2维DCT
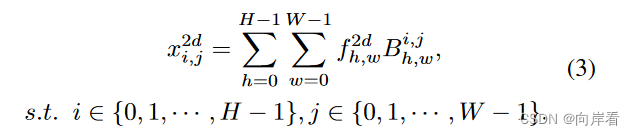
2. 通道注意力
传统方式的阐述,以SE模块为例。
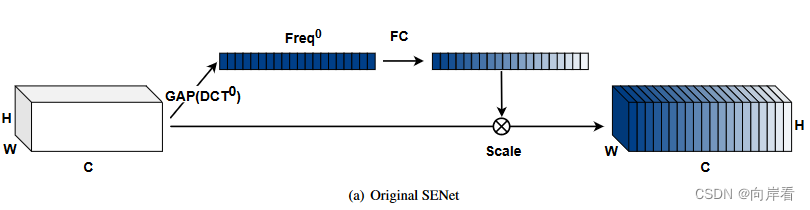
(1)注意力向量
![]()
其中,是注意力向量,sigmoid是sigmoid函数,
代表映射函数,如全连接层或一维卷积,
是一种压缩方法(SE模块中使用全局平均池化GAP)。详情可参考:SENet的Squeeze操作和Excitation操作。
(2)缩放
在获得所有通道的注意力向量后,输入X的每个通道按相应的注意力值进行缩放:
![]()
其中,X̃是注意力机制的输出,是注意力向量的第i个元素,
是输入图像的第i个通道。详情可参考:SENet的Scale操作。
3. 证明:GAP是2D-DCT的特例
将2维DCT公式中的h和w都置为0,得到:
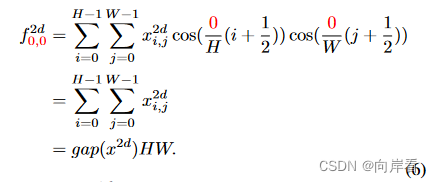
表示最低频率分量与gap函数成正比,由上式可见,gap函数是2维DCT的一种特例。
结论:在信道注意机制中使用GAP意味着只保留最低频率的信息。
推广:除了低频信息以外,其他频率的所有分量也表示信道的有用信息不应被遗弃,所以作者提出在注意力机制中将GAP推广到2D DCT,并用2D DCT的多个频率分量压缩更多信息。
四、Multi-Spectral Channel Attention的具体实现
多光谱通道注意力模块,如下图所示:
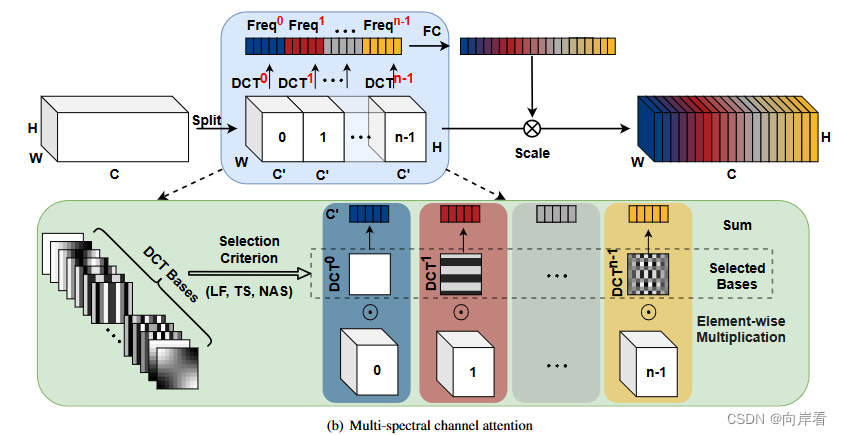
1. 分割
沿通道维度方向将输入分成
。
其中,,通道数C被分为了n份。
2. 压缩
对于每个,分配相应的2D-DCT频率分量用作每个
的压缩,得到的
构成通道注意力的各个分量。
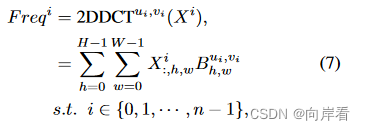
其中,是对应于
的频率分量2维指数,
是压缩后的C'维向量。
3. 拼接
对每个进行拼接操作,得到多光谱向量。
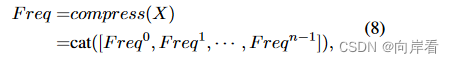
其中,是获得的多光谱向量。
4. 多光谱通道注意力
为了获取通道注意力,多光谱向量还要经过全连接层和sigmoid处理。整个多光谱通道注意力框架可以表示为:
![]()
获取到通道注意力之后的步骤与SEnet基本一致。
五、频率分量的选择标准
如何为每个选择频率分量指数
是一个重要问题,作者提出了三个选择标准。
1. FcaNet LF(低频)
只选择低频分量。
2. FcaNet TS(两步选择)
第一步:分别评估通道注意力中每个频率分量的结果。
第二步:根据评估结果,我们选择了性能最高的Top-k频率分量。
3. FcaNet NAS(神经结构搜索)
使用神经结构搜索来搜索信道的最佳频率分量。
对于每个,将一组连续变量
配给搜索组件。该
的频率分量可以表示为:
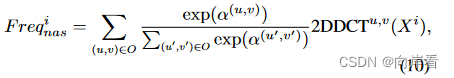
其中O是包含所有2D DCT频率分量索引的集合。训练后,的频率分量等于
中的最大值。
六、实验
数据集:ImageNet,COCO数据集。
网络:ResNet-34、ResNet-50、ResNet-101和ResNet-152。
1. 在ImageNet上不同注意力方法的比较
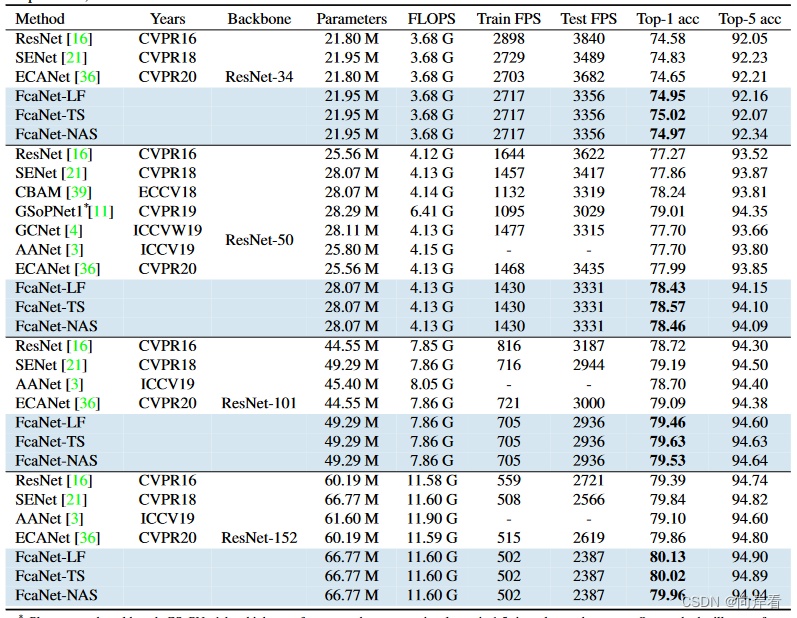
在相同的计算成本下,FcaNet优于对比的不同注意力方法。
2. 在CoCo上不同注意力方法的比较
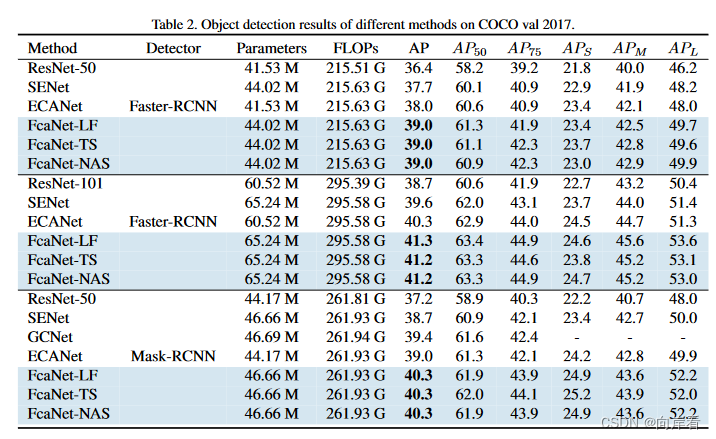
在不同的数据集上,FcaNet依然优于对比的不同注意力方法。
七、总结
在本文中,研究了通道注意力的一个基本问题,即如何表示通道,并将此问题视为一个压缩过程。证明了GAP是DCT的一个特例,并提出了具有多谱注意力模块的FcaNet,它在频域上推广了现有的信道注意力机制。同时,在多谱框架中探索了频率分量的不同组合,并提出了频率分量选择的三个标准。在相同数量的参数和计算成本的情况下,本文提出的方法可以始终优于SENet。与其他通道注意力方法相比,我们在图像分类、对象检测和实例分割方面也取得了最先进的性能。此外,FcaNet简单而有效。本文提出的方法可以在现有信道注意力方法的基础上,只需更改几行代码即可实现。