编者按:
本文提出了一种包含供需交互作用的航空网络规划模型 (ANPSD),该模型同时考虑了航线选择、航班频率和机队组成等问题,还捕捉了航空公司的供应和乘客需求之间的相互依赖关系。作者将需求实证函数与 ANPSD 模型相结合,开发了一种名为 2𝛼ECP 的精确割平面算法来解决此混合整数非凸优化模型,并针对一家欧洲航空公司的网络进行案例分析。
1. 引言
在过去的几十年里,航空业在全球范围内高速发展,但同时也面临着各种外部冲击所带来的需求波动方面的挑战。本文在战略层面提出了一种考虑供需交互作用的航空网络优化模型 ANPSD (Airline Network Planning with Supply and Demand interactions)。它首先从人口、地理、经济等角度出发,利用两阶段最小二乘法得到了一个实证模型来估计乘客需求。其次本文在考虑路线选择,航班频率以及机组构成等问题的基础上,融入乘客需求函数,从而开发出一种新型的航空网络优化模型。文章证明了此模型的非线性与非凸性后,运用一种基于外部近似的精确割平面算法来对此进行求解,结果表明此算法能在较短的时间内返回比基准更优质的方案。最后,作者将该模型应用于意大利航空公司的大陆网络,并从管理的角度提供了关于如何平衡相互竞争的网络规划目标的战略见解。
2. 模型描述

如Fig. 1所示,该建模框架包括两个主要元素:需求模型和优化模型。
2.1 需求模型
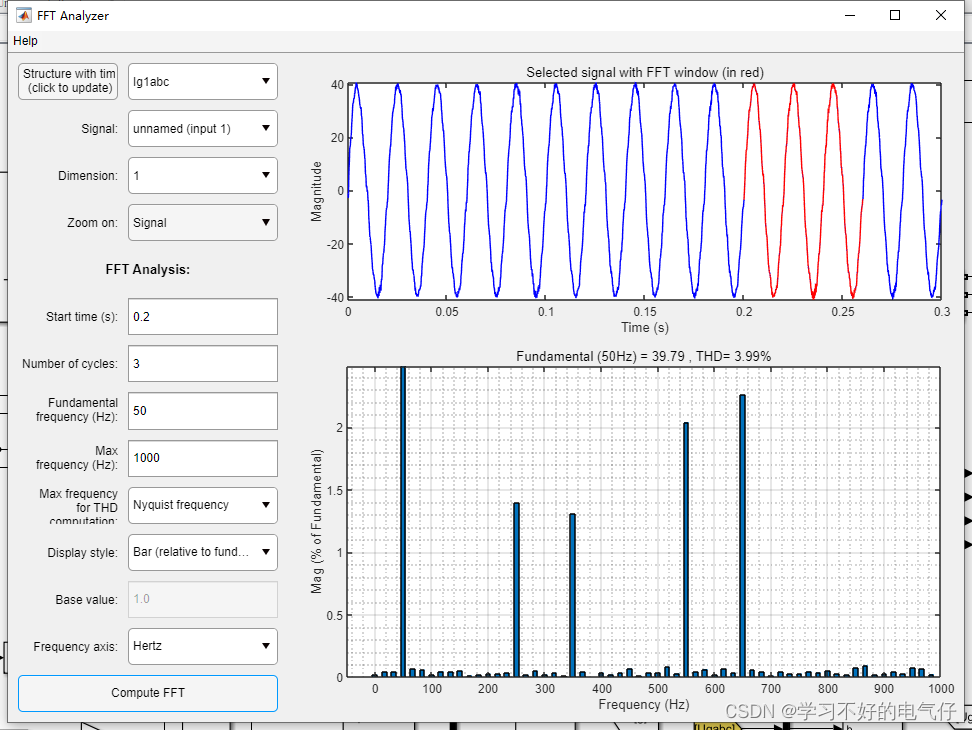
需求模型将航班时刻表、机票价格、客流和社会经济变量的历史数据作为输入。 它使用两阶段最小二乘法和工具变量来估计每个航段的每月乘客需求,其中包括直达和转机乘客,以解决内生性问题。(1)式是作者得出的需求函数,其捕捉了乘客需求与服务频率和网络结构大小(由辐条数量代表)的依赖关系。 D = γ f u s v ( 1 ) D = \gamma f^u s^v \quad (1) D=γfusv(1)
其中 D D D是需求, γ \gamma γ是包括截距和所有剩余的解释变量的参数, f f f是飞机服务频率, s s s是辐条数量, u , v u,v u,v是弹性参数估计值。
2.2 优化模型
该航空网络优化决策模型 ANPSD 考虑了包括航线选择、航班频率和机队构成等因素,站在具有轴辐式 (Hub-and-spoke) 结构的单个航空公司的视角,使其利润最大化。
ANPSD 从定义一个完整的潜在网络开始,其特征是一组机场节点集合 ( N ) (\mathcal{N}) (N),包括枢纽机场 ( H ) (\mathcal{H}) (H)和辐射机场,以及一组候选航段集合 ( I ) (\mathcal{I}) (I)。在机队方面,ANPSD 考虑了具有特定飞机规格的机队类型集合 ( A ) (\mathcal{A}) (A)以及飞机规格。除此之外作者用 ( t i a ) (t_{ia}) (tia)表示航班 a a a在航段 i i i的总飞行时间, 用 ( k a ) (k_{a}) (ka)定义每架飞机 a a a的的座位容量。 用 ( l a ) (l_{a}) (la)定义了飞机 a a a的最长使用时间。 为估算运营盈利能力,ANPSD 需要了解机票价格和运营成本。因此本文运用 ( p i ) (p_{i}) (pi)表示航线 i i i的票价,运用 ( c i a v a r ) (c^{var}_{ia}) (ciavar)表示可变成本,用 ( c a f i x ) (c^{fix}_{a}) (cafix)表示为固定成本。
该模型的决策变量有:类型
a
a
a的飞机数量
(
w
a
)
(w_{a})
(wa); 飞机类型
a
a
a在每条航线
i
i
i上的频率
(
f
i
a
)
(f_{ia})
(fia);
(
x
i
)
(x_{i})
(xi)是二元变量,用来判断航线
i
i
i是否运营,它与
(
f
i
)
(f_{i})
(fi)和
(
s
i
)
(s_{i})
(si)共同作为需求函数的输入;航线
i
i
i上的载客量为
(
q
i
)
(q_{i})
(qi)。 以下为数学模型表达:
m
a
x
∑
i
∈
I
p
i
q
i
−
∑
i
∈
I
∑
a
∈
A
c
i
a
v
a
r
f
i
a
−
∑
a
∈
A
c
a
f
i
x
ω
a
(
2
)
max \quad \sum_{i \in \mathcal{I}} p_i q_i - \sum_{i \in \mathcal{I}}\sum_{a \in A} c^{var}_{ia}f_{ia} - \sum_{a \in A} c^{fix}_a \omega_a \quad\quad (2)
maxi∈I∑piqi−i∈I∑a∈A∑ciavarfia−a∈A∑cafixωa(2)
目标函数为最大化航空公司的营业利润。
s
.
t
.
∑
i
∈
I
n
o
u
t
f
i
a
=
∑
i
∈
I
n
i
n
f
i
a
∀
n
∈
N
,
∀
a
∈
A
(
3
)
s.t.\quad \sum_{i \in{I}^{out}_n} f_{ia} = \sum_{i \in{I}^{in}_n} f_{ia} \quad\quad \forall n\in\mathcal{N},\forall a\in\mathcal{A} \quad(3)
s.t.i∈Inout∑fia=i∈Inin∑fia∀n∈N,∀a∈A(3)
I
n
o
u
t
\mathcal{I}^{out}_n
Inout和
I
n
i
n
\mathcal{I}^{in}_n
Inin分别代表从机场
n
n
n出发和进入机场
n
n
n的
I
\mathcal{I}
I的子集,约束 (3) 为流量平衡约束。
∑
i
∈
I
f
i
a
t
i
a
≤
l
a
w
a
∀
a
∈
A
(
4
)
\sum_{i \in I} f_{ia}t_{ia} \leq l_a w_a \quad\quad \forall a\in\mathcal{A} \quad(4)
i∈I∑fiatia≤lawa∀a∈A(4)
约束 (4) 确保飞机的总利用率不超过最大可能利用率。
f
i
a
=
0
∀
a
∈
A
i
O
,
∀
i
∈
I
(
5
)
f_{ia} = 0 \quad\quad \forall a\in\mathcal{A}_i^O, \forall i\in\mathcal{I} \quad(5)
fia=0∀a∈AiO,∀i∈I(5)
A
i
O
\mathcal{A}_i^O
AiO表示不能用于在航段
i
i
i飞行的飞机类型
A
\mathcal{A}
A的子集,约束 (5) 确保每个飞机航段组合的可行性。
q
i
≤
∑
a
∈
A
f
i
a
k
a
∀
i
∈
I
(
6
)
q_i \leq \sum_{a\in A} f_{ia} k_a \quad\quad \forall i\in\mathcal{I} \quad (6)
qi≤a∈A∑fiaka∀i∈I(6)
约束 (6) 确保载客数量在飞机的作为容量内。
f i ≤ ∑ a ∈ A f i a ∀ i ∈ I ( 7 ) f_i \leq \sum_{a\in A} f_{ia} \quad\quad \forall i\in\mathcal{I} \quad (7) fi≤a∈A∑fia∀i∈I(7)
约束 (7) 计算出每条航段上的飞机频率。
f
i
−
x
i
≥
0
∀
i
∈
I
(
8
)
f_i - x_i \geq 0 \quad\quad \forall i\in\mathcal{I} \quad (8)
fi−xi≥0∀i∈I(8)
约束 (8) 确保在运营的航段上至少有一架飞机服务。
f i − M x i ≤ 0 ∀ i ∈ I ( 9 ) f_i - Mx_i \leq 0 \quad\quad \forall i\in\mathcal{I} \quad (9) fi−Mxi≤0∀i∈I(9)
约束 (9) 运用大M法确保只有在运营的航段上的飞机服务频率为正。
s i = ∑ n ∈ H ∑ j ∈ I n i n δ i n o u t x j + ∑ n ∈ H ∑ j ∈ I n o u t δ i n i n x j ∀ i ∈ I ( 10 ) s_i = \sum_{n \in \mathcal{H}}\sum_{j \in \mathcal{I}^{in}_n} \delta^{out}_{in} x_j + \sum_{n \in \mathcal{H}}\sum_{j \in \mathcal{I}^{out}_n} \delta^{in}_{in} x_j \quad\quad \forall i\in\mathcal{I} \quad (10) si=n∈H∑j∈Inin∑δinoutxj+n∈H∑j∈Inout∑δininxj∀i∈I(10)
δ
i
n
o
u
t
\delta^{out}_{in}
δinout和
δ
i
n
i
n
\delta^{in}_{in}
δinin都是二元变量,用来确定航段
i
i
i是否从机场
n
n
n起飞或到达机场
n
n
n,等式 (10) 用来计算辐条数。
q
i
≤
γ
i
f
i
u
s
i
v
∀
i
∈
I
(
11
)
q_i \leq \gamma_if_i^us_i^v \quad\quad \forall i\in\mathcal{I} \quad (11)
qi≤γifiusiv∀i∈I(11)
约束 (11) 保证实际容纳乘客数量不超过估计需求。
f
i
a
∈
Z
+
∀
a
∈
A
,
∀
i
∈
I
(
12
)
f_{ia}\in \mathbb{Z}^+ \quad\quad \forall a\in\mathcal{A}, \forall i\in\mathcal{I} \quad (12)
fia∈Z+∀a∈A,∀i∈I(12)
f
i
∈
Z
+
,
x
i
∈
{
0
,
1
}
,
q
i
∈
R
+
,
s
i
∈
Z
+
∀
i
∈
I
(
13
)
f_{i} \in \mathbb{Z}^+, x_i\in\{0,1\}, \thinspace q_i\in \mathbb{R}^+, \thinspace s_i\in \mathbb{Z}^+ \quad\quad \forall i\in\mathcal{I} \quad (13)
fi∈Z+,xi∈{0,1},qi∈R+,si∈Z+∀i∈I(13)
w
a
∈
Z
+
∀
a
∈
A
(
14
)
w_a\in \mathbb{Z}^+ \quad\quad \forall a\in\mathcal{A}\quad (14)
wa∈Z+∀a∈A(14)
(12) - (14) 都是决策变量的值域约束。
3. 求解算法
在约束 (11) 的作用下,经过计算与证明,此模型为非线性非凸问题。在先前的研究中,有学者运用 𝛼 因子矫正了凸函数的基于梯度的线性近似以解决非凸性问题,此方法被称为 𝛼ECP (extended cutting-plane)。在本文中,作者通过一组外部近似半超平面替换约束 (11) 来解决主问题,每次迭代后都会生成两个新的半超平面,并更新上限和下限,最终收敛到 ANPSD 的最优解。作者根据两个离散化基准评估 2𝛼ECP 的计算性能:Convex combination (CC) 与 Logarithmic branching convex combination (LOG) 基准。CC方法直接用一组分段线性超平面来近似非线性函数。LOG方法将非线性函数逼近为离散点的凸组合,此方法关键点在于其用许多二元变量和约束条件重新表述了凸组合,这些变量和约束条件随或多面体的数量呈对数增长。数值实验表明,2𝛼ECP 算法与基于离散化和线性化的最新基准相比,实现了更强、更稳定和更一致的性能。 此外,它也是一种精确方法,它在每次迭代时提供最优性的解决方案,而不是仅生成可行的解决方案。
4. 案例分析
本文通过对意大利航空公司大陆网络进行案例研究,强调了在航空公司网络规划中考虑供需相互作用的优势,并展示了如何运用 ANPSD 模型进行有关飞行网络和机队内生扩张(或收缩)的战略决策。为了证明在航空公司战略规划中整合供需交互的好处,作者采用三种不同的需求模型。
i
)
i)
i):
P
0
\mathcal{P}_0
P0忽略供需相互作用,需求被视作固定参数,用
q
i
≤
D
i
ˉ
q_i \leq \bar{D_i}
qi≤Diˉ来代替约束 (11)。
i
i
)
ii)
ii):
P
1
\mathcal{P}_1
P1忽略中心辐射网络效应产生的积极影响,用
q
i
≤
γ
i
′
f
i
u
′
q_i \leq \gamma^\prime_if^{u^{\prime}}_i
qi≤γi′fiu′来代替约束 (11)。
i
i
i
)
iii)
iii)模型 ANPSD。通过改变路线数量 (
△
n
t
w
\triangle ntw
△ntw) 与机队规模 (
△
f
l
e
e
t
\triangle fleet
△fleet),作者采用九种情景来对三种模型的性能进行比较评估。
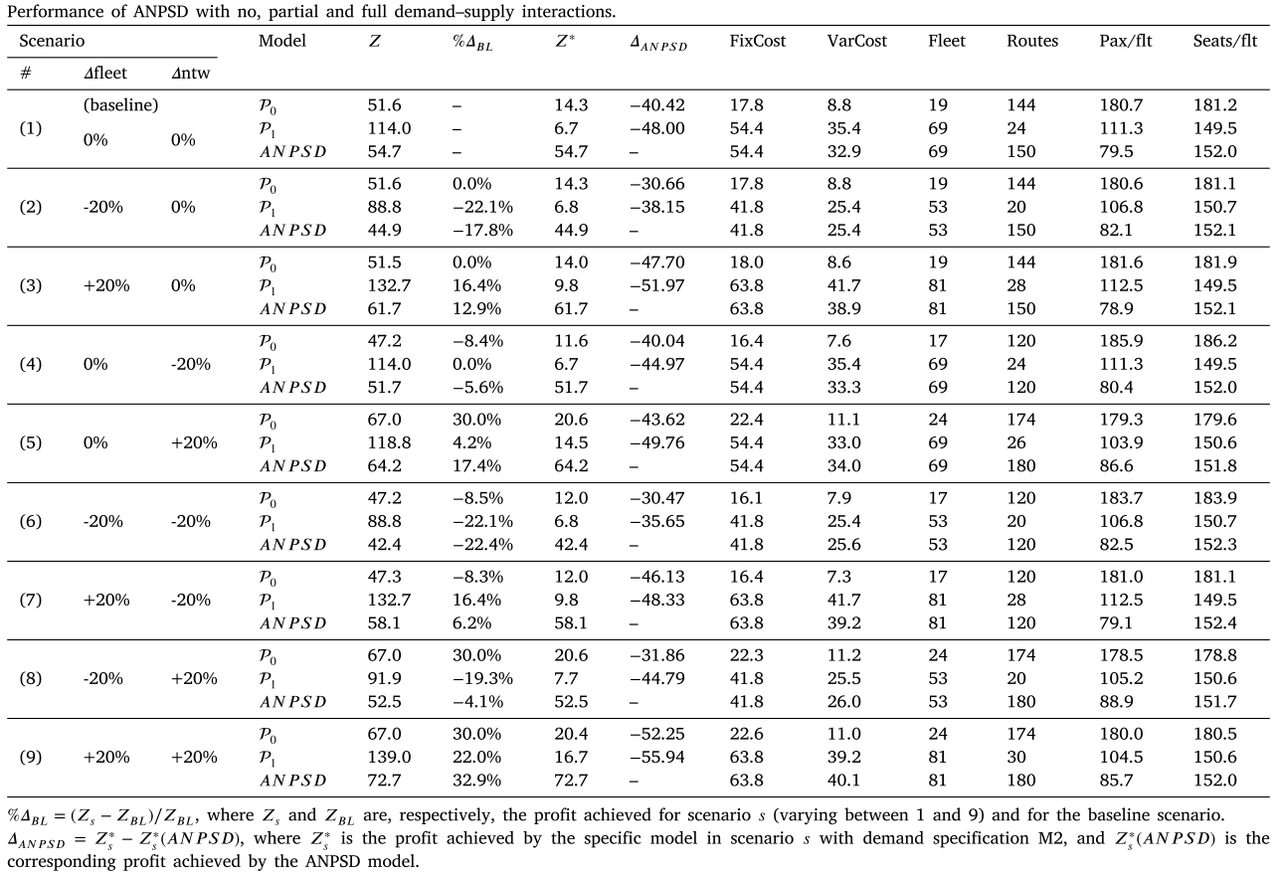
模型 P 0 \mathcal{P}_0 P0与 ANPSD 模型相比优先考虑具有少量航班的最大机型。 P 0 \mathcal{P}_0 P0完全从供应方角度出发,尽可能经济高效地匹配需求。 因此,机队规模变化不会影响估计利润但网络扩张和收缩对 P 0 \mathcal{P}_0 P0方案有重大影响。模型 P 1 \mathcal{P}_1 P1最大限度地提高了贡献利润率最高的路线上的飞机服务频率,网络收缩不会影响 P 1 \mathcal{P}_1 P1的估计利润,网络扩展带来的收益很小,但机队变化对 P 1 \mathcal{P}_1 P1方案有非常显著的影响。ANPSD 通过平衡机队和网络考虑因素,采取了折中方案。当网络固定时,机队收缩会使利润减少,而机队扩张会使利润增加,这表明当前的网络尚未饱和,通过增加现有路线的容量会产生潜在的好处。当机队固定时,网络收缩导致利润减少,因为可以重新部署从取消的航线中恢复的机队运力,以加强最有利可图的航线的供应。 在网络收缩,机队扩张的情景中,该模型建议放弃以激烈竞争和较低价格为特征的航线,更加集中在主要枢纽的运营上,从而形成枢纽整合战略。在机队收缩、网络扩张的情景中,该模型建议开辟通往意大利航空公司目前未提供服务的重要地点的新航线。
5. 总结与展望
本文开发了一种新型的建模和算法框架来优化航空网络,该模型与忽略供需相互作用的方法相比,更能够捕捉服务频率、网络结构和乘客需求之间的相互作用。因为该模型强调了不同网络规划优化决策、航线选择、飞行频率和机队组成的重要性,所以其可以作为提供有效决策的工具来支持航空公司的战略规划。未来在航线网络规划方面的研究可以在更细分的市场层面上开发数据驱动的乘客需求估计模型,并改善对竞争和不确定性的处理,以便在网络规划阶段更好地评估竞争航空公司之间的市场动态,系统地整合需求和供应之间的相互依存关系。
参考文献:
[1] S. Birolini, A. Jacquillat, M. Cattaneo, and A. P. Antunes, “Airline network planning: Mixed-integer non-convex optimization with demand–supply interactions,” Transportation Research Part B: Methodological, vol. 154, pp. 100–124, 2021.