插入排序

把当前遍历到的元素前的元素序列是排好序的,把当前元素放到前边的序列中进行排序。

直接插入排序

不带哨兵

void InsertSort(int A[],int n)
{
int i,j,temp;
for(i=1;i<n;i++)
if(A[i]<A[i-1])
{
temp=A[i];
for(j=i-1;j>=0 && A[j]>temp;--j)
A[j+1]=A[j];
A[j+1]=temp;
}
}

带哨兵

在这里插入图片描述
数组第一个元素为哨兵，记录当前要排序的元素，也充当了temp的作用

折半插入排序

在这里插入图片描述
有个疑问，带哨兵变量的直接插入排序循环中，为什么不需要判断j>0

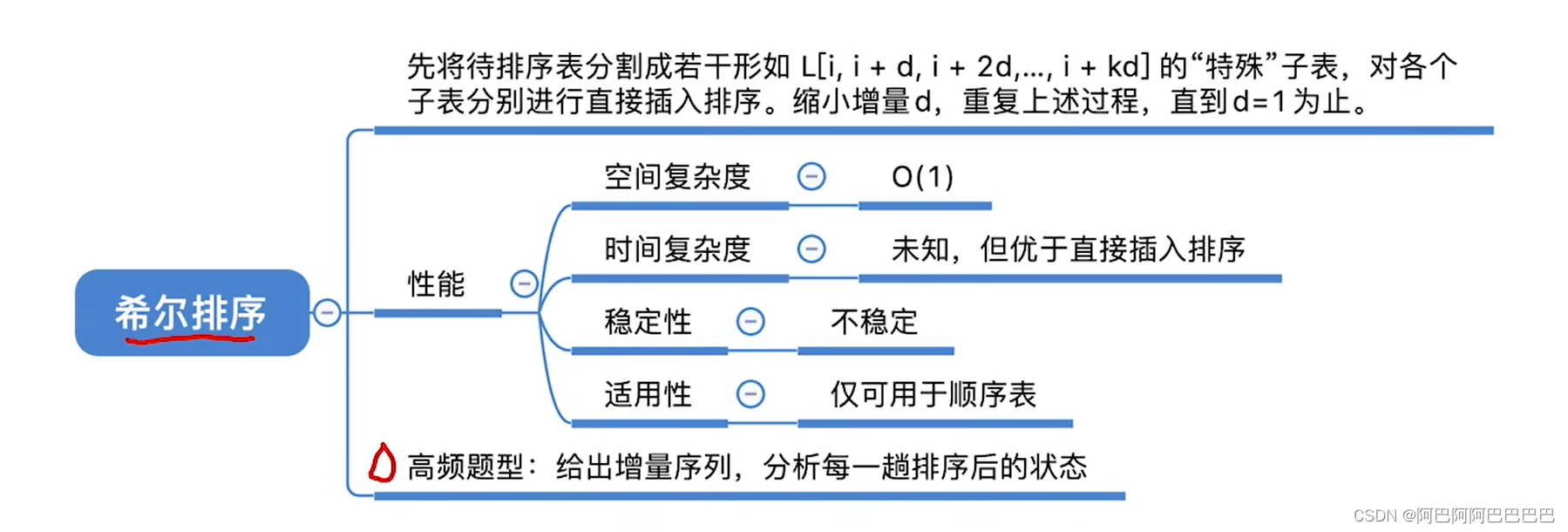
希尔排序

在这里插入图片描述

for(i=d+1;i<=n,++i)第一趟遍历，指向第一个子表中的第二个元素A[d+1]
按照直接插入排序的规则，比较当前指向的元素和其前面一个元素之间的大小关系if(A[i] < A[i-d])
判断子表元素是否有序,如果有序就直接开始下一轮循环i++
如果不是有序的，则使用带哨兵的直接插入排序的方法，进行排序

交换排序

冒泡排序

第一趟排序使关键字最小的一个元素排到最前面，王道视频中是从后向前遍历的，并且保持的是升序序列。
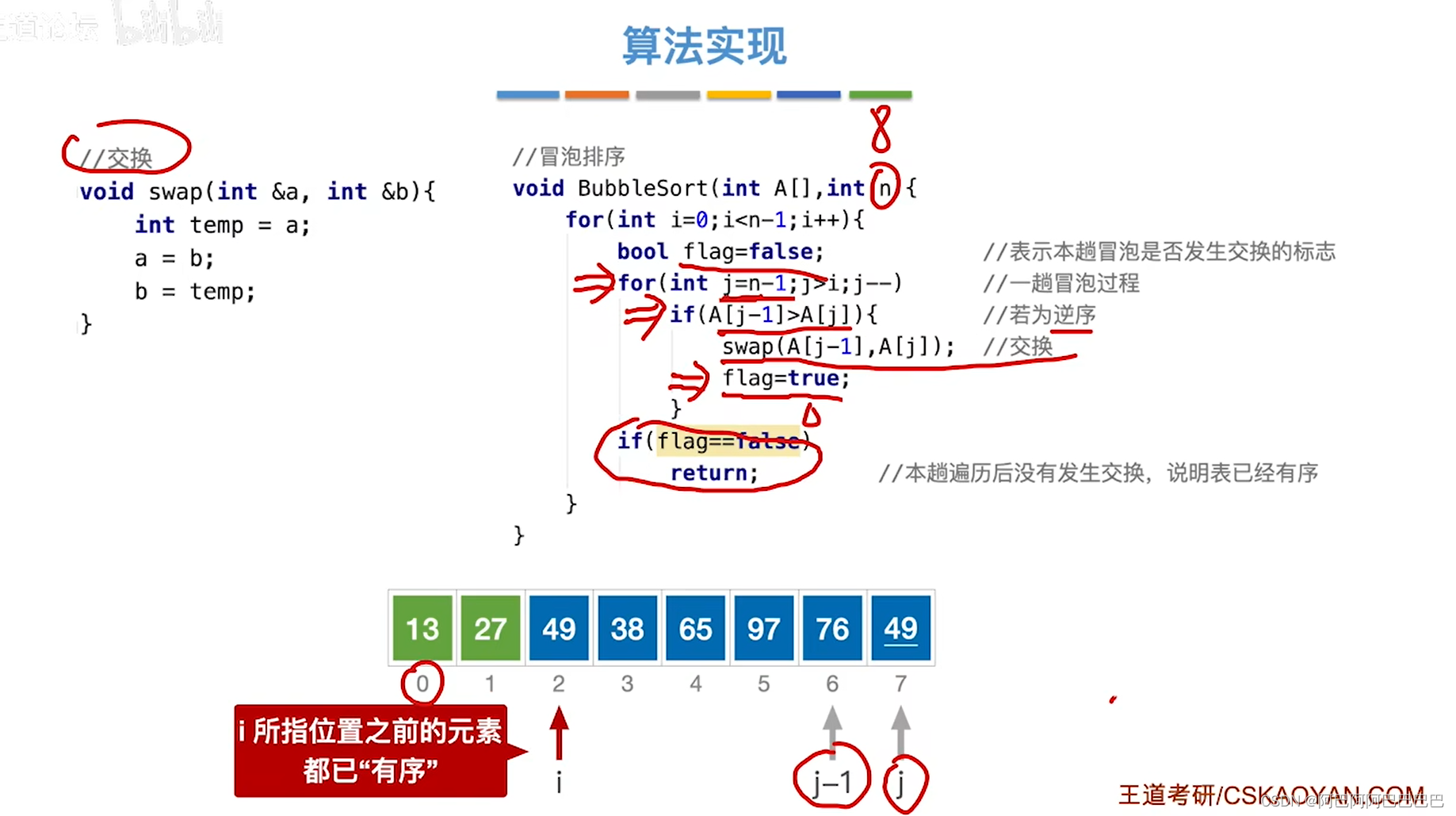在这里插入图片描述只有A[j-1]>A[j]时才会交换，保证了算法的稳定性。

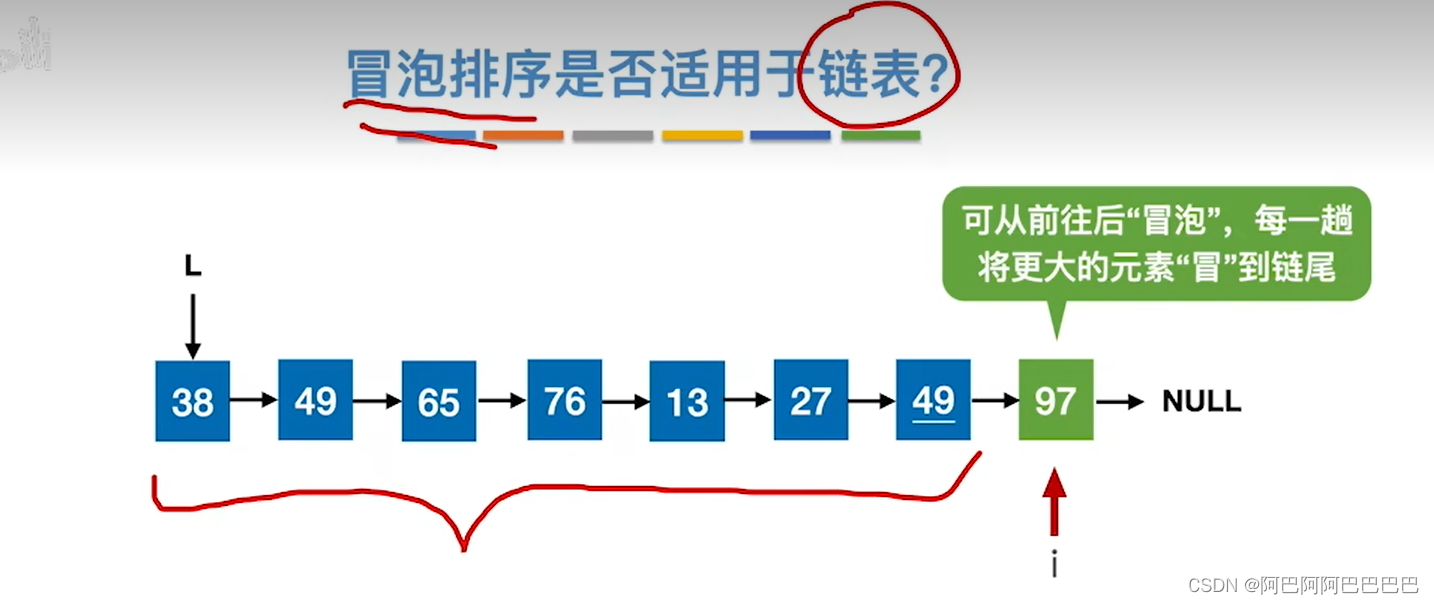
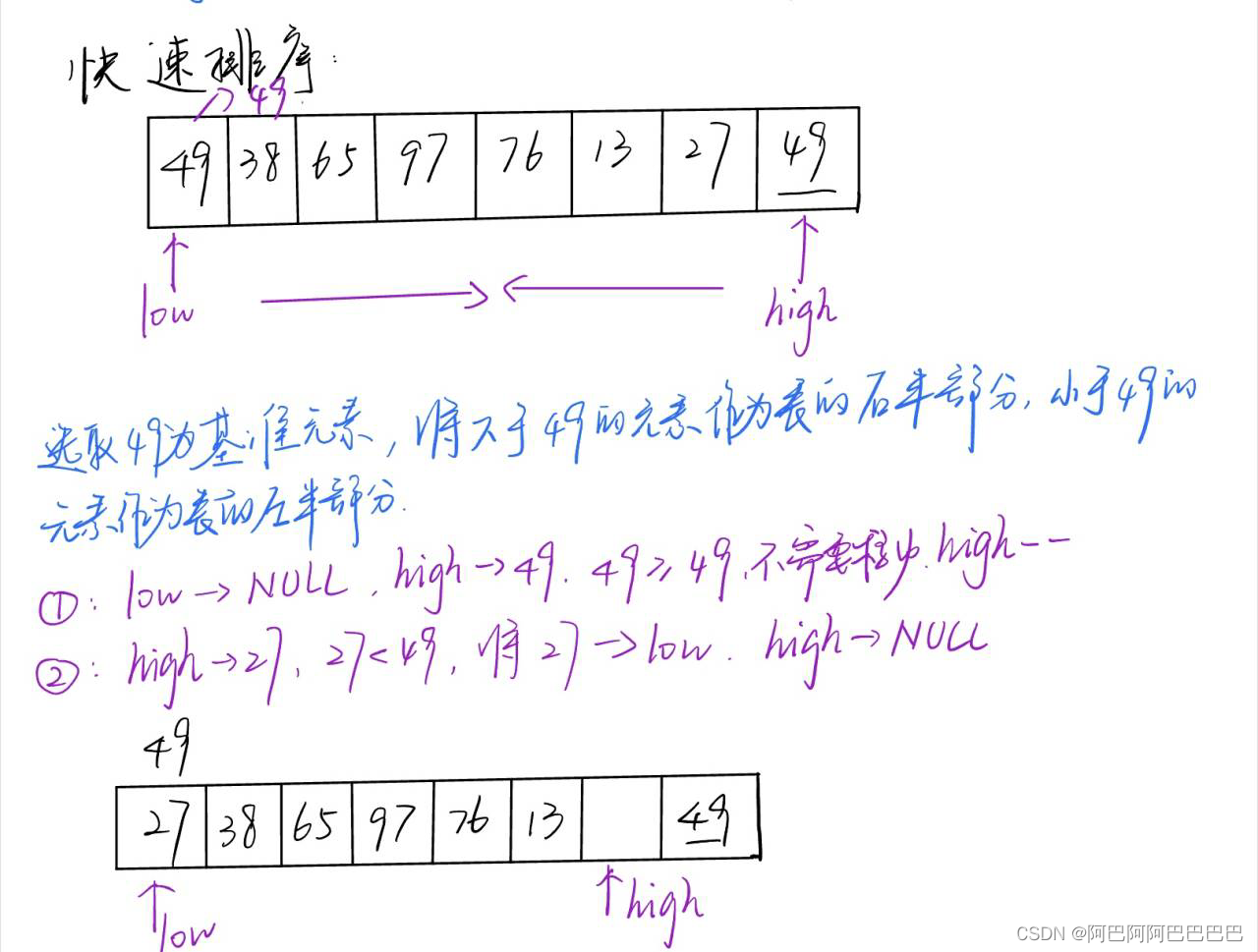
快速排序

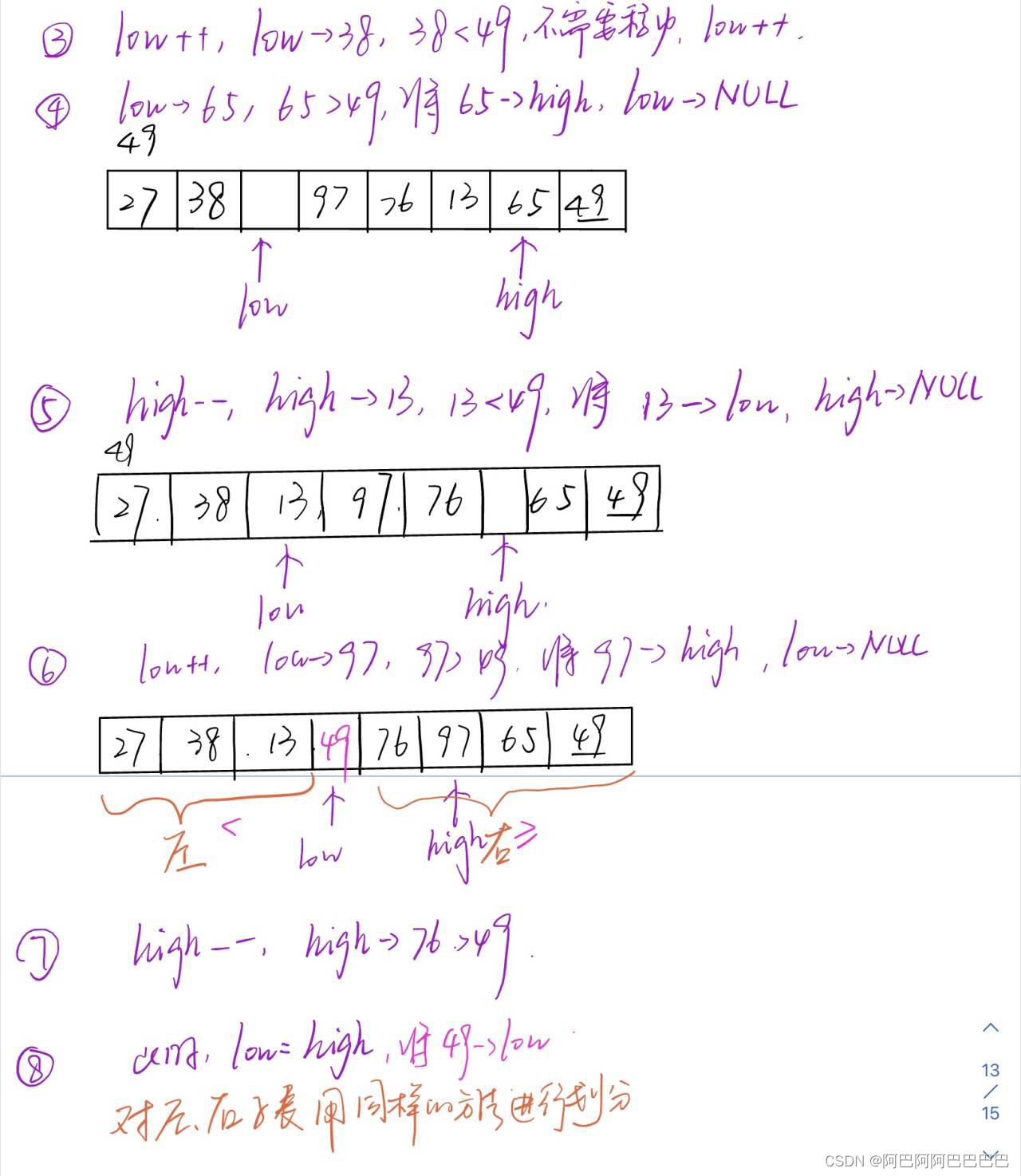
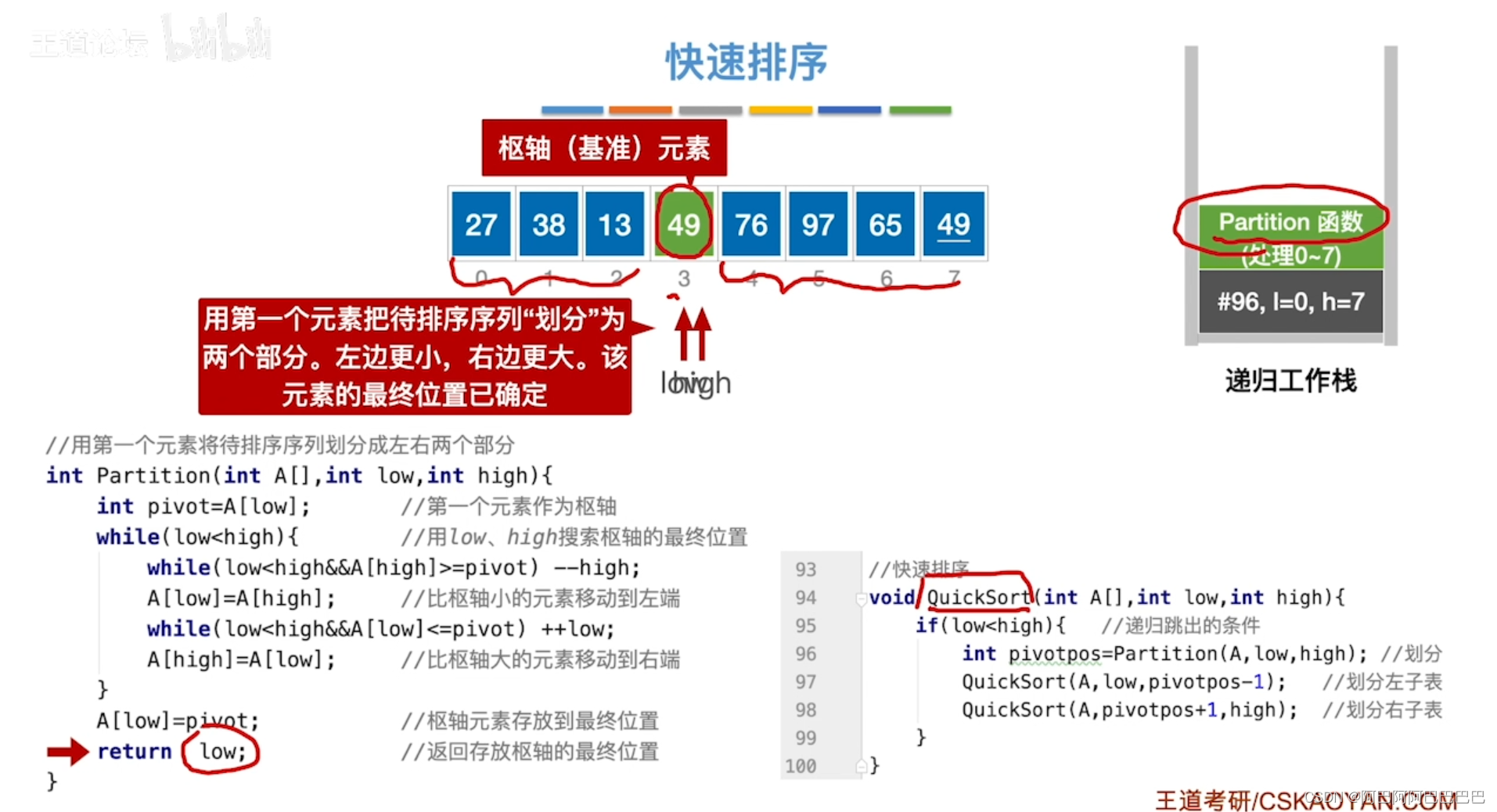
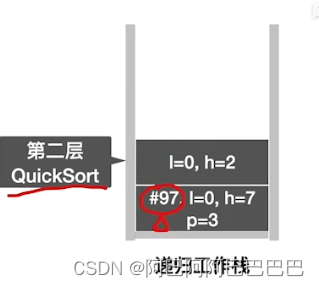
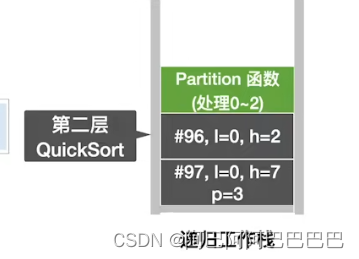
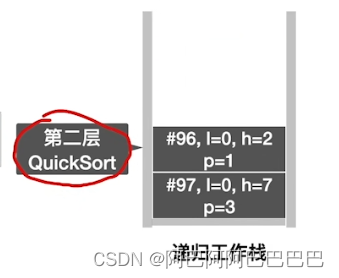
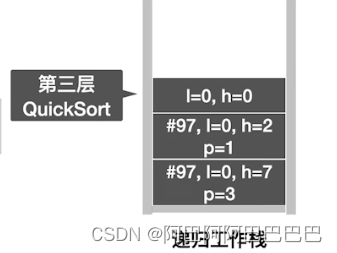
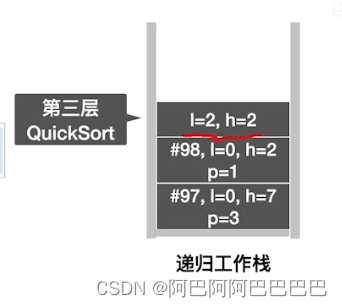
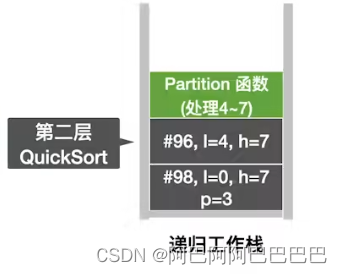
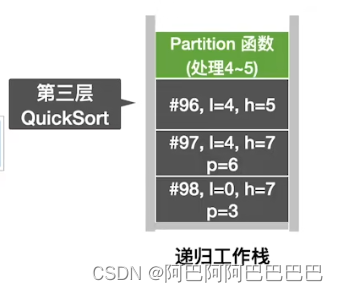
在这里插入图片描述

选择题整理总结

1.在排序过程中，每趟都能确定一个元素在其最终位置有冒泡排序、简单选择排序、堆排序、快速排序，前三者能形成全局有序的子序列，后者能确定枢轴元素的最终位置。
2.基于插入、交换、选择的三种排序方法中，通常简单方法是稳定的，但是简单选择排序是例外，复杂的方法都是不稳定的。
3.插入排序的核心：将待插入元素插入前面的有序字表

确定的当前记录在前面有序子表中的位置，直接插入排序采用顺序查找法
折半插入排序采用折半查找法

排序的趟数：n-1
元素的移动次数取决于初始序列，两者相同
使用的辅助空间数量O(1)
折半插入排序的比较次数和初始序列无关，为O(nlogn)
直接插入排序的比较次数和初始序列有关，为O(n)~O(n^2)

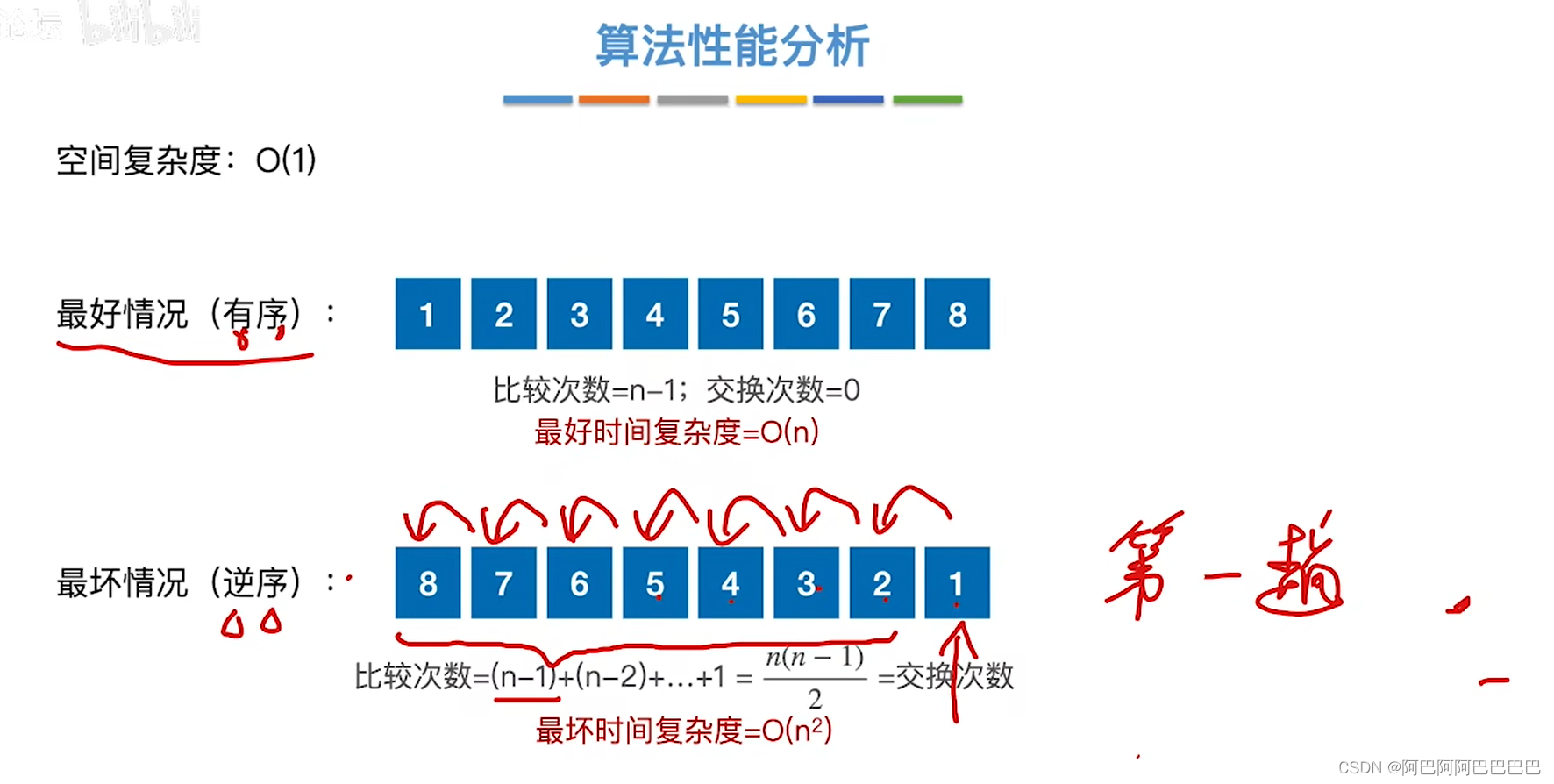
4.对于n个不同元素利用冒泡法从小到大排序，在从大到小情况下元素交换次数最多
对于一个逆序的序列进行冒泡排序，需要进行比较n(n-1)/2次
5.（D）

看条件想到基数排序，假设对一些两位数排序，个位是k1，十位是k2，则不符合基数排序。基数排序，先排个位时，是小的在后
所以应该是个位是k2，十位是k1，先k2再k1，对k1应该使用稳定的排序算法。k1直接插入排序是稳定的，选D
6.（C）（C）

7.选择排序在排序过程中比较次数与序列的初始状态无关，为 (n-1)n/2次
8.归并排序在一趟结束后不一定能选出一个元素放在其最终位置上
9.归并排序在排序过程中的比较次数的数量级与序列的初始状态无关
10.对N个元素进行k路归并排序，排序的趟数m=cell(logk(N))
11.很重要的表
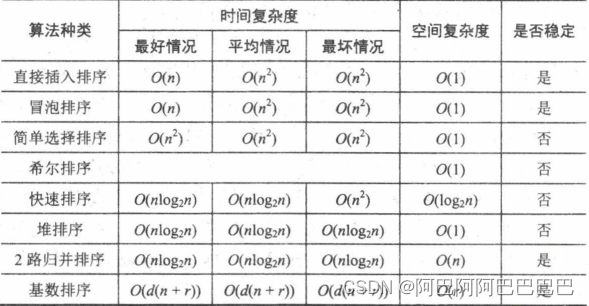
在这里插入图片描述