01背包：n种物品，每种物品只有1个，有相应的重量和价值

最多只能装m的重量，最多价值为多少？

dp[i][j] : [0, i]物品任取放进容量为j的背包里

不放物品i：dp[i-1][j]

放物品i：dp[i-1][j-weight[i]] + value[i]

        dp[i-1][j-weight[i] - 不放物品i的时候（容量腾出i），所放的最大价值

        value[i] - 把i物品放进去，最终最大价值

递推公式：放i和不放i两种情况

dp[i][j] = max( dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

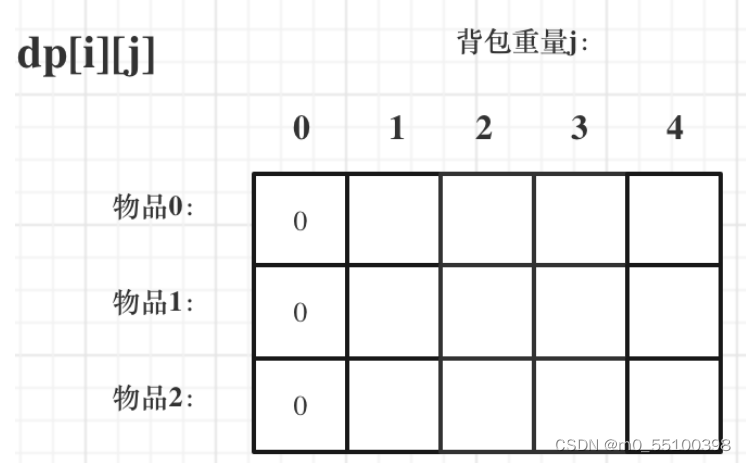
初始化：i是物品，j是重量，初始化第一行和第一列

根据递推公式：

        dp[i-1][j] - 上方

        dp[i-1][j-weight[i]] + value[i] - 左上方

第一列：容量是0，初始化成0

第一行：根据物品0来进行初始化

其他位置：任意值

 遍历：

先背包再物品都可以

DP41 【模板】01背包

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int bageweight = 0; // 背包重量
    int size = 0; // 物品数量
    cin >> size >> bageweight;

    vector<int> weight(size, 0);
    vector<int> value(size, 0);
    for(int i=0; i<size; ++i) {
        cin>>weight[i];
        cin>>value[i];
    }

    // 定义dp数组：表示 [0, i]物品任取，背包容量为j的最大价值
    vector<vector<int>> dp(size, vector<int>(bageweight+1, 0));
    // 初始化:第一行
    for(int i=weight[0]; i<=bageweight; ++i) {
        dp[0][i] = value[0];
    }

    // 先遍历物品 再遍历背包
    for(int i=1; i<size; ++i) {
        for(int j=0; j<=bageweight; ++j) {
            if(j<weight[i]) dp[i][j] = dp[i-1][j];
            // 动态规划函数
            else dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
        }
    }
    cout<<dp[size-1][bageweight];

}
// 64 位输出请用 printf("%lld")

一维dp数组

滚动数组：更新一行一行；上一层数据进行拷贝

dp[j] ：容量为j的背包，所背最大价值为dp[j]

递推公式：dp[j] = max(dp[j], dp[j-weight[i]]+value[i])

初始化：0

遍历顺序：

第一个遍历是物品（先行，一列一列遍历--拷贝）

第二个是背包（倒序）- 避免重复添加

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int bageweight = 0; // 背包重量
    int size = 0; // 物品数量
    cin >> size >> bageweight;

    vector<int> weight(size, 0);
    vector<int> value(size, 0);
    for(int i=0; i<size; ++i) {
        cin>>weight[i];
        cin>>value[i];
    }

    vector<int> dp(bageweight+1, 0);
    for(int i=0; i<size; ++i) {
        for(int j=bageweight; j>=weight[i]; --j) {
            dp[j] = max(dp[j], dp[j-weight[i]]+value[i]);
        }
    }

    cout<<dp[bageweight];

复习：

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int bageweight = 0; // 背包重量
    int size = 0; // 物品数量
    cin >> size >> bageweight;

    vector<int> weight(size, 0);
    vector<int> value(size, 0);
    for(int i=0; i<size; ++i) {
        cin>>weight[i];
        cin>>value[i];
    }

    // [0, i] 个物品 背包重量为j的情况下所能取到的最大价值
    vector<vector<int>> dp(size, vector(bageweight, 0));
    // 初始化
    // 第一行
    for(int j=weight[0]; j<=bageweight; ++j) {
        dp[0][j] = value[0];
    }
    for(int i=1; i<size; ++i) {
        for(int j=0; j<=bageweight; ++j) {
            if(j<weight[i]) dp[i][j] = dp[i-1][j];
            else dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
        }
    }

    cout<<dp[size-1][bageweight];
}

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int bageweight = 0; // 背包重量
    int size = 0; // 物品数量
    cin >> size >> bageweight;

    vector<int> weight(size, 0);
    vector<int> value(size, 0);
    for(int i=0; i<size; ++i) {
        cin>>weight[i];
        cin>>value[i];
    }

    vector<int> dp(bageweight+1, 0);

    for(int i=0; i<size; ++i) {
        for(int j=bageweight; j>=weight[i]; --j) {
            dp[j] = max(dp[j], dp[j-weight[i]]+value[i]);
        }
    }

    cout<<dp[bageweight];
}

416. 分割等和子集

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(int num:nums) {
            sum += num;
        }
        if(sum%2==1) {
            return false;
        }
        int target = sum/2;

        vector<int> dp(10001, 0);
        for(int i=0; i<nums.size(); ++i) {
            for(int j=target; j>=nums[i]; --j) {
                dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);
            }
        }
        if(dp[target]==target) return true;
        return false;
    }
};