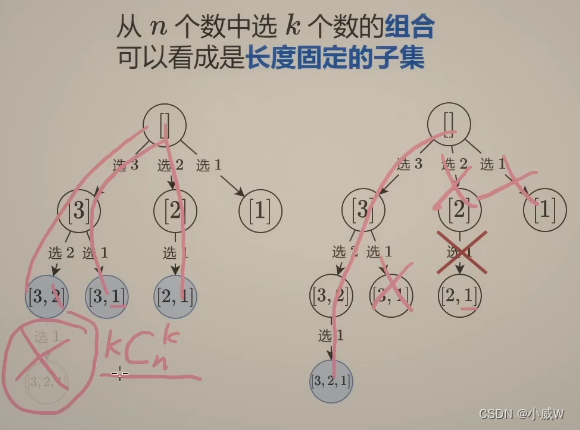
组合型回溯

组合型和子集型之间的差异在哪里呢？
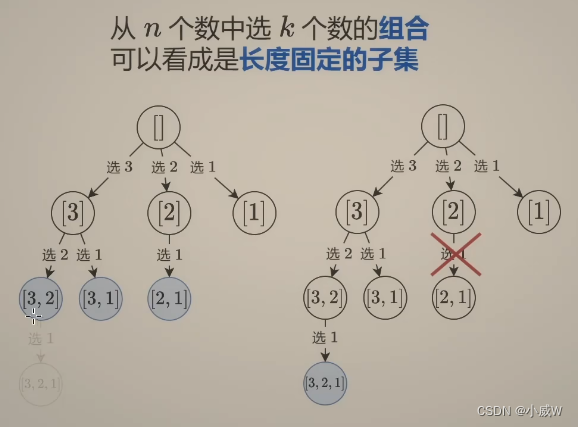
在这里插入图片描述

相比子集问题，组合问题是可以做一些额外的优化的（因为只需要得到某些特定的子集）。

同样是【选和不选】以及【枚举选哪个】这两种思路。
（具体用哪种思路根据题目特点来做，哪种更好些就选哪种写法）

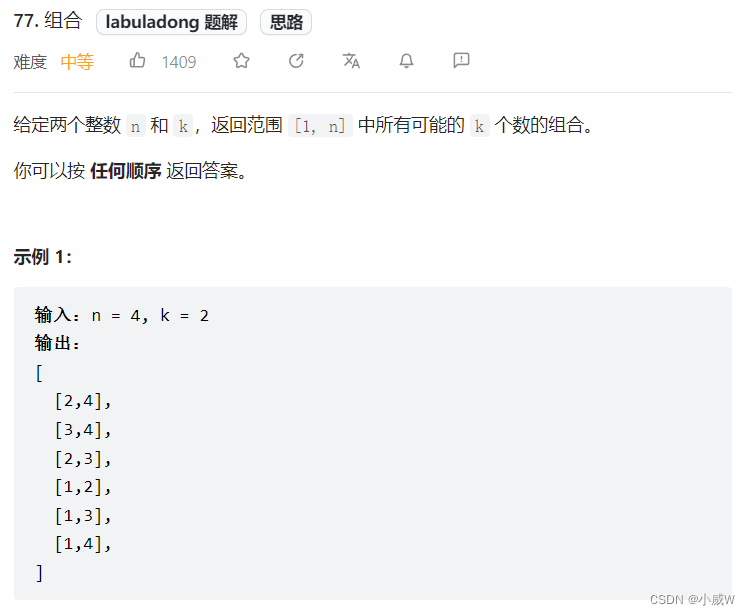
例题1——组合

https://leetcode.cn/problems/combinations/
在这里插入图片描述

从输入考虑模板

依然是考虑每个数字选或不选，与子集型回溯的差异在于，结果的元素数量必须是k。

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> combine(int n, int k) {
        dfs(1, n, k);
        return ans;
    }

    public void dfs(int i, int n, int k) {
        if (k == 0) {
            ans.add(new ArrayList(t));
            return;
        }
        if (i > n) return;
        dfs(i + 1, n, k);
        t.add(i);
        dfs(i + 1, n, k - 1);
        t.remove(t.size() - 1);
    }
}

从答案考虑模板

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> combine(int n, int k) {
        dfs(1, n, k);
        return ans;
    }

    public void dfs(int startIndex, int n, int k) {
        if (k == 0) {
            ans.add(new ArrayList(t));
            return;
        }
        for (int i = startIndex; i <= n; ++i) {
            t.add(i);
            dfs(i + 1, n, k - 1);
            t.remove(t.size() - 1);
        }
    }
}

例题2——括号生成

解法一

选左括号还是右括号

class Solution {
    List<String> ans = new ArrayList();
    StringBuilder t = new StringBuilder();

    public List<String> generateParenthesis(int n) {
        dfs(n, n);
        return ans;
    }

    public void dfs(int n1, int n2) {
        if (n1 == 0 && n2 == 0) {
            ans.add(t.toString());
            return;
        }
        if (n1 > 0) {   // 左括号
            t.append('(');
            dfs(n1 - 1, n2);
            t.deleteCharAt(t.length() - 1);
        }
        if (n2 > n1) {  // 右括号
            t.append(')');
            dfs(n1, n2 - 1);
            t.deleteCharAt(t.length() - 1);
        }
    }
}

其实回溯里的 if 就相当于是在做剪枝了，所谓的剪枝就是提前过滤掉不合理的答案。

解法二

枚举左括号出现的位置

class Solution {
    List<String> ans = new ArrayList();
    List<Integer> pos = new LinkedList();   // 存储左括号的位置

    public List<String> generateParenthesis(int n) {
        dfs(0, 0, n);
        return ans;
    }

    public void dfs(int startIndex, int cnt, int n) {
        if (cnt == n) {
            char[] chs = new char[2 * n];
            Arrays.fill(chs, ')');
            for (int idx: pos) chs[idx] = '(';
            ans.add(new String(chs));
            return;
        }
        for (int i = startIndex; i <= 2 * cnt; ++i) {
            pos.add(i);
            dfs(i + 1, cnt + 1, n);
            pos.remove(pos.size() - 1);
        }
    }
}

这里 for 循环中的 i <= 2 * cnt 相当于剪枝。

剪枝

这里以解法一为例介绍剪枝操作。
由于答案中必须有 k 个元素，因此如果选到 i 的时候，还有 n - i + 1 个元素可供选择，因此如果可供选择的数字已经少于还需要选择的元素，那么就可以不再继续往下尝试了。

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> combine(int n, int k) {
        dfs(1, n, k);
        return ans;
    }

    public void dfs(int i, int n, int k) {
        if (n - i + 1 < k) return;	// 剪枝
        if (k == 0) {
            ans.add(new ArrayList(t));
            return;
        }
        dfs(i + 1, n, k);
        t.add(i);
        dfs(i + 1, n, k - 1);
        t.remove(t.size() - 1);
    }
}

对于模板二的剪枝方式为：

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> combine(int n, int k) {
        dfs(1, n, k);
        return ans;
    }

    public void dfs(int startIndex, int n, int k) {
        if (k == 0) {
            ans.add(new ArrayList(t));
            return;
        }
        for (int i = startIndex; i <= n - k + 1; ++i) {		// 剪枝 i <= n - k + 1
            t.add(i);
            dfs(i + 1, n, k - 1);
            t.remove(t.size() - 1);
        }
    }
}