【备战秋招】每日一题:2023.04.26-华为OD机式-第三题-MC方块

在线评测链接:P1231

题目内容

MC最新版本更新了一种特殊的方块，幽匿催发体。这种方块能够吸收生物死亡掉落的经验并感染周围方块，使其变成幽匿块。Steve想要以此为基础尝试搭建一个经验仓库，他来到了创造超平坦模式，在只有草方块组成的平坦世界上进行他的实验。

在Steve的实验中，幽匿催发体可以看做每次吸收经验后会向自己平面方向上的周围八个方块进行感染，使其变成幽匿催发体。Steve任意选择了 n 个坐标点作为幽匿催发体的起始方块，接下来每天都会给予这些催发体足够使自身范围向外扩展一圈的经验。当有两个或以上的幽匿催发体的感染范围重叠时，重叠区域的方块会吸收更多的经验，吸收经验的数量为该方块所在不同幽匿催发体感染范围数量的整数倍。

如下方三张图所示，蓝色点A、B为初始幽匿催发体的位置

![img-vsSiykEJ-1687420811924)(/hw/P1231/1.png)]

第二天，向周围扩散感染

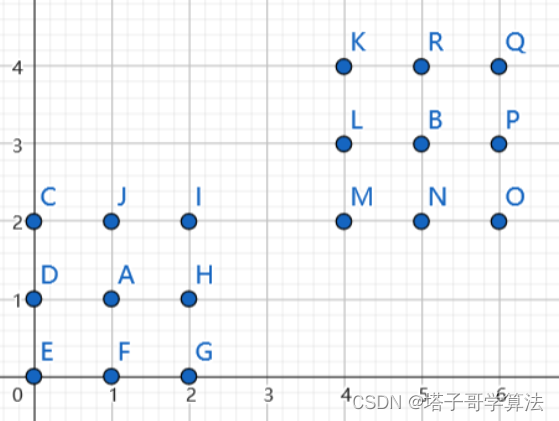
在这里插入图片描述

第三天，两个催发体的感染范围出现重叠，重叠部分的经验倍数 M 为2，其余则为1，以此类推。

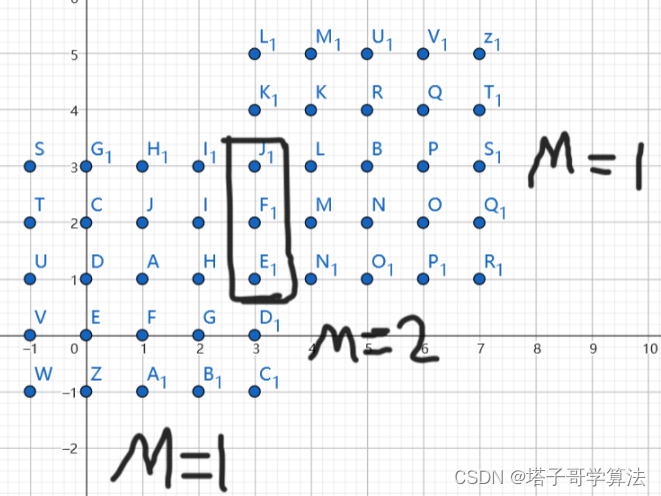
Steve想要知道多少天以后，会出现至少有一个方块的经验存储量的倍数可以达到给定的 M ？

输入描述

第一行输入整数 M。(2c= M <= n)

第二行输入幽匿催发体个数 n。 (2<= n <= 50)

后面连续 n 行输入第 i 个幽匿催发体 i 的初始位置 [xi, yi]。 (1<= xi，yi<= 10^9)

输出描述

输出找到一个方块至少同时处在 M 个幽匿催发体的感染范围的最少天数，找不到返回 0

样例

样例1

输入

输出

说明

说明: 在第2天，点(4.0)、(4.1)、 (4.2)与(4,3)将同时处在两个幽匿催发体发感染范围，如图红色点所示。

样例2

输入

输出

思路：二分答案+二维差分

二分答案

刷过一定量的二分答案题，我们就很容易发现这个题要求的答案<至少有一个方块的经验存储量的倍数可以达到给定的 M的天数>有单调性，即:

1.天数越久，就会有越多点重合。就越可能满足给定条件。

2.无限久后，一定会有点达到 $M$ 的重复。

如何写check函数？

直接数组模拟显然不行，因为平面太大了，二维数组开不了这么大。但是我们这个平面上有非常多的点是无用的 。我们把关键点(每个矩阵的左上角，右下角)提出来进行离散化，在一个更小的平面内进行二维差分即可。

知识点学习

没接触过离散化+二维差分的估计会觉得有些抽象，一些学习资料

1.一维差分:前缀和&差分 Oi-Wiki

2.二维差分:二维差分知乎

3.二维坐标离散化:二维坐标离散化

tips:这是一道力扣杯的原题。见LCP 74.最强祝福力场 -灵神题解

类似题目推荐

一道比较有难度的二分答案题。要吃透这类题，需要多加练习！

初识二分答案

1.LeetCode 875. 爱吃香蕉的珂珂

2.LeetCode 2187. 完成旅途的最少时间

3.LeetCode 6325. 修车的最少时间

4.LeetCode 2226. 每个小孩最多能分到多少糖果

真题

P1236 美团实习-2023.04.15-第二题-分糖果

P1189. 华为实习 2023.04.12-实习笔试-第一题-购物系统的降级策略

P1006. 华为秋招 2022.9.21-数组取min

P1106. 腾讯音乐 2023.3.23-第二题-划分字符串

进阶练习

P1093. 米哈游 2023.03.19-第三题-塔子哥的无限字符串 - 二分答案 + 细节讨论

P1169 2023.04.08-美团春招-第四题-田地行走 - 二分答案 + 多源BFS

P1102 阿里巴巴 2023.03.21-第三题-数数 - 二分答案 + 数位dp

代码

C++

#include<bits/stdc++.h>
using namespace std;
const int N=55;
typedef pair<int,int>PII;
#define x first
#define y second
vector<PII> w;
int n,m;
int check(vector<PII>& ps,int mid) 
{
        // 1. 统计所有左下和右上坐标
        vector<long long> xs, ys;
        for (auto &p: ps) {
            auto i = p.x;
            auto j = p.y;
            xs.push_back(i - mid );
            xs.push_back(i + mid);
            ys.push_back(j - mid );
            ys.push_back(j + mid);
        }

        // 2. 排序去重
        sort(xs.begin(), xs.end());
        xs.erase(unique(xs.begin(), xs.end()), xs.end());
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        // 3. 二维差分
        int n = xs.size(), m = ys.size(), diff[n + 2][m + 2];
        memset(diff, 0, sizeof(diff));
        for (auto &p: ps) {
            auto i = p.x;
            auto j = p.y;
            int r1 = lower_bound(xs.begin(), xs.end(), i - mid ) - xs.begin();
            int r2 = lower_bound(xs.begin(), xs.end(), i + mid) - xs.begin();
            int c1 = lower_bound(ys.begin(), ys.end(), j - mid ) - ys.begin();
            int c2 = lower_bound(ys.begin(), ys.end(), j + mid) - ys.begin();
            // 将区域 r1<=r<=r2 && c1<=c<=c2 上的数都加上 x
            // 多 +1 是为了方便求后面复原
            ++diff[r1 + 1][c1 + 1];
            --diff[r1 + 1][c2 + 2];
            --diff[r2 + 2][c1 + 1];
            ++diff[r2 + 2][c2 + 2];
        }

        // 4. 直接在 diff 上复原，计算最大值
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
                ans = max(ans, diff[i][j]);
            }
        }
        return ans;
 }
int main()
{
    cin>>m>>n;
    for(int i=0;i<n;i++)
    {
        int x,y;
        cin >> x >> y;
        w.push_back({x,y});
    }
    int l = 0,r = 1e9;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(check(w,mid) >= m){
            r=mid;
        }
        else l = mid + 1;
    }
cout << l << endl;
return 0;
}
// by yhy

python

M = int(input())
n = int(input())
c = []
for i in range(n):
    x, y = map(int, input().split())
    c.append((x, y))

def check(day):
    xs = set()
    ys = set()
    # 1. 统计所有左下和右上坐标
    for x, y in c:
        xs.add(x-day)
        xs.add(x+day)
        ys.add(y-day)
        ys.add(y+day)
    # 2. 排序去重
    xs = sorted(xs)
    ys = sorted(ys)
    xs_idx = {x:i+1 for i, x in enumerate(xs)}
    ys_idx = {x:i+1 for i, x in enumerate(ys)}
    
    # 二维差分
    diff = [[0] * (len(ys)+2) for _ in range(len(xs)+2)]
    for x, y in c:
        # 将区域 r1<=r<=r2 && c1<=c<=c2 上的数都加上 x
        # 多 +1 是为了方便求后面复原
        x_idx = xs_idx[x-day]
        x_idx_ = xs_idx[x+day]+1
        y_idx = ys_idx[y-day]
        y_idx_ = ys_idx[y+day]+1
        diff[x_idx][y_idx] += 1
        diff[x_idx_][y_idx] -= 1
        diff[x_idx][y_idx_] -= 1
        diff[x_idx_][y_idx_] += 1
    ans = 0
    #  4.直接在 diff 上复原，计算最大值
    for i in range(1, len(xs)+1):
        for j in range(1, len(ys)+1):
            diff[i][j] += diff[i-1][j] + diff[i][j-1] - diff[i-1][j-1]
            ans = max(ans, diff[i][j])
    return ans

max_x = max(c)[0]
min_x = min(c)[0]
max_y = max(c, key=lambda x: x[1])[1]
min_y = min(c, key=lambda x: x[1])[1]


l = 0
r = max(max_x-min_x, max_y-min_y) // 2 + 2

while l < r:
    mid = (l+r) // 2
    tmp = check(mid)
    if tmp == M:
        r = mid
    elif tmp < M:
        l = mid+1
        
    else:
        r = mid
print(r)
# by mathcoder2

Java

超时

import java.util.*;

public class Main {
    // LCP 74. 最强祝福力场
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int m = scan.nextInt(), n = scan.nextInt();
        int[][] points = new int[n][2];
        for (int i = 0; i < n; i++) {
            points[i] = new int[]{scan.nextInt(), scan.nextInt()};
        }
        int l = 0, r = (int) 1e9 + 5, ans = -1;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(points, mid, m)) ans = r = mid;
            else l = mid + 1;
        }
        System.out.println(ans == -1 ? 0 : ans);
    }

    public static boolean check(int[][] points, int mid, int m) {
        int n = points.length;
        List<int[]> overlaps = new ArrayList<>();
        // 最大强度必是每个正方形的交点
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (Math.max(Math.abs(points[i][0] - points[j][0]), Math.abs(points[i][1] - points[j][1])) > 2 * mid) continue;
                // 点i左上角坐标
                int lx1 = points[i][0] - mid, ly1 = points[i][1] - mid;
                // 点i右下角坐标
                int rx1 = points[i][0] + mid, ry1 = points[i][1] + mid;
                // 点j左上角坐标
                int lx2 = points[j][0] - mid, ly2 = points[j][1] - mid;
                // 点j右下角坐标
                int rx2 = points[j][0] + mid, ry2 = points[j][1] + mid;
                // 重叠部分左上角坐标
                int ox1 = Math.max(lx1, lx2), oy1 = Math.max(ly1, ly2);
                // 重叠部分右下角坐标
                int ox2 = Math.min(rx1, rx2), oy2 = Math.min(ry1, ry2);
                overlaps.add(new int[]{ox1, oy1});
                overlaps.add(new int[]{ox1, oy2});
                overlaps.add(new int[]{ox2, oy1});
                overlaps.add(new int[]{ox2, oy2});
            }
        }
        for (int[] overlap : overlaps) {
            int cnt = 0;
            for (int[] point : points) {
                if (Math.max(Math.abs(overlap[0] - point[0]), Math.abs(overlap[1] - point[1])) <= mid) cnt++;
            }
            if (cnt >= m) return true;
        }
        return false;
    }
}

Go

package main

import (
	"fmt"
)

var M, n int
var goast [][]int

type point struct {
	x, y int
}

func main() {
	fmt.Scan(&M, &n)
	var x, y int
	for i := 0; i < n; i++ {
		fmt.Scan(&x, &y)
		goast = append(goast, []int{x, y})
	}
	// 二分答案
	l := 0
	r := int(1e9)
	res := -1
	for l < r {
		mid := (l + r) / 2
		if check(mid) {
			res = mid
			r = mid
		} else {
			l = mid + 1
		}
	}
	if res == -1 {
		fmt.Println(0)
	} else {
		fmt.Println(res)
	}

}

func check(mid int) bool {
	overlap := map[int]point{}
	for i := 0; i < n; i++ {
		for j := i + 1; j < n; j++ {
			if max(abs(goast[i][0]-goast[j][0]), abs(goast[i][1]-goast[j][1])) > 2*mid {
				continue
			}
			smallxi := goast[i][0] - mid
			bigxi := goast[i][0] + mid
			smallyi := goast[i][1] - mid
			bigyi := goast[i][1] + mid
			smallxj := goast[j][0] - mid
			bigxj := goast[j][0] + mid
			smallyj := goast[j][1] - mid
			bigyj := goast[j][1] + mid
			smallx := max(smallxi, smallxj)
			bigx := min(bigxi, bigxj)
			smally := max(smallyi, smallyj)
			bigy := min(bigyi, bigyj)
			var node point
			node.x, node.y = smallx, smally
			overlap[smallx*10+smally] = node
			node.x, node.y = smallx, bigy
			overlap[smallx*10+bigy] = node
			node.x, node.y = bigx, smally
			overlap[bigx*10+smally] = node
			node.x, node.y = bigx, bigy
			overlap[bigx*10+bigy] = node
		}
	}
    
	for _, node := range overlap {
		mcnt := 0
		x := node.x
		y := node.y
		for i := 0; i < n; i++ {
			if max(abs(x-goast[i][0]), abs(y-goast[i][1])) <= mid {
				mcnt += 1
				if mcnt >= M {
					return true
				}
			}
		}
	}
	return false
}

func max(x, y int) int {
	if x > y {
		return x
	}
	return y
}

func min(x, y int) int {
	if x < y {
		return x
	}
	return y
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

Js

let w = [];

function check(ps, mid) {
  // 1. 统计所有左下和右上坐标
  let xs = [], ys = [];
  for (let i = 0; i < ps.length; i++) {
    let p = ps[i];
    let j = p[0], k = p[1];
    xs.push(j - mid);
    xs.push(j + mid);
    ys.push(k - mid);
    ys.push(k + mid);
  }

  // 2. 排序去重
  xs = [...new Set(xs)].sort((a, b) => a - b);
  ys = [...new Set(ys)].sort((a, b) => a - b);

  // 3. 二维差分
  let n = xs.length, m = ys.length;
  let diff = Array.from(Array(n + 2), () => new Array(m + 2).fill(0));
  for (let i = 0; i < ps.length; i++) {
    let p = ps[i];
    let j = p[0], k = p[1];
    let r1 = binarySearch(xs, j - mid);
    let r2 = binarySearch(xs, j + mid);
    let c1 = binarySearch(ys, k - mid);
    let c2 = binarySearch(ys, k + mid);
    // 将区域 r1<=r<=r2 && c1<=c<=c2 上的数都加上 x
    // 多 +1 是为了方便求后面复原
    diff[r1 + 1][c1 + 1]++;
    diff[r1 + 1][c2 + 2]--;
    diff[r2 + 2][c1 + 1]--;
    diff[r2 + 2][c2 + 2]++;
  }

  // 4. 直接在 diff 上复原，计算最大值
  let ans = 0;
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= m; j++) {
      diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
      ans = Math.max(ans, diff[i][j]);
    }
  }
  return ans;
}

function binarySearch(arr, target) {
  let l = 0, r = arr.length - 1;
  while (l < r) {
    let mid = Math.floor((l + r) / 2);
    if (arr[mid] >= target) {
      r = mid;
    } else {
      l = mid + 1;
    }
  }
  return l;
}

process.stdin.resume();
process.stdin.setEncoding('utf-8');
let input = '';
process.stdin.on('data', (data) => {
    input += data;
    return;
});
process.stdin.on('end', () => {
    const lines = input.trim().split('\n');
    // write your code here
    let m = Number(lines[0].trim().split(' '));
    let n = Number(lines[1].trim().split(' '));
    for (let i = 0; i < n; i++) {
        let [x, y] = lines[i + 2].trim().split(' ').map(Number);
        w.push([x, y]);
    }
    let l = 0, r = 1e9;
    while (l < r) {
        let mid = Math.floor((l + r) / 2);
        if (check(w, mid) >= m) {
        r = mid;
        } else {
        l = mid + 1;
        }
    }
    console.log(l);
});