KMP

问题

字符串匹配问题，问字符串 str1中是否存在连续的子串与字符串str2相等,存在返回子串的起始位置，否则返回-1

思路

传统做法是依次遍历str1中的每个字符作为起始位置，看是否能凑出字符串str2.

KMP算法就是对传统做法的一种加速，对于有些节点是可以跳过的

数据

数组next ： 用于存储下标i前面长度为i-1的字符串 前缀 和 后缀相等的最长长度

实现

int f1(string str1,string str2)
{
    if(str1.size() < str2.size()) return 0;
    
    vector<int> arr = GetNextArr(str2);
    int i1 = 0 , i2 = 0;
    while(i1 < str1.size())
    {
        if(str1[i1] == str2[i2])
        {
            i1++;
            i2++;
        }
        else if(next[i2] == -1)
        {
            i1++;
        }
        else
        {
            i2 = next[i2];
        }
    }
    return i2 == str2.size() ? i1 - i2 : -1;
}
​
vector<int> GetNextArr(string str)
{
    if(str2.size() == 1)
    {
        return vector<int>(1,-1);
    }
    
    vector<int> next(str.size());
    next[0] = -1;
    next[1] = 0;
    int cn = 0;
    int i = 2;
    while(i < str.size())
    {
        if(next[cn] == str[i - 1])
        {
            next[i++] = ++cn;
        }
        else if(cn > 0)
        {
            cn = next[cn];
        }
        else
        {
            next[i++] = 0;
        }
    }
    return next;
}

思考

如何做到加速

 当i1位置字符和i2位置字符不相等时，i2来到前 i2 - 1 的 前缀和后缀相等的最长长度的下一个位置也就是next[i2].

因为i1前的字符和i2前的字符相等，可得到如图的切割，比较i1和k的字符，相当于str1的比较起始位置来到切割位置

为何可以跳过切割位置前面的字符

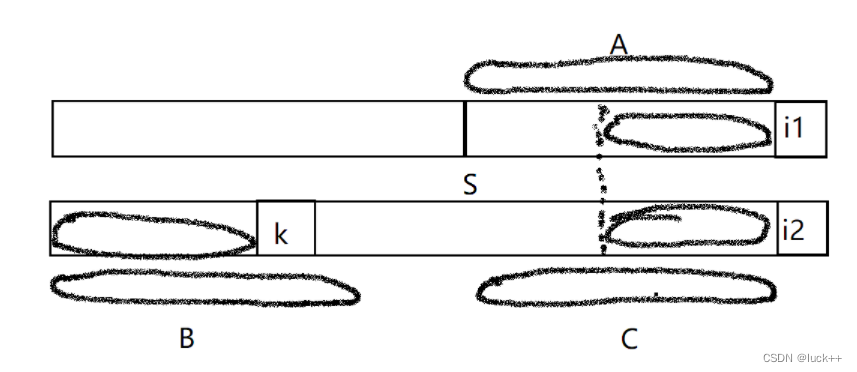
 假设S位置起始可以凑出字符串str2，那S到i1-1的长度A应与str2中的长度B中的字符相等。

由于i1前的字符和i2前的字符相等，则相等长度C和A中的字符应该相等，=》A=B=C 。

B=C，得到新的前缀和后缀相等的最长长度，违背了我们之前算出的结果，所以S起始不成立