【FPGA】Verilog：时序电路设计 | 自循环移位寄存器 | 环形计数 | 扭环计数

【FPGA】Verilog：时序电路设计 | 自循环移位寄存器 | 环形计数 | 扭环计数 | 约翰逊计数器

news2024/11/17 5:43:51

前言：本章内容主要是演示Vivado下利用Verilog语言进行电路设计、仿真、综合和下载

示例：计数器

功能特性：采用 Xilinx Artix-7 XC7A35T芯片
配置方式：USB-JTAG/SPI Flash
高达100MHz 的内部时钟速度
存储器：2Mbit SRAM N25Q064A SPI Flash（样图旧款为N25Q032A）
通用IO：Switch ：x8LED：x16Button：x5DIP：x8 通用扩展IO：32pin
音视频/显示： 7段数码管：x8 VGA视频输出接口 Audio音频接口
通信接口：UART：USB转UART Bluetooth：蓝牙模块
模拟接口： DAC：8-bit分辨率 XADC：2路12bit 1Msps ADC

Ⅰ. 前置知识

0x00 利用D触发器构造环形计数器（自循环移位寄存器）

0x01 扭环形计数器（约翰逊计数器）

Ⅱ. Verilog实现：

0x00 环形计数器

0x01 扭环计数器

Ⅰ. 前置知识

0x00 利用D触发器构造环形计数器（自循环移位寄存器）

下图为利用D触发器构造的计数器电路，如果初始时将A、B、C、D置为1000，CP接单脉冲计数，则计数器可以实现one-hot计数。

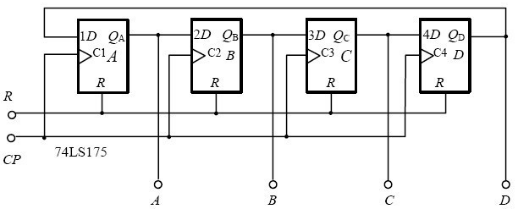
环形计数器原理

参考程序如下，

module circle_counter(rst_n, clk, cnt ); 
parameter CNT_SIZE = 8;
input rst_n;
input clk;
output [CNT_SIZE-1 : 0] cnt;
reg [CNT_SIZE-1 : 0] cnt;
always@(posedge clk)
    if(!rst_n)
        cnt <= 8'b0000_0001;  //初始值
    else
        cnt <= {cnt[0],cnt[CNT_SIZE-1 : 1]};//注意是循环移位，而非简单的移位
        //cnt <= cnt>>1;
Endmodule

在下图中，用74LS10的三输入端与非门修改上述电路，使得初始值0000启动时，下一个CP脉冲时计数器状态可以自行跳至1000。

请自行总结自启动的体会。（注意：74LS10有一个门起非门作用）

自启式环形计数器

参考程序如下：

module circle_counter(rst_n, clk, cnt ); 
parameter CNT_SIZE = 8;
input rst_n;
input clk;
output [CNT_SIZE-1 : 0] cnt;
reg [CNT_SIZE-1 : 0] cnt;
always@(posedge clk)
    if(!rst_n)
        cnt <= 8'b0000_0001;  //初始值
    else
        cnt <= {cnt[0],cnt[CNT_SIZE-1 : 1]};//注意是循环移位，而非简单的移位
        //cnt <= cnt>>1;
Endmodule

上面的代码仅仅是简单的实现，模拟环形计数器的工作方式，并没有过多的考虑自启动的问题。

对于环形计数器，功能上又被称作one-hot（独热码）计数器，优点是速度快，且每次只有两个bit发生跳变，而且不需外加译码电路，可以直接以各个触发器输出端的1状态表示计数。

主要缺点是没有有效利用电路的状态，对于n bit，有2n-n个状态没有利用。应用中，在状态机的状态编码时，经常用到此类计数器，如4bit one-hot计数器的计数序列即为：0001-0010-0100-1000循环。也因此，大多情况下这种计数器不被称作计数器，而是状态编码的一种。

若要设计可以自启动（自动从无效状态转移到有效状态，进入有效循环）的电路，可参考附加实验中状态机设计的实验内容，通过修改状态逻辑实现，本质是改变无效状态的次态，使其为有效状态。

0x01 扭环形计数器（约翰逊计数器）

基本原理：设置一个初始状态，将最高位取反，作为最低位的输入，通过移位即可得到。

如图：

扭环形计数器原理示意

参考代码：

module john_counter(rst_n, clk, cnt );
parameter CNT_SIZE = 4;
input rst_n;
input clk;
output [CNT_SIZE-1 : 0] cnt;
reg [CNT_SIZE-1 : 0] cnt;
always@(posedge clk)
    if(!rst_n)
        cnt <= 4'b0000 ;  //初始值
    else
        cnt <= {~cnt[0],cnt[CNT_SIZE-1 : 1]}; //注意是循环移位，而非简单的移位
endmodule

Ⅱ. Verilog实现：

0x00 环形计数器

设计代码：

module circle_counter(rst_n, clk, cnt ); 
parameter CNT_SIZE = 8;
input rst_n;
input clk;
output [CNT_SIZE-1 : 0] cnt;
reg [CNT_SIZE-1 : 0] cnt;
always@(posedge clk)
 if(!rst_n)
 cnt <= 8'b0000_0001; 
 else
 cnt <= {cnt[0],cnt[CNT_SIZE-1 : 1]};
endmodule

仿真代码：

module test();
reg rst_n,clk;
wire [7:0]cnt;
circle_counter uut(.rst_n(rst_n),. clk(clk),. cnt(cnt));
initial begin 
		clk = 'b0;
		rst_n = 'b0;
		# 10
		rst_n = 'b1;
        # 2000
                $finish;
            end
        
            always #5 clk = ~clk;
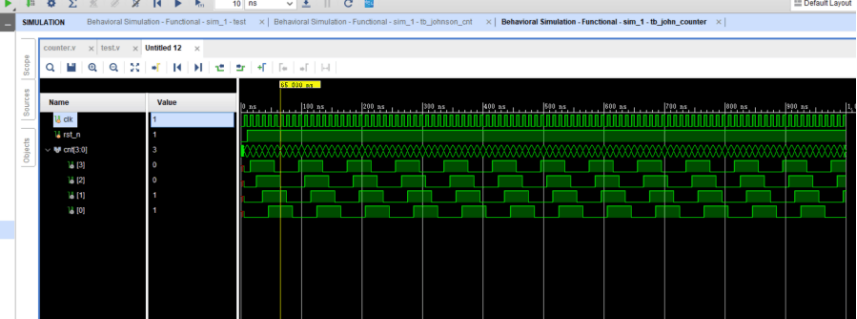
endmodule

仿真波形图：

0x01 扭环计数器

设计文件：

module john_counter(rst_n, clk, cnt );
parameter CNT_SIZE = 4;
input rst_n;
input clk;
output [CNT_SIZE-1 : 0] cnt;
reg [CNT_SIZE-1 : 0] cnt;
always@(posedge clk)
 if(!rst_n)
 cnt <= 4'b0000 ; 
 else
 cnt <= {~cnt[0],cnt[CNT_SIZE-1 : 1]}; 
 endmodule

仿真文件：

module tb_john_counter();
	reg clk, rst_n;
	wire [3:0] cnt;
john_counter uut(.rst_n(rst_n),. clk(clk),. cnt(cnt));
	initial begin 
		clk = 'b0;
		rst_n = 'b0;
		# 10
		rst_n = 'b1;
		# 2000
		$finish;
	end
	always #5 clk = ~clk;
Endmodule

仿真波形图：