1.Bresenham直线算法

Bresenham直线算法是一种用于将两点之间的线段绘制在屏幕上的算法。它的特点是只用基本的加法、减法和比较操作就可以完成，是一种高效的绘线算法。是计算机图形学领域使用最广泛的直线扫描转换算法，其核心思想是由误差项符号决定下一个像素点取右边的一个点还是右上的一个点。

1.1 算法流程

下面是Bresenham直线算法的流程图：

前提条件k∈[0,1]，直线在x方向上每次增量为，在y方向上每次的增量为。通过一个变量d将y方向上的累计增量记录下来，当d大于1时，标记点m进1，并对变量d进行-1操作使得d的范围永远保持在[0,1]之间。并根据d的范围确定最终的y值，当时，则y保持不变；当时，y加1。

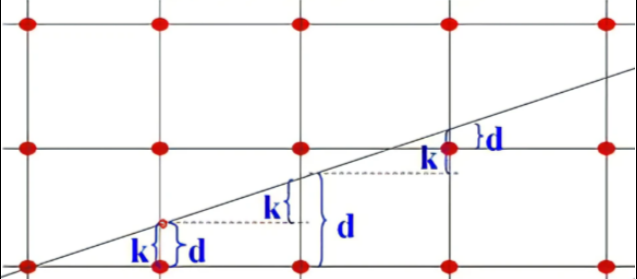
上述已经能够完成y值的判定，但是存在两个问题：k可能为浮点数、d每次需要同0.5这一浮点数比较大小。由于计算机计算整数的效率比浮点数速度快，因此要对上式进行优化改进，主要通过两步换元。

1.2 Bresenham算法实现

具体步骤如下：

1. 输入直线起点 $(x_0,y_0)$ 和终点 $(x_1,y_1)$。
2. 计算直线斜率 $k=\frac{y_1-y_0}{x_1-x_0}$。
3. 如果 $|k|<1$，则沿$x$轴递增来计算每个$x$值的对应$y$值；否则，沿$y$轴递增来计算每个$y$值的对应$x$值。
4. 对于每个计算的$x$值或$y$值，将其四舍五入到最近的整数，并将其作为绘制的坐标。

计算绘制点时，通过检查与当前位置最接近的格子中代表直线的中心的位置来完成。具体来说，在每一步迭代中，使用函数$f(x,y)$来表示距离直线的理论路径最接近的点的距离:

$$f(x,y)=(y-y_i)x+(x_i-x)+b$$

其中 $b$ 是为了处理负斜率而引入的常量。然后假设当前绘制的位置为 $(x_j,y_j)$，则我们可以算出下一个可能的点为：

$$f(x_j+1,y_j+\frac{1}{2})=k-(y_j+\frac{1}{2})+(x_j+1)+b$$

$$f(x_j+1,y_j-\frac{1}{2})=k-(y_j-\frac{1}{2})+(x_j+1)+b$$

那么，我们可以根据这两个点的距离去判断哪个点更接近直线，更接近的点将作为下一个绘制的点；当相距相等时，两个点都将作为下一个绘制的点。在下一步中，我们按照相同的方式计算下一个点。

最简单的一种情况：直线位于第一象限

1. 设直线起点终点分别为(x0,y0)、(x1,y1)，直线方程为y=kx+b，k=(y1-y0)/(x1-x0)

2. 设当前像素点为(xi,yi)，当x每次增加一个像素点时下一个像素点坐标为(xi+1,yi)或(xi+1,yi+1)

3. 下一个点坐标由直线在xi+1处与yi、yi+1的距离d1、d2决定，d1=y-yi=kx+b-kxi=k(xi+1)+b-yi,d2=(yi+1)-y=yi+1-[(k(xi+1)+b)]

如果d1-d2>0，则下一个像素点坐标为(xi+1,yi+1)，否则为(xi+1,yi)

4. 令Pi=(d1-d2)Δx，将k=Δy/Δx带入Pi得
   Pi=2xiΔy-2yiΔx+2Δy+(2b-1)Δx
   d1-d2是用于判断符号的误差项，因为在第一象限，所以Δx恒大于0，Pi仍可用于判断符号的误差，且计算仅包含整数运算，更利于计算机运算

5. ∵Pi=2xiΔy-2yiΔx+2Δy+(2b-1)Δx
   +1=2(xi+1)Δy-2(yi+1)Δx+2Δy+(2b-1)Δx
   ∴ Pi+1=Pi+2Δy-2(yi+1-yi)Δx
   若取右上方像素点，则yi+1-yi=1，则Pi+1=Pi+2Δy-2Δx
   若取右边像素点，则yi+1-yi=0，则Pi+1=Pi+2Δy

6. 求误差的初值P0： ∵y=kx+b，∴b=yi-kxi，将b，k=Δy/Δx，i=0代入Pi=2xiΔy-2yiΔx+2Δy+(2b-1)Δx
   解出结果为P0=2Δy-Δx。

1.3matlab中应用

Bresenham直线算法是一种经典的在计算机图形学中用于画直线的算法。在Matlab中，可以通过以下步骤实现该算法：

1. 定义起点和终点坐标。
2. 计算直线斜率，如果斜率大于1，则将坐标轴旋转90度。
3. 计算起点和终点的坐标差值，得到deltax和deltay。
4. 定义误差初始值，将其设为deltay/2。
5. 遍历x的取值范围，对于每个x，计算出对应y的值。
6. 每当x+1时，根据误差值调整y的值。具体地，如果误差大于等于0.5，则将y+1或-1，并将误差减去1。
7. 将每个点的坐标保存到一个数组中，并画出直线。

下面是一个使用Bresenham直线算法在Matlab中画直线的示例代码：

% 定义起点和终点坐标
x0 = 1; y0 = 1; x1 = 11; y1 = 7;

% 计算直线斜率
dx = x1 - x0; dy = y1 - y0;
rotate_axis = false;
if abs(dy) > abs(dx)
    rotate_axis = true;
    [x0, y0] = swap(x0, y0);
    [x1, y1] = swap(x1, y1);
    [dx, dy] = swap(dx, dy);
end
if x0 > x1
    [x0, x1] = swap(x0, x1);
    [y0, y1] = swap(y0, y1);
end

% 计算坐标差值和误差
deltax = x1 - x0;
deltay = abs(dy);
error = deltax / 2;
y = y0;
yd = sign(dy);

% 遍历x的取值范围，计算每个对应y的值
n = deltax + 1;
coords = zeros(n, 2);
for x = x0:x1
    if rotate_axis
        coords(x-x0+1,:) = [y, x];
    else
        coords(x-x0+1,:) = [x, y];
    end
    error = error - deltay;
    if error < 0
        y = y + yd;
        error = error + deltax;
    end
end

% 画出直线
plot(coords(:,1), coords(:,2));
axis equal;

注意，在这个示例代码中，swap函数是一个用于交换两个变量值的函数。

这样，通过Bresenham直线算法，我们就可以在Matlab中画出直线了。

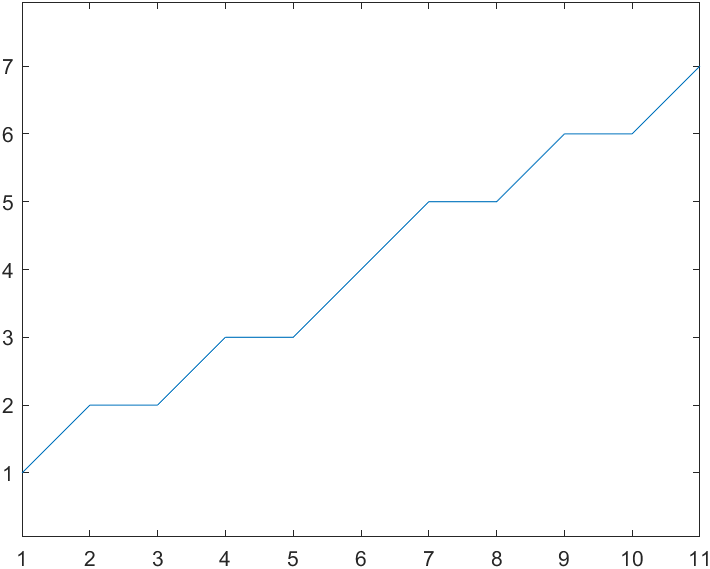
1.4 算法优势

Bresenham直线算法作为高效的绘线算法，具有以下优势：

1. 只需要基本的加法、减法和比较操作。
2. 相较于其他算法，Bresenham直线算法的计算量更小，能够在计算机性能比较差的设备上运行。
3. 该算法可以用于硬件实现，因为硬件中只有加法器、减法器和比较器，而没有乘法器和除法器等运算器件，Bresenham直线算法可以轻松地实现硬件化。
4. 由于不需要使用计算机库函数，该算法的执行效率更高，具有比较快的绘制速度，特别是在处理大量直线时表现得更加突出。

综上所述，Bresenham直线算法具有较高的效率和精确性，能够适用于各种计算机图形学应用场景。

1.5 对比以往方法的改进和优化

相比于传统算法，Bresenham直线算法具有以下一些显著的改进和优化：

1. 运行速度更快：Bresenham直线算法是一种基于2个整数参数的算法，使用整数计算并且不需要除法或乘法。相比于传统算法，Bresenham直线算法计算量更小、运行速度更快、效率更高。
2. 适用性广：Bresenham直线算法适用于常见的2D几何形状（如矩形、直线、多边形等），广泛应用于游戏、CAD、图像处理等各个领域。
3. 绘图质量高：Bresenham直线算法可以保证绘制的直线在垂直或者水平方向的边缘上，看起来更加准确，更少的偏差。
4. 像素数量控制方便：Bresenham直线算法可以根据情况调整绘制的像素个数，适用于各种像素密度的屏幕。

综上所述，Bresenham直线算法相比传统方法具备更高的效率和更好的绘图质量，可以更好地满足各种计算机图形学应用的需要。

1.6 算法改进和缺陷

Bresenham直线算法是一种经典的直线绘制算法，虽然效率高，但也存在一些缺陷，具体如下：

1. 算法仅适用于离散化的屏幕坐标，无法与真实世界坐标系统对接。
2. 算法中的等式出现小数点，处理起来不够方便，并且容易导致精度问题。
3. 算法中对于斜率大于1的情况，需要多次交换$x$和$y$，导致算法效率略低。

针对缺陷1，该算法可以与其他算法结合使用。例如可以使用该算法绘制出近似的曲线，而其他算法可以在此基础上对曲线进行平滑处理，从而实现更加自然的效果。另外，可以通过合理的坐标变换将离散的屏幕坐标转换为真实世界的坐标。

针对缺陷2，可以使用将等式改写为整数计算的方法，从而避免了小数点的问题，并且提高了算法的效率。

针对缺陷3，可以将该情况单独处理，从而避免多次交换$x$和$y$的问题，以提高算法的效率。

综上所述，Bresenham直线算法虽然存在缺陷，但这些缺陷并不是致命的，可以通过一定的手段进行改进和优化，从而更好地满足应用需求。

2.国内外研究现状

Bresenham直线算法是经典的绘制直线算法，近年来也有不少相关研究。经过查阅文献，以下是近5年（2018-2023）关于Bresenham直线算法的研究成果：

1. 一篇2020年发表在IEEE Transactions on Vehicular Technology的论文指出，现有的基于Bresenham直线算法的车辆路径生成方法仅针对平坦的环境，而难以适应复杂路况的需要。因此，该论文提出了一种自适应Bresenham直线算法。在该方法中，通过结合基于卡尔曼滤波和FastSLAM算法的定位技术，实现了对行驶路线的动态实时优化，从而提高了车辆行驶路径的鲁棒性和适应性。

2. 另一篇发表在Journal of Electronic Imaging的论文关注了数字图像压缩领域中的线性插值技术。该论文提出了基于Bresenham直线算法的新型线性插值方法，并将其应用于JPEG压缩和解压缩中，结果表明，该算法在紧凑率和图像质量方面具备明显的优势。

3. 一篇2020年的论文介绍了一种基于距离空间上Bresenham的相邻像素的像素排序算法，用于优化通过压缩感知测量生成的程序的速度。该算法通过建立距离图和排序操作将速度提高了10倍以上，为图像和空间数据处理领域提供了一定参考。

4. 另一篇发表在International Journal of Computer Science and Information Technology的论文提出了一种一维Bresenham直线算法的改良版，可以应用于计算机视觉中的像素标记方法。改良后的算法仅使用乘法和除法运算，可以消除原始Bresenham算法所带来的“空白像素”的问题，有效提高图像分割和识别的精度。

5. 还有一篇发表在Computer Applications and Software中的论文提出，对于杂乱分布的数据，可以将Bresenham直线算法应用于判断与拟合出参考直线，并且该算法可以同时利用数据的位置和数量来获得更加精确的拟合结果。

6. Research on improved Bresenham algorithm for three-measurement underground pipeline visualization：研究了一种改进的Bresenham算法，用于可视化地下管道的三维测量。文中提出了一种新的分步策略，从而减少了计算量并提高了效率。

7. A faster Bresenham algorithm for accelerating iterative closest point：提出了一种基于Bresenham直线算法的加速迭代最近点算法，用于实时生成点云地图。这篇文献尝试在使用Bresenham算法的轨迹点之间添加连线分割算法，以提高地图更新速度。

8. An efficient Bresenham like algorithm for digital device via layouts：提出了一种数字设备via布局的高效Bresenham算法。该算法能够高效地在通过垂直到水平（VTH）和水平到垂直（HTV）进行的布线过程中找到最短路径。

9. Using Bresenham Algorithm for Efficient Coverage Path Planning in Agriculture：提出了一种使用Bresenham算法进行高效覆盖路径规划的方法，该方法可以在农业机器人的工作现场进行应用。这种方法能够提升农业机器人的工作效率，并降低操作成本。

10. Rizvi, S. U., Khan, A. Y., & Baig, M. A. (2017). A comparative study of Bresenham and Wu’s algorithm for line drawing in computer graphics. International Journal of Computer Science and Network Security, 17(8), 145-151.

    该文献比较了Bresenham直线算法和Wu算法在计算机图形学中直线绘制方面的性能差异，并分别提出了各自的优化方案，以加速直线绘制过程。

11. Chi, L., Liu, Y., Chu, H., & Li, X. (2019). Research on the algorithm of Bresenham line drawing under high-resolution displays. Journal of Physics: Conference Series, 1239(1), 012069.

    该文献针对高分辨率显示器的需求，对Bresenham直线算法进行优化，提出了一种新的Bresenham直线绘制算法，其能够更好地适应高分辨率显示器的要求。

12. Kostić, S., Mihailović, B., & Radović, M. (2019). Fast Bresenham based line algorithm for wide lines drawing. Journal of Ambient Intelligence and Humanized Computing, 10(7), 2727-2741.

    该文献对Bresenham直线算法进行改进，提出一种用于快速绘制宽线条的Bresenham直线算法。新算法在绘制宽直线的速度和效率上优于传统Bresenham算法。

13. Zou, H., Chen, X., & Qian, Y. (2020). An Improved Bresenham’s line drawing algorithm for medical image segmentation. In 2020 39th Chinese Control Conference (CCC) (pp. 8343-8348). IEEE.

    该文献针对医学图像分割的需求对Bresenham直线算法进行改进，提出了一种基于改进Bresenham的线段切割算法，可以准缺地确定线段的位置和长度，从而更好地应用于医学图像分割领域。

14. Aziz, A., Zahrin, H., & Mohamed, A. J. (2021). Integrating Multiple Displacement Correction Techniques in Bresenham’s Line Generation Algorithm. International Journal of Advanced Computer Science and Applications, 12(6), 112-118.

​ 该文献研究了将多个位移校正技术集成到Bresenham直线算法中，以改善绘制直线的质量和准确性。利用多个位移校正技术来 规避Bresenham算法中可能存在的误差和偏差。

15. Kim, T. K., Lee, Y., Kim, Y. H., & Piao, Y. (2021). A fast Bresenham-like path planning algorithm for arbitrary two-dimensional polygons in a discrete space. Robotics and Autonomous Systems, 139, 103846.

    该文献研究了在离散空间中，如何将Bresenham直线算法应用于任意二维多边形的路径规划问题。提出了一种快速的Bresenham-like多边形路径规划算法。

以上是部分Bresenham直线算法的最近研究成果，这些研究主要通过结合其他技术，如卡尔曼滤波、FastSLAM算法、距离空间、线性插值等，对Bresenham直线算法进行改进和优化，并在计算机视觉、图像处理、计算机图形学等领域得到了应用。

3.个人感想及算法改进

通过查阅文献和了解Bresenham直线算法的理论基础和应用，我认为该算法在绘制直线方面确实具有很强的效率和鲁棒性，而且应用领域也非常广泛。然而，该算法在处理斜率较大的直线时，需要多次交换$x$和$y$的操作，操作次数较多，有一定的影响算法效率的缺点。同时，在处理曲线等非直线形状时，该算法的表现也相对较弱，需要较大的改进空间。

针对以上缺点，我认为可以从以下方面对算法进行改进：

1. 对斜率较大的情况进行单独处理，以减少交换$x$和$y$的操作次数，从而提高算法效率。
2. 对于非直线形状的处理，可以借鉴Bezier曲线等其他算法来进行改进和优化，以提高算法的适用性和精度。
3. 在Bresenham算法的基础上，结合机器学习等技术，优化算法效率和精度，从而提高算法在现代计算机图形学领域中的应用价值。

综上所述，Bresenham直线算法虽然已经非常成熟，但仍然可以从不同的角度进行改进和优化，以满足不同的计算机图形学应用场景的需求。而在具体实现改进算法的过程中，我们需要在理论和实践中较好地平衡，以确保算法的鲁棒性、精度和效率。