数据结构：二叉树经典例题（单选题）--＞你真的掌握二叉树了吗？（第一弹）

news2024/9/17 8:31:44

朋友们、伙计们，我们又见面了，本期来给大家解读一下有关二叉树的经典例题，如果看完之后对你有一定的启发，那么请留下你的三连，祝大家心想事成！

C 语言专栏：C语言：从入门到精通

数据结构专栏：数据结构

个人主页：stackY、

前言：

一、

二、

三、

四、

五、

六、

七、

八、

九、

前言：

前面我们讲了二叉树的顺序结构和二叉树的链式结构，将二叉树的基本知识和实现过程都了解了一遍，那么本期我们来看看关于二叉树的经典例题都有哪些，在此之前，我们需要了解二叉树的性质，那么话不多说，我们直接开始！！！

一、

1. 在用树表示的目录结构中，从根目录到任何数据文件，有（）通道

A.唯一一条

B.二条

C.三条

D.不一定

题解： A

树的特点是不相交，所以不可能有多个路径同时到达一个点。

二、

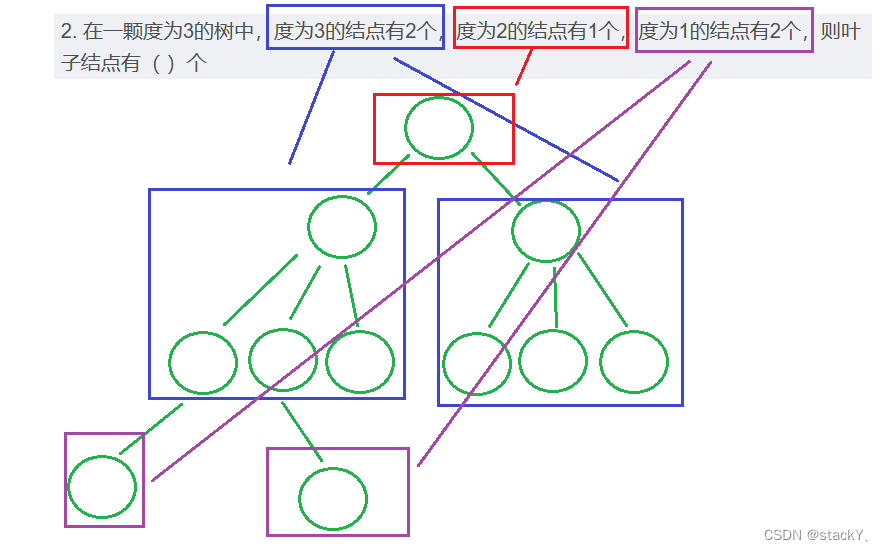
2. 在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（）个

A.4

B.5

C.6

D.7

题解： C

设度为i的节点个数为ni, 该树总共有n个节点,则n=n0+n1+n2+n3.

有n个节点的树的总边数为n-1条.

根据度的定义,总边数与度之间的关系为：n-1=0*n0+1*n1+2*n2+3*n3.

联立两个方程求解,可以得到n0 = n2 + 2n3 + 1, n0=6

或者可以通过画图来解答：

三、

3. 一颗拥有1000个结点的树度为4，则它的最小深度是（）

A.5

B.6

C.7

D.8

题解： B

如果这棵树每一层都是满的，则它的深度最小，树的度为4，那么假设它为一个四叉树，高度为h，则这个树的节点个数为(4^h - 1) / 3，当h = 5, 最大节点数为341，当h = 6, 最大节点数为1365，所以最小深度应该为6。

四、

4. 下列关于二叉树的叙述错误的是（）

A.二叉树指的是深度为 2 的树

B.一个 n 个结点的二叉树将拥有 n-1 条边

C.一颗深度为 h 的满二叉树拥有 2^h-1 个结点（根结点深度为1）

D.二叉树有二叉链和三叉链两种表示方式

题解： A

A错误: 二叉树指最大孩子个数为2，即树的度为二的树。深度描述的为树的层数。

B正确: 对于任意的树都满足：边的条数比节点个数少1，因为每个节点都有双亲，但是根节点没有

C正确: 正确，参照二叉树的性质

D正确: 二叉链一般指孩子表示法，三叉连指孩子双亲表示法，这两种方式是二叉树最常见的表示方式，虽然还有孩子兄弟表示法，该中表示方式本质也是二叉链

五、

5. 一颗完全二叉树有1001个结点，其叶子结点的个数是（）

A.251

B.500

C.501

D.不能确定

题解： C

该题需要用到二叉树性质：在任意二叉树中，度为0的节点都比度为2的节点多1个，即 n0 = n2 + 1另外，在完全二叉树中，如果节点总个数为奇数，则没有度为1的节点，如果节点总个数为偶数，只有一个度为1的节点。

因此：n0 + n1 + n2 = 1001 节点总数为奇数，没有度为1的节点

n0 + 0 + n2 = 2*n0-1 = 1001 n0 = 501

六、

6. 在一颗完全二叉树中，某一个结点没有其左孩子，则该结点一定（）

A.是根结点

B.是叶结点

C.是分支结点

D.在倒数第二层

题解： B

完全二叉树中如果一个节点没有左孩子，则一定没有右孩子，必定为一个叶子节点，最后一层一定为叶子节点，但是倒数第二层也可能存在叶子节点。

七、

7. 设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树中总的结点数为（）个

A.11

B.12

C.13

D.14

题解： C

设Ni表示度为i的节点个数，则节点总数 N = N0 + N1 + N2

节点个数于节点边的关系： N个节点的树有N-1个边

边与度的关系：N - 1 = N1 + 2 * N2

故：N0 + N1 + N2 - 1 = N1 + 2 * N2

因此，得：N0 = N2 + 1

回到原题，N0 = 3，N1 = 8，可得N2 = 2。

因此答案是 3 + 8 + 2 = 13。

八、

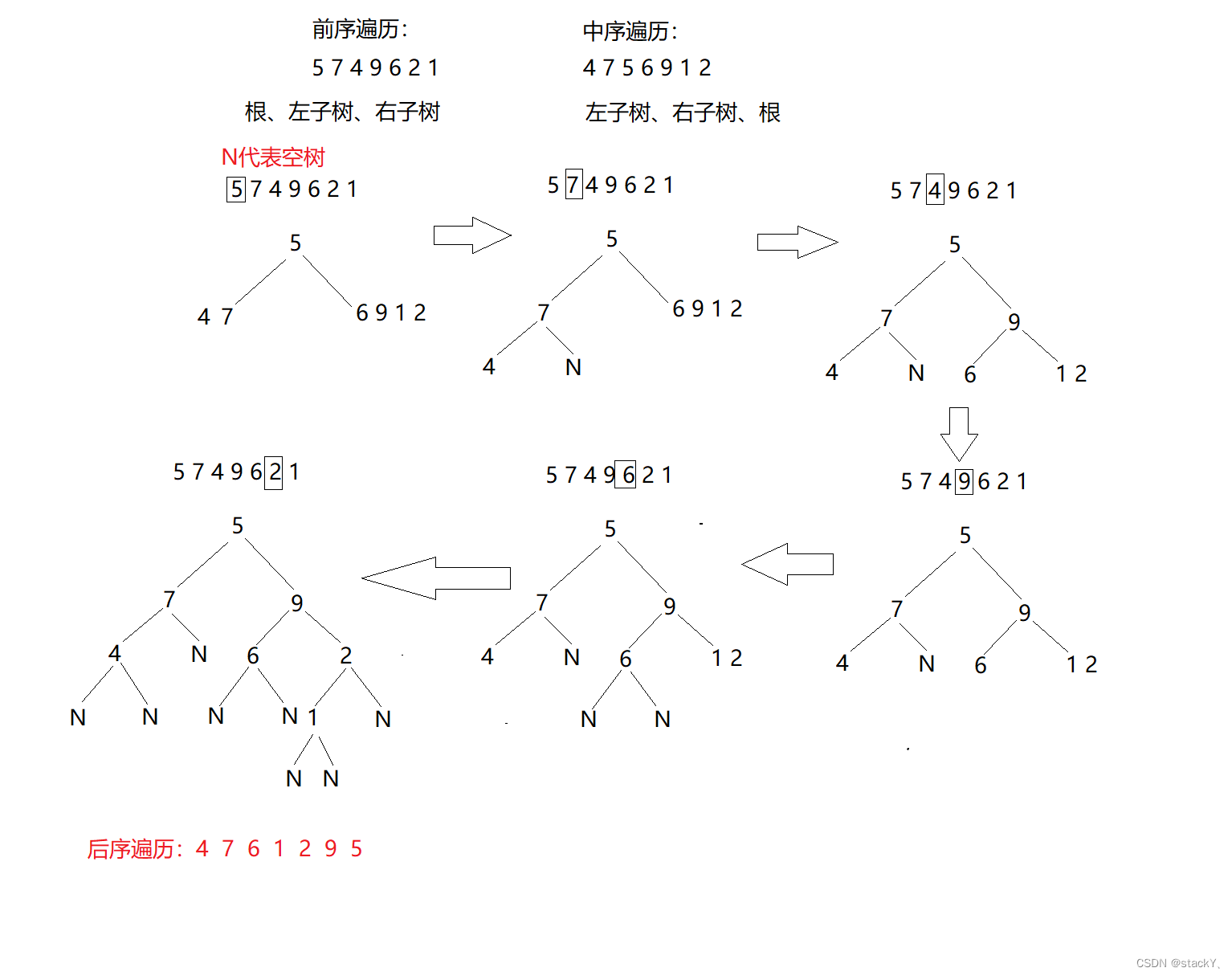
8. 已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，则其后序遍历序列为（）

A.4 2 5 7 6 9 1

B.4 2 7 5 6 9 1

C.4 7 6 1 2 9 5

D.4 7 2 9 5 6 1

题解： C

要知道后序遍历首先得将二叉树的结构还原出来，由于前序遍历首先访问的是根节点，所以5是根节点，然后在中序遍历的结果中找到5，5的左边就是一根节点为5的一颗左子树，右边就是一颗右子树，然后再找7，7的右边和左边又是两颗树，依次类推：

故：根为： 5

5的左子树：4 7   5的右子树： 6 9  1  2

5的左子树的根为: 7  5的右子树的根为：9

7的左子树: 4 7的右：空  9的左子树：6  9的右子树：2

故这棵树的结构为：

九、

9. 已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（）

A.ABDGHJKCEFILM

B.ABDGJHKCEILMF

C.ABDHKGJCEILMF

D.ABDGJHKCEIMLF

题解： B

由后序遍历确定子树的根，后序遍历从后向前看，最后一个元素为根，和前序遍历刚好相反，从后向前看后序遍历，应该是根，右，左，根据中序遍历确定子树的左右区间

故：根为: A

A的左子树：JGDHKB       A的右子树：ELIMCF

A的左子树的根：B        A的右子树的根：C

B的左子树：JGDHK  B的右子树：空  C的左子树：ELIM C的右子树：F

B的左子树的根：D         C的左子树根：E

D的左子树的根：G D的右子树的根：H  E的右子树的根:I

故树的结构为：