💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:八大排序专栏⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你学习排序知识
  🔝🔝

---

---

1. 前言

我们已经学过的:
插入排序,希尔排序,选择排序,堆排序
快速排序等等都是比较排序
也就是需要通过数据的比较来进行排序

而这里的计数排序比较特殊
它用的是一一对应的映射关系
它不用比较数据就能排好序

本篇文章分享的是:
计数排序思路以及代码全解

---

2. 计数排序基本思路

基本思路:

• 找出数组中的最大值和最小值
• 动态开辟一个空间
• 元素个数为最大值-最小值+1
• 再统计数据出现的次数

先定义一个无序数组:

int a[]={2,5,3,0,2,3,0,3};

此情况的分析:

1. 数组最大值为5,最小值为0
2. 开辟6个空间,统计数据出现的次数
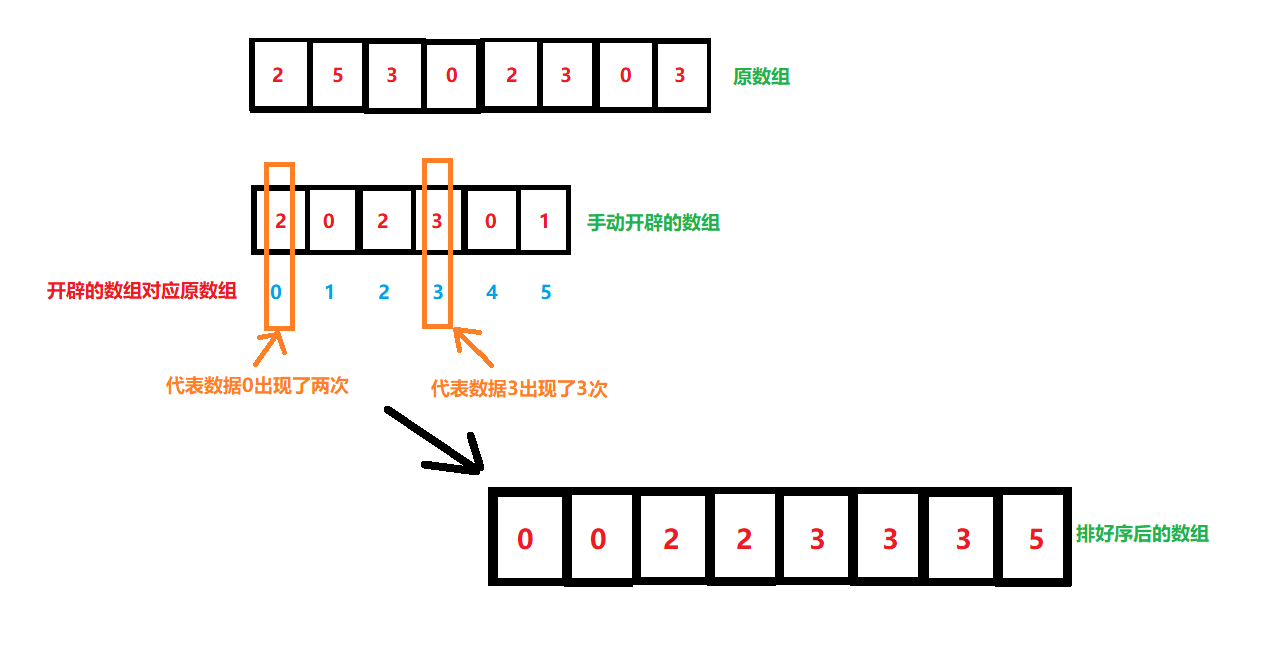
3. 开辟的数组中:
4. 第一个元素对应的是最小值0的个数
5. 最后一个元素对应的是最大值5的个数
6. 中间的1,2,3,4不管原数组有没有都写上
7. 统计完后重新导入原数组

画图理解:

---

3. 特殊情况分析

 
特殊情况:最小值为0

上面举例说明中,最小值是0.
所以开辟的数组中:
下标为0的位置对应数据0的个数
下标为5的位置对应数据5的个数
 

当最小值不为0时:

假设我们再定义一个数组:

int a[]={1000,1200,1001,1500,1300,1301};

1. 最大值为1500,最小值为1000
2. 开辟一个长度为1500-1000+1=501的数组
   (注意:长度为501的数组下标范围为0~500)
3. 我们把开辟的数组称为数组b
4. 此时b下标为0的点对应数据1000
5. b下标为501的点对应数据1500的个数

以此我们得出一个结论:

待排序数组中的元素X
映射到数组b的X-min的位置

 
画图理解:

---

4. 计数排序代码实现

我们分步骤来实现:

1. 函数参数以及返回值:

//计数排序
void CountSort(int* a, int n)
{
	//...
}

2. 找最值:

	int max = a[0];
	int min = a[0];
	//找最值
	for (int i = 1; i < n; i++)
	{
		if (max < a[i])
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;//动态开辟数组的元素个数
	int* count = (int*)calloc(range, sizeof(int));//将元素初始化为0

2. 计数:

//计数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
		//计数是去原数组中计数
	    //所以循环次数是n
	}

3. 根据次数进行排序:

	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)//只要count数组中元素不为0就赋值到原数组
		{
			a[j++] = i + min;
		}
	}
	free(count);//用完后释放空间
	count = NULL;

---

5. 计数排序缺陷

问题:

当数组中出现负数时.
比如:

int a[]={0,5,3,3,-1,2,0};

最小值是-1,最大值是5
这时开辟5-(-1)+1=7个空间有问题
 
解决方法:

我们知道-1的补码是:(32位机器下)
11111111111111111111111111111111

只需要将 -1 看作是一个无符号数
即:11111111...的无符号数是
十进制的: 4,294,967,295.

这时这个数组变成了
最大值为4,294,967,295
最小值为0.
开辟4,294,967,296个空间
进行计数排序

 
总结:

• 计数排序适合数据比较集中的数组
• 范围较大,有负数或者浮点数就不适合了

---

6. 计数排序复杂度分析

1. 时间复杂度分析:

一共有三个板块:

• 选最值.时间复杂度: O(N)
• 计数.时间复杂度: O(N)
• 排序.时间复杂度: O(Range)

注:N代表原数组长度.
range代表动态开辟数组长度

计数排序总时间复杂度:

O( Max(N , Range) )

2. 空间复杂度分析:

开辟了一个大小为Range的空间

空间复杂度为:
O (Range)

---

7. 总结以及拓展

终于!
八大排序全部结束!

插入排序,希尔排序,选择排序,堆排序
冒泡排序,快速排序,归并排序
和本节讲的计数排序.
在实际生活中都有很多运用
并且在面试时排序是必考的内容!

要熟练掌握啊!
完结撒花!

当然,排序部分还有稳定性
各大排序的比较,与实际运用
这最后一步放在下一章讲解

---

🔎 下期预告:八大排序总结分析 🔍