D分离（D-Separation）是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法，D-Separation更加直观，且计算简单。对于一个DAG（有向无环图）E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

 概念：很多的机器学习模型都可以用概率的角度去解释，其中一类重要的模型就是概率图模型，而是概率图模型的灵魂就是模型变量间的条件独立性。 因为有了独立性，才有了各种不同的概率图模型，比如LDA,HMM等等模型。在概率图中，变量间的独立性是怎么体现的呢？D-分离准则就是一种简单的技巧去判断一个概率图中的独立性的。

          简单的说，如果在概率图模型中，比如说X,Y两个节点没有边，使得X和Y之间肯定存在某种独立性，这种独立性可以是在某个子集Z的条件下使得他们独立，也可能是他们两个本身就是独立的，这时我们称X，Y之间是D-分离的。现在先给出D-分离的准则：

定义: 当路径p被结点集Z，d-分离（或被blocked掉）时，当且仅当以下条件成立：

①  若p包含形式如下的链i->m->j 或i<-m->j，则结点m在集合Z中。

②  若p中包含collider（碰撞点）i->m<-j,则结点m不在Z中且m的子代也不在Z中。

       更具体地讲，如果Z将X和Y d-separate，当且仅当Z将X，Y之间的每一条路径都block掉。

接下来逐步的介绍上述的准则，我们可以拆分成3个规则来考虑:

首先，这里我们先说明一下path，我们说两个结点之间的path的时候是不管他们之间边的方向的。

没有条件集的独立性

规则：如果x到y的任一path(路径)都经过collider(碰撞点)，则x和y独立。注意，这里的路径是忽略边的方向的，而碰撞点是指有多个箭头指向的它的节点，即类似于下图的A->B<-C

 head-to-head:A,C 独立

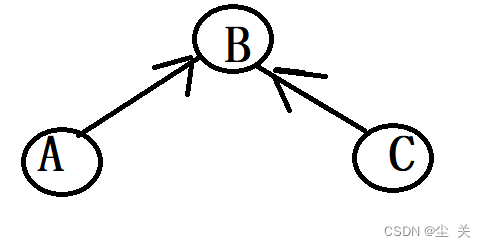
如果这个模型一旦在那里面见到了，认为他们是联通的，就认为他们是独立的，
但是如果它们的中心节点B 属于条件的一部分，那就和他们的原先属性相反了，他们就是不联通的
就变成了有独立性的了。

 规则2：当x到y的之间的任一路径都经过Z中的节点，且Z并不包含碰撞点或碰撞点的子代，则x和y独立。

tail-to-tail：A<-B->C: A,C并不独立

 

 

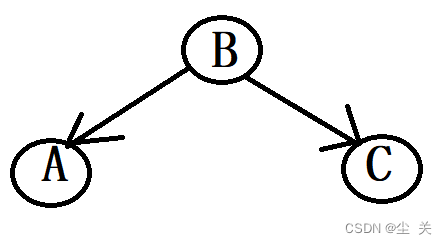
 head-to-tail ：A->B->C：A、C并不独立

 

注意， 如果这两个模型一旦在那里面见到了，就认为他们是联通的，即认为他们是不独立的，
但是如果它们的中心节点B 属于条件的一部分，那就和他们的原先属性相反了，他们就是不联通的
就变成了有独立性的了。

实例：

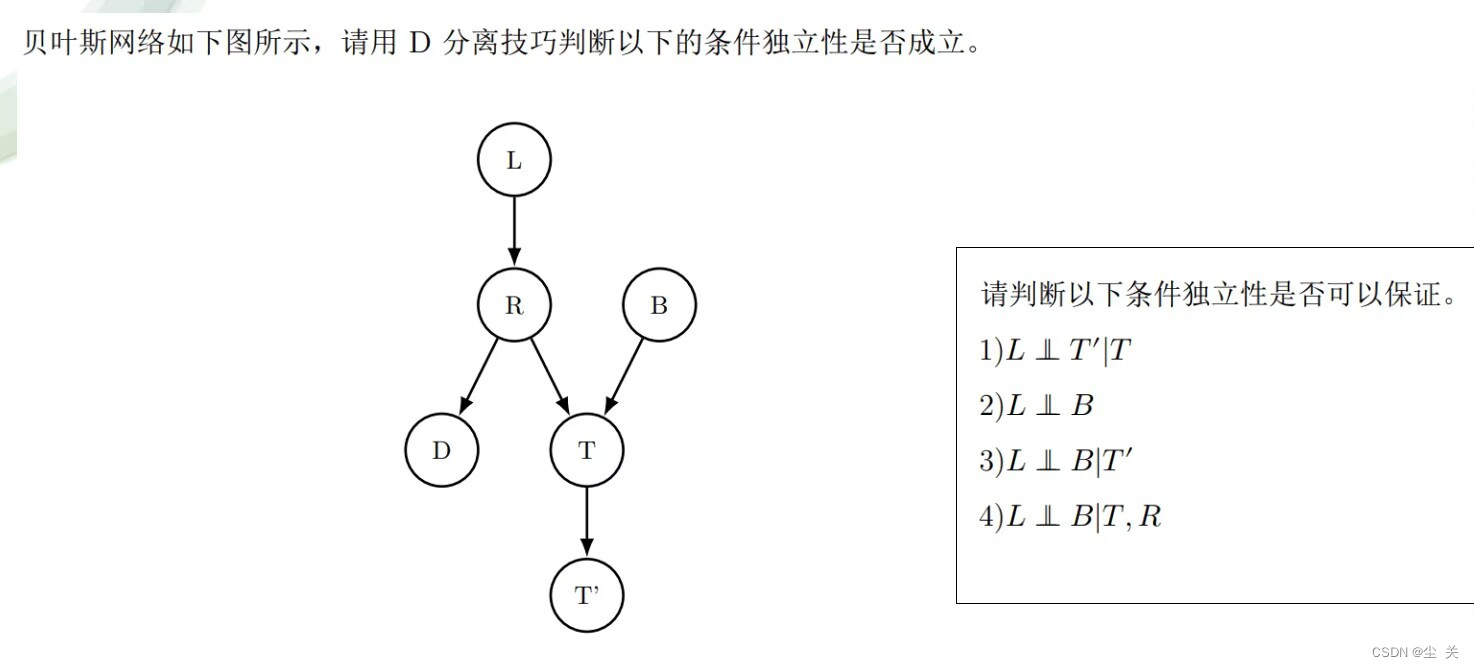
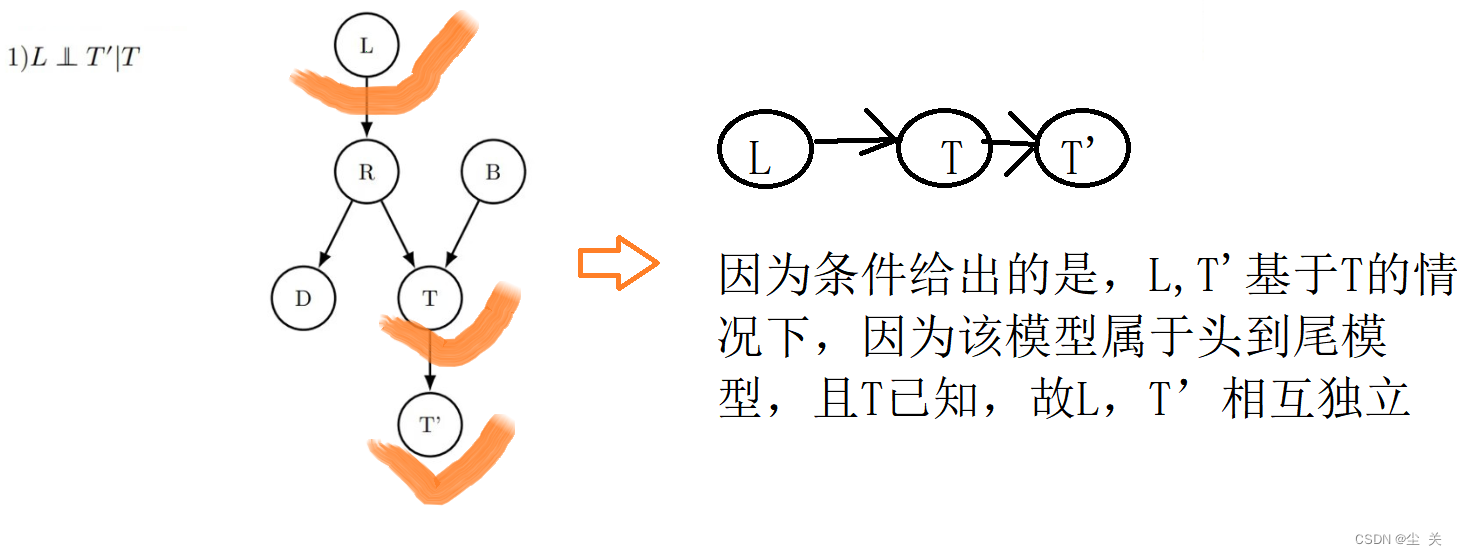
1. 

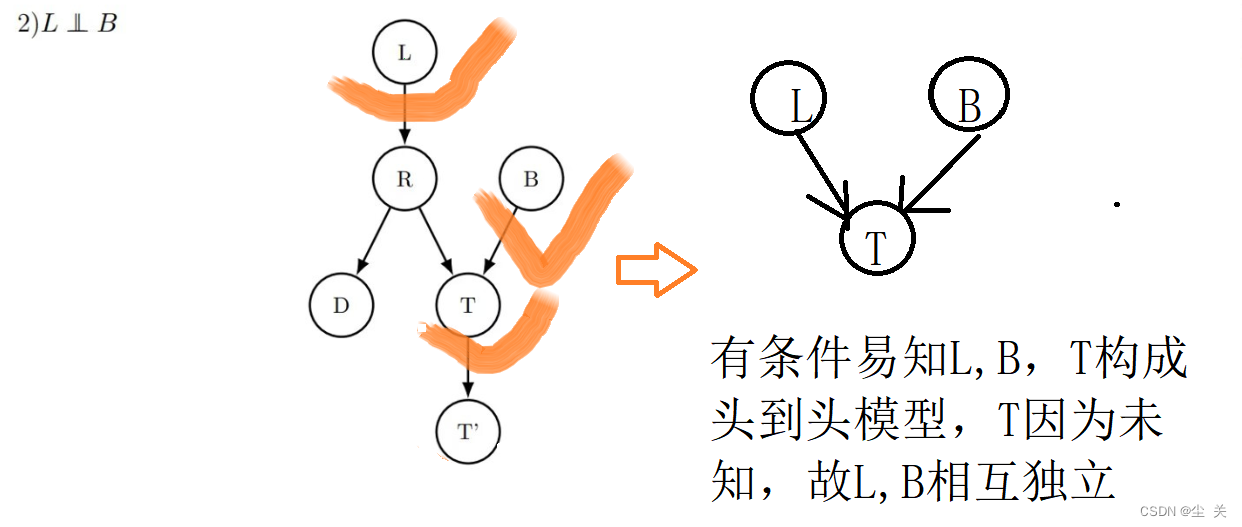
2. 

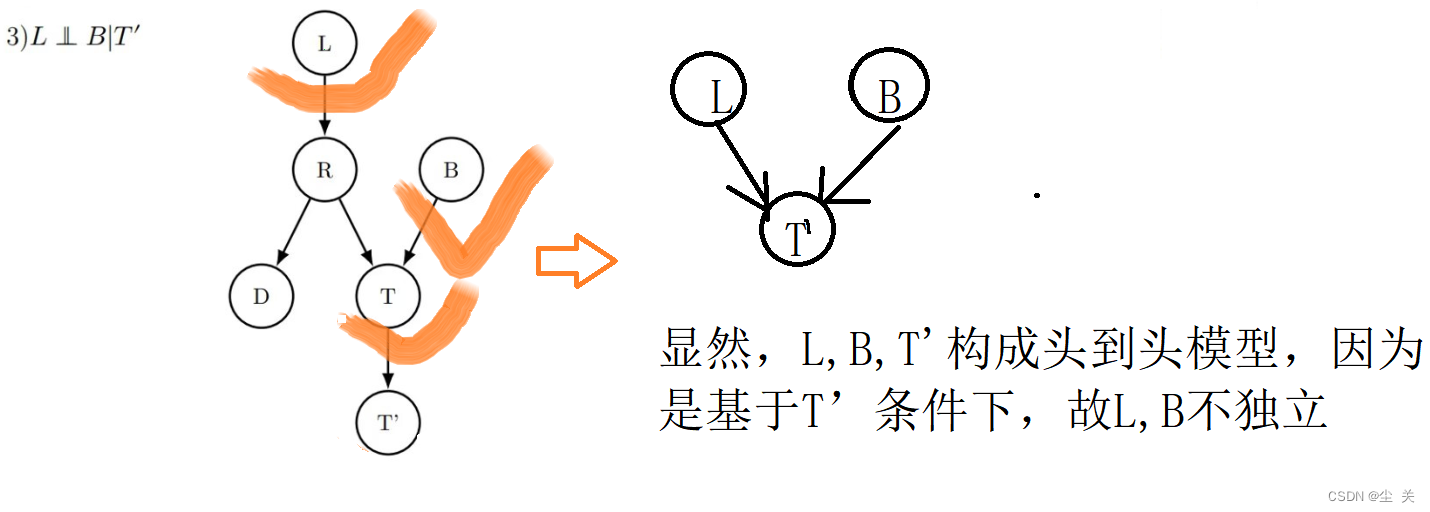
3. 

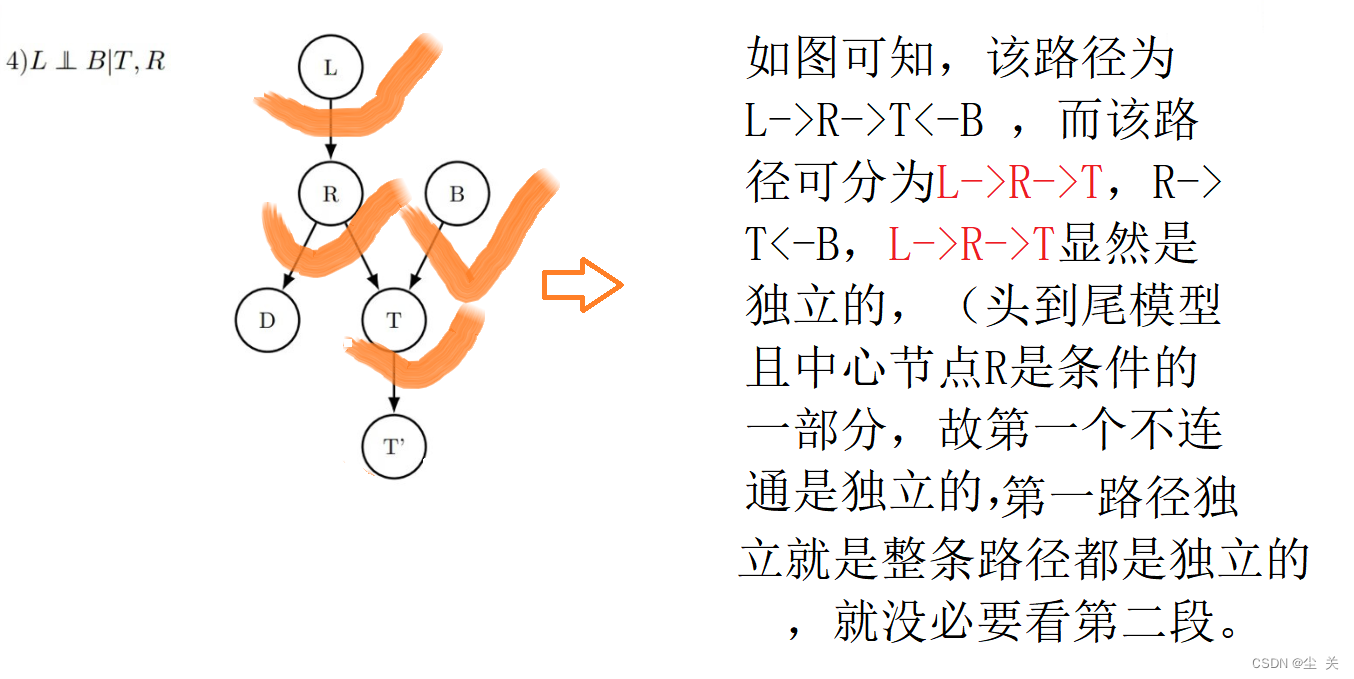
4.